8._德莫弗一拉普拉斯中心极限定理

德莫弗一拉普拉斯定理

假设随机变量服从二项分布，即 $Y_n \sim B(n, p)(0<p<1, n \geqslant 1)$ ，则对任意实数 $x$ ，有

这个被称为 德莫弗一拉普拉斯中心极限定理，也称为二项分布极限定理。 证明：略。

他表明，如果 $X \sim B(n, p)$ ，则当 $n$ 充分大时，有

如下图

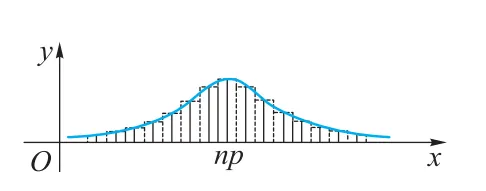
即当 $n \geqslant 30$ 时，其误差可以忽略不计．

棣莫弗-拉普拉斯中心极限定理，也称为二项分布以正态分布为极限分布的中心极限定理

注意： （1）如果记 $X_i \sim B(1, p)(0<p<1, i=1,2, \cdots)$ ，即 $X_i \sim\left(\begin{array}{cc}1 & 0 \\ p & 1-p\end{array}\right)$ 且相互独立，则

由列维—林德伯格定理推出棣莫弗—拉普拉斯定理。 （2）二项分布概率计算的三种方法． 设 $X \sim B(n, p)$ ．

①当 $n$ 不太大时 $(n \leqslant 10)$ ，直接计算

②当 $n$ 较大且 $p$ 较小时 $(n>10, p<0.1), \lambda=n p$ 适中，根据泊松定理有近似公式

③当 $n$ 较大而 $p$ 不太大时 $(p<0.1, n p \geqslant 10)$ ，根据中心极限定理，有近似公式

隶莫弗-拉普拉斯中心极限定理表明n重伯努利试验事件A出现的次数服从正态分布。

例某单位的局域网有 100 个终端，每个终端有 $10 \%$ 的时间在使用，如果各个终端使用与否是相互独立的．（1）计算在任何时刻同时最多有 15 个个终端在使用的概率；（2）用中心极限定理计算在任何时刻同时最多有 15 个个终端在使用的概率的近似值；（3）用泊松定理计算在任何时刻同时最多有 15 个终端在使用的概率近似值。

解 设随机变量 $X_i=\left\{\begin{array}{l}1, \text { 第 } i \text { 个终端在使用；} \\ 0, \text { 否则。 }\end{array}\right.$ $i=1,2, \cdots, 100$ ．由已知得 $X_1, \cdots, X_{100}$ 独立同分布 且 $X_i \sim B(1, p)$ 其中 $p=0.1$ ．同时使用的终端数 $\sum_{i=1}^{100} X_i B(100,0.1)$ ．

解 （1）借助于计算机得

即在任何时刻同时最多有 15 个终端在使用的概率为 0.9601 。 （2）因为 $E\left(\sum_{i=1}^{100} X_i\right)=100 \times 0.1=10, D\left(\sum_{i=1}^{100} X_i\right)=10 \times 0.9=9$ 。运用德莫弗一拉普拉斯中心极限定理 $\sum_{i=1}^{100} X_i \stackrel{\text { 近以 }}{\sim} N(10,9)$ ．因此

即在任何时刻同时最多有 15 个终端在使用的概率近似值为 0.9522 ．

（3）因为 $n>10, p<0.1$ ，所以 $\sum_{i=1}^{100} X_i \stackrel{\text { 近以 }}{\sim} P(10)$ ．有

即在任何时刻同时最多有 15 个终端在使用的概率近似值为 0.9513 ．

三大中心极限定理区别与应用

独立同分布的中心极限定理 $\left.\lim _{n \rightarrow \infty} P\left(\dfrac{\sum_{i=1}^n X_i-n \mu}{\sqrt{n} \sigma }\right) \le x \right)=\int_{-\infty}^x \frac{1}{\sqrt{2 \pi}} e ^{-\frac{t^2}{2}} d t=\Phi(x)$

棣莫弗－拉普拉斯定理 $\lim _{n \rightarrow \infty} P \left\{\dfrac{X-n p}{\sqrt{n p(1-p)}} \leqslant x\right\}=\int_{-\infty}^x \frac{1}{\sqrt{2 \pi}} e ^{-\frac{t^2}{2}} dt =\Phi(x)$

李雅普诺夫定理 $\lim _{n \rightarrow \infty} P\left\{\dfrac{\sum_{i=1}^n X_i-\sum_{i=1}^n \mu_i }{\sqrt{\sum_{k=1}^n \sigma_k^2}} \leqslant x \right\}=\int_{-\infty}^x \frac{1}{\sqrt{2 \pi}} e ^{-\frac{t^2}{2}} d t=\Phi(x)$

背景

首先，列维-林德伯格定理，也就是独立同分布的中心极限定理，适用于独立同分布的随机变量序列，只要期望和方差存在，标准化后的和趋近于正态分布。这个定理是中心极限定理中最经典的形式，应用广泛，比如在统计学中的大样本推断。

然后是棣莫弗-拉普拉斯定理，它其实是列维-林德伯格定理的一个特例，专门针对二项分布的情况。当试验次数n很大时，二项分布可以用正态分布来近似。这个定理在概率论早期由棣莫弗提出，后来拉普拉斯推广，所以名字是两个人的。

接下来是李雅普诺夫定理，属于独立不同分布情况下的中心极限定理。李雅普诺夫放宽了条件，允许随机变量不同分布，但需要满足李雅普诺夫条件，即存在某个δ>0，使得高阶矩的条件成立。这样，即使变量不同分布，只要满足条件，标准化后的和仍然趋近于正态分布。

核心条件与适用范围

应用场景对比