27._课外阅读_狄利克雷分布 - Probability Theory and Mathematical Statistics

应用背景：当你参加一个大型聚餐时，往往想去一桌人多的地方，也就是“聚集效应”；而自己去一张新的桌子的概率取决于“心情”( $\alpha$ ,比如可能要帮别人占位置，那么 $\alpha$ 较大，占新桌子的可能性也更大）

狄利克雷分布是一种＂分布的分布＂（a distribution on probability distribution），由两个参数 $\alpha, G_0$ 确定，即 $G \sim D P\left(\alpha, G_0\right), ~ \alpha$ 是分布参数（concentration or scaling parameter），其值越大，分布越接近于均匀分布，其值越小，分布越concentrated。 $G_0$ 是基分布（base distribution）。

我们可以通过图1来形象的理解DP，可以把DP想象成黑箱，输入分布 $G_0$ ，输出分布 $G$ ，而 $\alpha$ 控制输出的样子。

$图片$

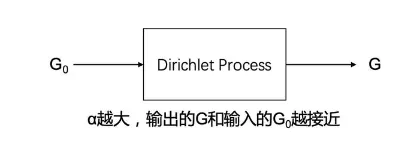
狄利克雷分布（Dirichlet distribution）是一个随机变量连续多元随机分布，它是贝塔分布的多元一般化。它的支集是 $\left\{\left(x_1, \cdots, x_K\right): x_i \in\{0,1\} \forall i \in\{1, \cdots, k\}, \sum_{i=1}^K x_i=1\right\}$ 。对于 $K \geq 2$ ，一个参数为 $\alpha=\left(\alpha_1, \cdots, \alpha_K\right) \in R _{++}^K$ 的 $K$ －阶狄利克雷分布随机变量的PDF是

我们有一组来源于混合高斯分布的数据集，希望对其进行聚类，然而我们并不知道这组数据是由几组高斯分布生成的（图1）。

$图片$

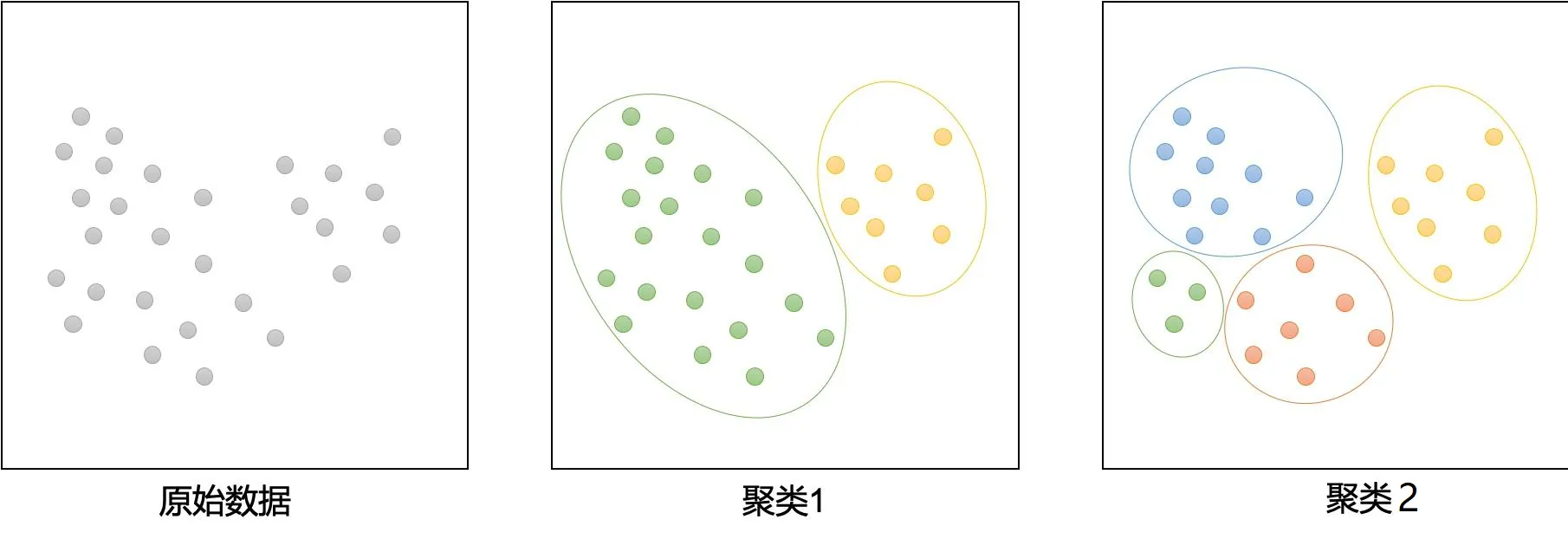
问题特点

（1）聚类数量未知

（2）非参数化，即不确定参数，如果需要，参数数量可以变化

（3）聚类数量服从概率分布

\begin{gathered} f\left(x_1, \cdots, x_K\right)=\frac{1}{B(\alpha)} \prod_{i=1}^K x_i^{\alpha_i-1} \\ B(\alpha)=\frac{\prod_{i=1}^K \Gamma\left(\alpha_i\right)}{\Gamma\left(\alpha_0\right)}, \alpha_0=\sum_{i=1}^K \alpha_i \\ \Gamma\left(\alpha_i\right)=\int_0^{\infty} t^{\alpha_i-1} e^{-t} d t \end{gathered}