2.2 酉等价 因为酉矩阵 U U U U ⋆ = U − 1 U^{\star} = U^{-1} U ⋆ = U − 1 U U U A → U ∗ A U A \to U^{*}AU A → U ∗ A U M M M
72
2.2.1 定义 设矩阵 A , B ∈ M n A, B \in M_n A , B ∈ M n U ∈ M n U \in M_n U ∈ M n B = U ∗ A U B = U^* A U B = U ∗ A U B B B A A A U U U B B B A A A
练习 证明西等价是一个等价关系.
2.2.2 定理 如果 A = [ a i j ] A = [a_{ij}] A = [ a ij ] B = ⌊ b i j ⌋ ∈ M n B = \lfloor b_{ij}\rfloor \in M_n B = ⌊ b ij ⌋ ∈ M n
∑ i , j = 1 n ∣ b j ∣ 2 = ∑ i , j = 1 n a j ∣ 2 . \sum_ {i, j = 1} ^ {n} \left| b _ {j} \right| ^ {2} = \sum_ {i, j = 1} ^ {n} a _ {j} \left| ^ {2} \right.. i , j = 1 ∑ n ∣ b j ∣ 2 = i , j = 1 ∑ n a j 2 . 证明:作矩阵乘法后便可看出 ∑ i , j ∣ a i j ∣ 2 = tr A ∗ A \sum_{i,j}|a_{ij}|^2 = \operatorname{tr}A^*A ∑ i , j ∣ a ij ∣ 2 = tr A ∗ A tr B ∗ B = tr A ∗ A \operatorname{tr}B^*B = \operatorname{tr}A^*A tr B ∗ B = tr A ∗ A B = U ∗ A U B = U^{*}AU B = U ∗ A U tr B ∗ B = tr U ∗ A ∗ U U ∗ A U = tr U ∗ A ∗ A U = tr A ∗ A . \operatorname{tr}B^*B = \operatorname{tr}U^*A^*UU^*AU = \operatorname{tr}U^*A^*AU = \operatorname{tr}A^*A. tr B ∗ B = tr U ∗ A ∗ U U ∗ A U = tr U ∗ A ∗ A U = tr A ∗ A .
练习 定理(2.2.2)说明 tr A ∗ A \operatorname{tr} A^{*} A tr A ∗ A A ∗ A A^{*} A A ∗ A
练习 证明
[ 3 1 − 2 0 ] 和 [ 1 1 0 2 ] \left[ \begin{array}{c c} {3} & {1} \\ {- 2} & {0} \end{array} \right] \quad \text {和} \quad \left[ \begin{array}{c c} {1} & {1} \\ {0} & {2} \end{array} \right] [ 3 − 2 1 0 ] 和 [ 1 0 1 2 ] 相似,但不西等价.
因为西等价蕴涵相似,但是反之不成立,所以,与相似等价关系相比,西等价关系把 M n M_{n} M n
计算逆容易得多,所以在计算上,西等价关系要比相似关系更简单。在出现舍入误差的情况下,它也能较好地保证精确性。因此,在数值计算中,它是可取的。关于这方面的细致理由就不在这里阐述了,但是,可以作一个直观的解释,那就是用一个酉矩阵做乘法有保持长度的性质。
下述两种特殊的(又很简单的)酉矩阵形式给出两种西等价变换,它们在特征值的计算中非常重要.
2.2.3 例:平面旋转 设 U ( θ ; i , j ) = [ 1 ⋱ 0 1 … cos θ 0 … 0 − sin θ … 0 1 0 ⋮ ⋱ 0 0 0 1 … … sin θ 0 … 0 cos θ … 1 ⋱ ⋮ 0 1 ] i 行 U (\theta ; i, j) = \left[ \begin{array}{c c c c c c c c c} 1 & & & & & & & \\ & \ddots & & & 0 & & & \\ & & 1 & & & & & \\ & & \dots & \cos \theta & 0 & \dots & 0 & - \sin \theta & \dots \\ & & & 0 & 1 & & & \\ & & 0 & \vdots & & \ddots & & & 0 \\ & & & 0 & 0 & & 1 & & \\ & \dots & \dots & \sin \theta & 0 & \dots & 0 & \cos \theta & \dots \\ & & & & & & & 1 & \\ & & & & & & & \ddots \\ & \vdots & & & 0 & & & 1 \end{array} \right] \quad i \text {行} U ( θ ; i , j ) = 1 ⋱ … ⋮ 1 … 0 … cos θ 0 ⋮ 0 sin θ 0 0 1 0 0 0 … ⋱ … 0 1 0 − sin θ cos θ 1 ⋱ 1 … 0 … i 行 它相当于一个单位矩阵,只是它的 i i i i i i j j j j j j cos θ \cos \theta cos θ i i i j j j j j j i i i sin θ \sin \theta sin θ sin θ \sin \theta sin θ
练习 对于任一对指标 1 ⩽ i < j ⩽ n 1 \leqslant i < j \leqslant n 1 ⩽ i < j ⩽ n 0 ⩽ θ < 2 n 0 \leqslant \theta < 2n 0 ⩽ θ < 2 n U ( θ ; i , j ) U(\theta; i, j) U ( θ ; i , j ) M n ( R ) M_{n}(\mathbf{R}) M n ( R ) U ( θ ; i , j ) U(\theta; i, j) U ( θ ; i , j ) i , j i, j i , j θ \theta θ U ( θ ; i , j ) U(\theta; i, j) U ( θ ; i , j ) i i i j j j U ( θ ; i , j ) U(\theta; i, j) U ( θ ; i , j ) i i i j j j U ( θ ; i , j ) U(\theta; i, j) U ( θ ; i , j ) i , j i, j i , j i , j i, j i , j
2.2.4 例 Householder 变换。设 w ∈ C n w \in \mathbb{C}^n w ∈ C n U n ∈ M n U_n \in M_n U n ∈ M n U n = I − t w u ∗ U_n = I - t w u^* U n = I − tw u ∗ t = 2 ( w ∗ w ) t = 2(w^* w) t = 2 ( w ∗ w ) w w ∗ ∈ M m w w^* \in M_m w w ∗ ∈ M m w ∗ w w^* w w ∗ w w w w ( w ∗ w = 1 ) (w^* w = 1) ( w ∗ w = 1 ) t t t U n U_n U n I − 2 w w ∗ I - 2 w w^* I − 2 w w ∗ w w w U n U_n U n
练习 证明, U w U_{w} U w w w w w w w x ⊥ w x \perp w x ⊥ w U w x = x U_{w}x = x U w x = x U w W = − W U_{w}W = -W U w W = − W
练习 证明, U w U_{w} U w ( U w = U u ) (U_{w} = U_{u}) ( U w = U u ) U u U_{u} U u U w U_{w} U w
非常有效而精确的简化.
定理(2.2.2)给出了两个已知矩阵酉等价的一个必要而不充分的条件。我们能在此基础上再添加更多的恒等式,这些恒等式共同给出两个已知矩阵酉等价的必要充分条件。其中,下述简单概念起着关键的作用。设 s , t s, t s , t s , t s, t s , t
W ( s , t ) = s m 1 t n 1 ⋅ s m 2 t n 2 … s m k t n k , m 1 , n 1 , … , m k , n k ⩾ 0 (2.2.5) W (s, t) = s ^ {m _ {1}} t ^ {n _ {1}} \cdot s ^ {m _ {2}} t ^ {n _ {2}} \dots s ^ {m _ {k}} t ^ {n _ {k}}, \quad m _ {1}, n _ {1}, \dots , m _ {k}, n _ {k} \geqslant 0 \tag {2.2.5} W ( s , t ) = s m 1 t n 1 ⋅ s m 2 t n 2 … s m k t n k , m 1 , n 1 , … , m k , n k ⩾ 0 ( 2.2.5 ) 为关于 s s s t t t W ( s , t ) W(s, t) W ( s , t ) m 1 + n 1 + m 2 + n 2 + ⋯ + m k + n k m_{1} + n_{1} + m_{2} + n_{2} + \cdots + m_{k} + n_{k} m 1 + n 1 + m 2 + n 2 + ⋯ + m k + n k A ∈ M n A \in M_{n} A ∈ M n A A A A ∗ A^{*} A ∗
W ( A , A ∗ ) = A m 1 ( A ∗ ) n 1 A m 2 ( A ∗ ) n 2 … A m s ( A ∗ ) n s . W (A, A ^ {*}) = A ^ {m _ {1}} \left(A ^ {*}\right) ^ {n _ {1}} A ^ {m _ {2}} \left(A ^ {*}\right) ^ {n _ {2}} \dots A ^ {m _ {s}} \left(A ^ {*}\right) ^ {n _ {s}}. W ( A , A ∗ ) = A m 1 ( A ∗ ) n 1 A m 2 ( A ∗ ) n 2 … A m s ( A ∗ ) n s . 由于 A A A A ′ A^{\prime} A ′ W ( A , A ′ ) W(A, A^{\prime}) W ( A , A ′ )
如果 A A A B ∈ M n B \in M_{n} B ∈ M n U ∈ M n U \in M_{n} U ∈ M n A − U B U ′ A - UBU' A − U B U ′
W ( A , A ∗ ) = ( U B U ∗ ) m 1 ( U B ∗ U ∗ ) n … ( U B U ∗ ) m 1 ( U B ∗ U ∗ ) n = U B m [ I ∗ U ( B ∗ ) n 1 U ∗ … [ I B m ] U ∗ [ I ( B ∗ ) n 1 U ∗ − U B m 1 ( B ∗ ) n 1 … B m k ( B ∗ ) n k U ∗ = U W ( B , B ∗ ) U ′ . \begin{array}{l} W (A, A ^ {*}) = (U B U ^ {*}) ^ {m _ {1}} (U B ^ {*} U ^ {*}) ^ {n} \dots (U B U ^ {*}) ^ {m _ {1}} (U B ^ {*} U ^ {*}) ^ {n} \\ = U B ^ {m} \left[ I ^ {*} U (B ^ {*}) ^ {n _ {1}} U ^ {*} \dots [ I B ^ {m} ] U ^ {*} [ I (B ^ {*}) ^ {n _ {1}} U ^ {*} \right. \\ - U B ^ {m _ {1}} \left(B ^ {*}\right) ^ {n _ {1}} \dots B ^ {m _ {k}} \left(B ^ {*}\right) ^ {n _ {k}} U ^ {*} \\ = U W (B, B ^ {*}) U ^ {\prime}. \\ \end{array} W ( A , A ∗ ) = ( U B U ∗ ) m 1 ( U B ∗ U ∗ ) n … ( U B U ∗ ) m 1 ( U B ∗ U ∗ ) n = U B m [ I ∗ U ( B ∗ ) n 1 U ∗ … [ I B m ] U ∗ [ I ( B ∗ ) n 1 U ∗ − U B m 1 ( B ∗ ) n 1 … B m k ( B ∗ ) n k U ∗ = U W ( B , B ∗ ) U ′ . 因而, tr W ( A , A ∗ ) → tr U W ( B , B ∗ ) U ∗ = tr W ( B , B ∗ ) \operatorname{tr} W(A, A^*) \rightarrow \operatorname{tr} UW(B, B^*)U^* = \operatorname{tr} W(B, B^*) tr W ( A , A ∗ ) → tr U W ( B , B ∗ ) U ∗ = tr W ( B , B ∗ ) W ( s , t ) = t s W(s, t) = ts W ( s , t ) = t s
对所有可能的字 W ( s , t ) W(s, t) W ( s , t ) W ⋅ Spec c h W \cdot \operatorname{Spec} \mathbf{ch} W ⋅ Spec ch
2.2.6 定理 两个已知矩阵 A , B ∈ M n A, B \in M_{n} A , B ∈ M n
tr W ( A , A ′ ) = tr W ( B , B ′ ) (2.2.7) \operatorname {t r} W (A, A ^ {\prime}) = \operatorname {t r} W (B, B ^ {\prime}) \tag {2.2.7} tr W ( A , A ′ ) = tr W ( B , B ′ ) ( 2.2.7 ) 对于两个非交换元的每个字 W ( s , t ) W(s, t) W ( s , t )
Specht定理只能用来证明两个已知矩阵不酉等价。然而,除非在一些特殊情形(见习题6),它在证明两个已知矩阵是酉等价时可能失效,因为必须验证无限多个条件。幸运的是,有一个定理对Specht定理作了改进,它属于C. Pearcy。这个定理说明,只要对有限多个字验证迹恒等式(2.2.7)就够了。
2.2.8 定理 两个已知矩阵 A , B ∈ M n A, B \in M_{n} A , B ∈ M n tr W ( A , A ∗ ) = tr W ( B , B ∗ ) \operatorname{tr} W(A, A^{*}) = \operatorname{tr} W(B, B^{*}) tr W ( A , A ∗ ) = tr W ( B , B ∗ ) 2 n 2 2n^{2} 2 n 2 W ( s , t ) W(s, t) W ( s , t )
Pearcy定理中的有限限制是对Specht定理的一大改进,但是,如我们所知,这还是非常保守的。当 n = 2 n = 2 n = 2 W ( s , t ) = s W(s,t) = s W ( s , t ) = s s 2 s^2 s 2 t s ts t s 2 ( 2 ) 2 = 8 2(2)^2 = 8 2 ( 2 ) 2 = 8 n = 3 n = 3 n = 3 W ( s , t ) = s W(s,t) = s W ( s , t ) = s s 2 s^2 s 2 t s ts t s s 4 s^4 s 4 t s 2 ts^2 t s 2 t 2 s 2 t^2 s^2 t 2 s 2 t s t s tsts t s t s t s 2 t s ts^2 ts t s 2 t s t s 2 t 2 s ts^2 t^2 s t s 2 t 2 s 2 ( 3 ) 2 = 18 2(3)^2 = 18 2 ( 3 ) 2 = 18
习题 设 A = ∣ a i j ∣ ∈ M n ( R ) A = \left|a_{ij}\right| \in M_n(\mathbf{R}) A = ∣ a ij ∣ ∈ M n ( R ) ( A i = A ) (A^i = A) ( A i = A ) i ≠ j i \neq j i = j ∣ a i j ∣ \left|a_{ij}\right| ∣ a ij ∣ ( a i i − a j j ) 2 a i j − cot ( 2 θ ) (a_{ii} - a_{jj})^2 a_{ij} - \cot(2\theta) ( a ii − a jj ) 2 a ij − cot ( 2 θ ) θ \theta θ U ( θ ; i , j ) U(\theta; i, j) U ( θ ; i , j ) B − U ( θ ; i , j ) ∗ A U ( θ ; i , j ) = ( b i j ) B - U(\theta; i, j)^* AU(\theta; i, j) = (b_{ij}) B − U ( θ ; i , j ) ∗ A U ( θ ; i , j ) = ( b ij ) ∑ i ≤ j ∣ b i j ∣ 2 < ∑ i ≤ j ∣ a i j ∣ 2 \sum_{i \leq j} |b_{ij}|^2 < \sum_{i \leq j} |a_{ij}|^2 ∑ i ≤ j ∣ b ij ∣ 2 < ∑ i ≤ j ∣ a ij ∣ 2 B B B A A A
关于实对称矩阵(或一般的实矩阵)特征值的Givens法也是利用平面旋转,但采用的方式有所不同。证明,一个对称矩阵 A = [ a i j ] ∈ M n ( R ) A = [a_{ij}] \in M_n(\mathbb{R}) A = [ a ij ] ∈ M n ( R ) A ∈ M n ( R ) A \in M_n(\mathbb{R}) A ∈ M n ( R ) U 1 , 3 U_{1,3} U 1 , 3 U 1 , 3 A U 1 , 3 U_{1,3}AU_{1,3} U 1 , 3 A U 1 , 3 n n n
证明,每个矩阵 A ∈ M n A \in M_n A ∈ M n A ∈ M 2 A \in M_2 A ∈ M 2 A − ( 1 / 2 ) ( tr A ) I A - (1/2)(\operatorname{tr} A)I A − ( 1/2 ) ( tr A ) I tr A = 0 \operatorname{tr} A = 0 tr A = 0 x ∈ C 2 x \in \mathbb{C}^2 x ∈ C 2 x ∗ A x = 0 x^* A x = 0 x ∗ A x = 0 U − [ x , y ] ∈ M 2 U - [x, y] \in M_2 U − [ x , y ] ∈ M 2 U ∗ A U U^* A U U ∗ A U x x x w , z w, z w , z A A A ± λ \pm \lambda ± λ λ = 0 \lambda = 0 λ = 0 x = w x = w x = w λ ≠ 0 \lambda \neq 0 λ = 0 x ( θ ) = e i θ w + z x(\theta) = e^{i\theta} w + z x ( θ ) = e i θ w + z θ ∈ R \theta \in \mathbb{R} θ ∈ R x ( θ ) ≠ 0 x(\theta) \neq 0 x ( θ ) = 0 θ ∈ R \theta \in \mathbb{R} θ ∈ R x ( θ ) ∗ A x ( θ ) = 0 x(\theta)^* A x(\theta) = 0 x ( θ ) ∗ A x ( θ ) = 0 θ \theta θ x − x ( θ ) / [ x ( θ ) ′ x ( θ ) ] 1 2 x - x(\theta) / [x(\theta)' x(\theta)]^{\frac{1}{2}} x − x ( θ ) / [ x ( θ ) ′ x ( θ ) ] 2 1 A ∈ M 2 ( R ) A \in M_2(\mathbb{R}) A ∈ M 2 ( R ) U = U ( θ ; 1 , 2 ) U = U(\theta; 1, 2) U = U ( θ ; 1 , 2 ) U T A U U^T A U U T A U f ( A ) = max { ∣ a n − a j n ∣ : i , j = 1 , 2 , … , n } f(A) = \max \{|a_n - a_{jn}| : i, j = 1, 2, \dots, n\} f ( A ) = max { ∣ a n − a jn ∣ : i , j = 1 , 2 , … , n } A 2 = [ a n a n a n a n ] A_2 = \begin{bmatrix} a_n & a_n \\ a_n & a_n \end{bmatrix} A 2 = [ a n a n a n a n ] i , j i, j i , j f ( A ) = ∣ a n − a j n ∣ f(A) = |a_n - a_{jn}| f ( A ) = ∣ a n − a jn ∣ U 2 ∈ M 2 U_2 \in M_2 U 2 ∈ M 2 U 2 ∗ A 2 U 2 U_2^* A_2 U_2 U 2 ∗ A 2 U 2 2 × 2 2 \times 2 2 × 2 U ( θ ; i , j ) U(\theta; i, j) U ( θ ; i , j ) U 2 U_2 U 2 U ( i , j ) ∈ M n U(i, j) \in M_n U ( i , j ) ∈ M n f ( U ( i , j ) ∗ A U ( i , j ) ) < f ( A ) f(U(i, j)^* A U(i, j)) < f(A) f ( U ( i , j ) ∗ A U ( i , j )) < f ( A ) f ( A ) ≠ 0 f(A) \neq 0 f ( A ) = 0 U ∈ M n U \in M_n U ∈ M n f ( U ∗ A U ) < f ( A ) f(U^* A U) < f(A) f ( U ∗ A U ) < f ( A ) R ( A ) = { U ∗ A U ; U ∈ M n R(A) = \{U^* A U; U \in M_n R ( A ) = { U ∗ A U ; U ∈ M n R ( A ) R(A) R ( A ) f f f R ( A ) R(A) R ( A ) C ∈ R ( A ) C \in R(A) C ∈ R ( A ) f ( C ) = min { f ( B ) ; B ∈ R ( A ) } f(C) = \min \{f(B); B \in R(A)\} f ( C ) = min { f ( B ) ; B ∈ R ( A )} f ( C ) f(C) f ( C ) f ( C ) = 0 f(C) = 0 f ( C ) = 0
证明,用Householder变换可以把一个具有Euclid长度 r = ( x ′ x ) 1 / 2 r = (x^{\prime}x)^{1/2} r = ( x ′ x ) 1/2 x ∈ R x \in \mathbb{R} x ∈ R r r r y ∈ R n y \in \mathbb{R}^{n} y ∈ R n y ≠ x y \neq x y = x U w U_{w} U w w = x − y w = x - y w = x − y x , y ∈ C n x, y \in \mathbb{C}^{n} x , y ∈ C n
76
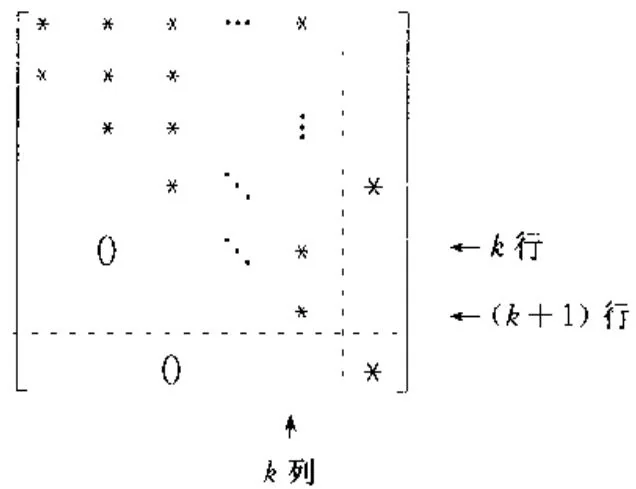
计算 A ∈ M n ( R ) A \in M_{n}(\mathbf{R}) A ∈ M n ( R ) A A A j j j ( j + 1 ) (j + 1) ( j + 1 ) 0 ( j = 1 , ⋯ , k ) 0 (j = 1, \cdots, k) 0 ( j = 1 , ⋯ , k )
的矩阵,经一个用Householder变换所确定的实正交相似可以变成一个同形的矩阵。由此得出,任一个矩阵 A ∈ M n ( R ) A \in M_{n}(\mathbf{R}) A ∈ M n ( R ) ( n − 2 (n - 2 ( n − 2 A ∈ M n ( R ) A \in M_{n}(\mathbf{R}) A ∈ M n ( R ) ( k + 1 ) (k + 1) ( k + 1 ) U ∈ M n U \in M_{n} U ∈ M n ( n − k ) (n - k) ( n − k ) [ 1 , 0 , … , 0 ] T ∈ R n [1,0,\dots ,0]^T \in \mathbb{R}^n [ 1 , 0 , … , 0 ] T ∈ R n
[ I 0 0 U ] ∈ M n \left[ \begin{array}{c c} I & 0 \\ 0 & U \end{array} \right] \in M _ {n} [ I 0 0 U ] ∈ M n 确定的相似可变换整个矩阵,并且看到所想要的0子块出现了。
设 A ∈ M n A \in M_{n} A ∈ M n B , C ∈ M n B, C \in M_{n} B , C ∈ M n B B B C C C
(a) [ A 0 0 B ] \left[ \begin{array}{ll}A & 0\\ 0 & B \end{array} \right] [ A 0 0 B ] [ A 0 0 C ] \left[ \begin{array}{ll}A & 0\\ 0 & C \end{array} \right] [ A 0 0 C ]
(b) [ B 0 B ⋱ 0 B ] \left[ \begin{array}{cccc}B & & & 0\\ & B & & \\ & & \ddots & \\ 0 & & & B \end{array} \right] B 0 B ⋱ 0 B [ C 0 C ⋱ 0 C ] \left[ \begin{array}{cccc}C & & & 0\\ & C & & \\ & & \ddots & \\ 0 & & & C \end{array} \right] C 0 C ⋱ 0 C
(A) [ A 0 B ⋱ 0 B ] \left[ \begin{array}{cccc}A & & & 0\\ & B & & \\ & & \ddots & \\ 0 & & & B \end{array} \right] A 0 B ⋱ 0 B [ A 0 C ⋱ 0 C ] \left[ \begin{array}{cccc}A & & & 0\\ & C & & \\ & & \ddots & \\ 0 & & & C \end{array} \right] A 0 C ⋱ 0 C
证明:诸某个次数 k k k 2 k − 1 2^{k-1} 2 k − 1 W ( s , t ) \mathbf{W}(s, t) W ( s , t ) 4 n 2 4n^{2} 4 n 2 2 n 2 2n^{2} 2 n 2
试给出两个 2 × 2 2 \times 2 2 × 2
进一步阅读与注释 关于定理(2.2.6)的原始证明可参看W. Specht, “Zur Theorie der Matrizen II,” Jahresbericht der Deutschen Mathematiker Vereinigung 50(1940), 19-23. 定理 (2.2.8) 的证明可见 C. Pearcy, “A Complete Set of Unitary Invariants for Operators Generating Finite W ∗ W^{*} W ∗ 3 × 3 3 \times 3 3 × 3