59.1 RNN层的实现

首先使用式子来介绍RNN。我们以输入为时间序列数据 $x_{t}$ 、输出为隐藏状态 $h_{t}$ 的RNN为例进行思考。这里的 $t$ 指的是时间序列数据的时间 $t$ （或

第 $t$ 个)。另外，由于RNN的状态被称为隐藏状态(hidden state)，所以在式子中用 $\pmb{h}$ 来表示RNN的状态。下面是RNN的正向传播的式子。

先来看一下式子59.1中的符号。RNN有两个权重：一个是权重 $\mathbf{W}_{\mathbf{x}}$ ，用于将输入 $\mathbf{x}$ 转换为隐藏状态 $\mathbf{h}$ ；另一个是权重 $\mathbf{W}_{h}$ ，用于将前一个时刻的RNN的输出转换为下一个时刻的输出。另外还有偏置 $\mathbf{b}$ 。这里的 $h_{t-1}$ 和 $\mathbf{x}_t$ 是行向量。

式子59.1中首先进行矩阵乘积的计算，然后使用tanh函数（双曲正切函数）对它们的和进行转换。其结果是时刻 $t$ 的输出 $h_t$ 。这个 $h_t$ 既用在其他层，也用在下一个时刻的RNN层(自身）。

下面来实现DeZero的RNN层。按照之前的方法进行操作，RNN层继承于Layer类，它的forward方法中是正向传播的处理。下面是RNN层的代码（将此代码添加到dezero/layers.py中）。

dezero/layers.py

class RNN(Layer): def __init__(self, hidden_size, in_size=None): super().__init_(self.x2h = Linear(hidden_size, in_size=in_size) self.h2h = Linear(hidden_size, in_size=in_size, nobias=True) self.h = None def reset_state(self): self.h = None def forward(self, x): if self.h is None: h_new = F.tanh(self.x2h(x)) else: h_new = F.tanh(self.x2h(x) + self.h2h(self.h)) self.h = h_new return h_new

首先，初始化方法__init__接收hidden_size和in_size。如果in_size为None，则意味着只指定了隐藏层的大小。在这种情况下，输入大小会自动从正向传播时传来的数据中获得。__init__方法创建以下两个线性层。

• x2h：将输入x转换为隐藏状态h的全连接层

• h2h：将上一个隐藏状态转换为下一个隐藏状态的全连接层

之后forward方法的实现中根据self.h(隐藏状态)是否存在来切换处理。第1次self.h == None，所以只能从输入x计算隐藏状态。从第2次之后，forward方法使用以前的隐藏状态(self.h)计算新的隐藏状态。另外，RNN层中准备了一个叫reset_state的方法，这是用于重置隐藏状态的方法。

如式子59.1所示，RNN的偏置只有一个。因此，我们只使用x2h的偏置，省略h2h(Linear层)的偏置(上面的代码将h2h初始化为nobias=True)。

现在向上面的RNN层传入实际的数据。尝试运行下面的代码。

import numpy as np  
importdezero.layersasL  
rnn  $=$  L.RNN(10） #只指定隐藏层的大小  
x  $\equiv$  np.random.randint(1，1)  
h  $\equiv$  rnn(x)  
print(h.shape)

运行结果

(1, 10)

上面的代码创建的是虚拟的数据，即形状为(1，1)的x。这表示批量大小为1(即有一个数据)，数据的维度为1。将这个输入x传给rnn，可得隐藏状态h。此时的计算图如图59-2所示。

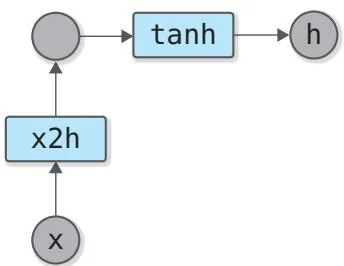
图59-2 第一次传x时的计算图（x2h是Linear层）

接下来继续传数据。假设紧接着前面的代码运行 $y = \text{rnn}(np.random.randint(1, 1))$ ，此时的计算图如图59-3所示。

图59-3 处理完第2个输入数据后的计算图

图59-3是在图59-2的计算图的基础上“成长”起来的计算图。正是RNN的隐藏状态使得这种“成长”成为可能。通过使用之前保存的隐藏状态，RNN的计算图与之前的计算图建立了连接。

如图59-3所示，RNN创建了包含所有输入数据的计算图。因此，RNN可以学习输入数据之间的“关系”。在图59-3中出现了2个x2h实例，但它们是同一个Linear实例，而且使用了相同的权重。