59.2 RNN模型的实现

下面使用RNN层来实现神经网络(模型)。这里要用到将RNN层的隐藏状态转换为输出的Linear层。代码如下所示，类名为SimpleRNN。

steps/step59.py

fromdezeroimportModel   
importdezero-functionsasF   
importdezero.layersasL   
classSimpleRNN(Model): def__init__(self,hidden_size,out_size): super(）.__init_() self.rnn  $=$  L.RNN(hidden_size) self.fc  $=$  L.Linear(out_size) defreset_state(self): self.rnn.reset_state() defforward(self,x): h  $=$  self.rnn(x) y  $=$  self.fc(h) returny

上面的代码向Linear层添加了实例变量fc。这个Linear层接收RNN层的隐藏状态并计算输出。另外，上面的模型使用reset_state方法重置RNN层的隐藏状态。现在试着用这个模型进行训练。这里使用均方误差(mean_squared_error函数)作为损失函数。求梯度的代码如下所示。

seq_data = [np.random.randint(1, 1) for _ in range(1000)] # 虚拟的时间序列数据  
xs = seq_data[0:-1]  
ts = seq_data[1:] # xs的下一个时间步的数据  
model = SimpleRNN(10, 1)  
loss, cnt = 0, 0  
for x, t in zip(xs, ts):  
    y = model(x)  
    loss += F.mean_squared_error(y, t)

cnt  $+ = 1$    
if cnt  $= = 2$  .. model.cleargrads() loss.backup(） break

首先创建虚拟的时间序列数据 seq_data。我们想训练的是基于该时间序列数据预测下一个时间步的数据的模型。为此需要保存训练数据，即输入数据的下一个时间步的数据。

然后是关键的反向传播，上面的代码只是一个示例，它在第2个输入数据到来时进行反向传播。传第2个输入数据时的计算图如图59-4所示。

创建了如图59-4所示的计算图后，我们就可以通过loss.backup()求出每个参数的梯度。这种在由一系列的输入数据组成的计算图上进行的反向传播叫作基于时间的反向传播(Backpropagation Through Time, BPTT)，它表示回溯时间进行反向传播。

RNN可以学到输入数据的排列方式的模式。数据排列的“顺序”对应于时间序列数据的“时间”。因此，Backpropagation Through Time中用到了Time(时间)一词。

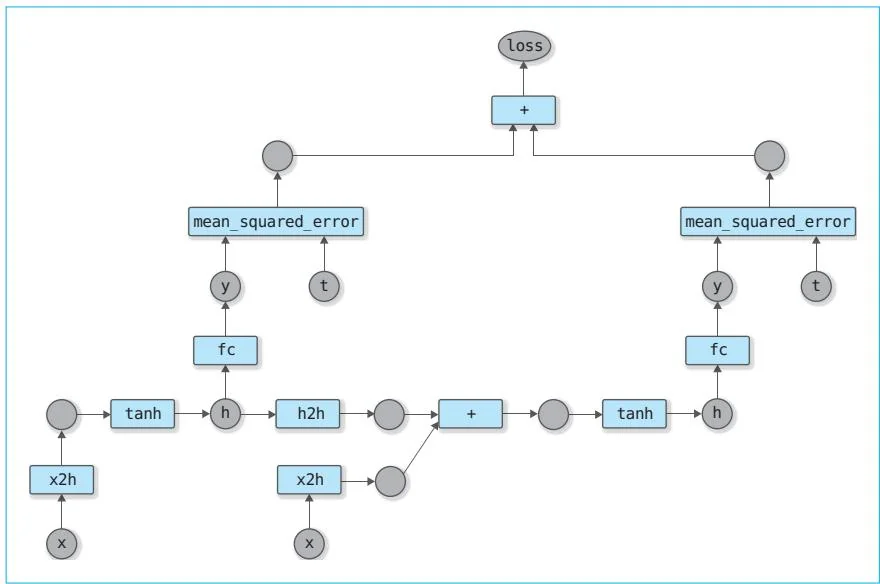
图59-4 应用损失函数后的计算图

图59-4是有两个输入数据时的计算图。当然，输入数据可以是10个、100个，甚至是任何数量。计算图将根据输入数据的数量变长。不过为了更好地执行反向传播，计算图到一定的长度后需要“截断”，这就是TruncatedBPTT（truncate的意思是“截断”或“切断”）。在上面的例子中，截断发生在两个输入数据处。

在进行Truncated BPTT时，需要注意保留RNN的隐藏状态。我们可以思考一下对图59-4的计算图进行反向传播后，传入下一个输入数据的情况。在此情况下，RNN的隐藏状态需要从前一个隐藏状态开始。具体如图59-5所示。

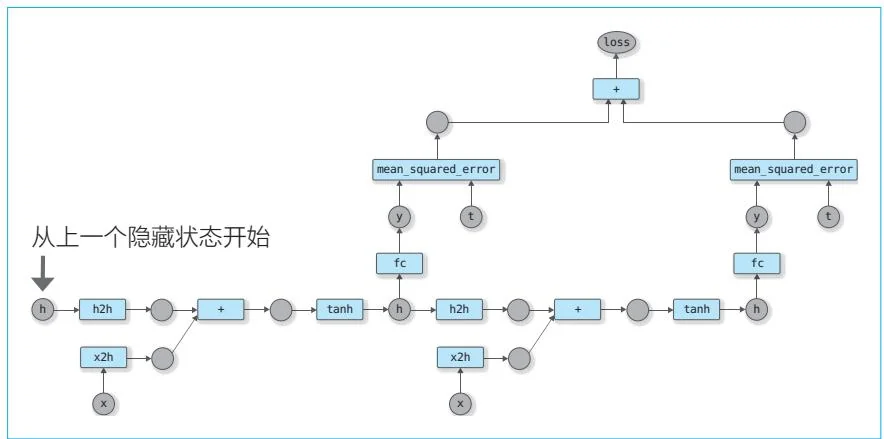
图59-5 在下一次迭代中创建的计算图

图59-5中的第一个隐藏状态从上一个隐藏状态开始。对于该隐藏状态的变量，我们需要切断计算上的连接。这样一来，梯度将不再向上一次训练的计算图传播（这就是“截断的BPTT”）。