5.2 反向传播的推导

下面仔细观察式子5.2。式子5.2表示复合函数的导数可以分解为各函数导数的乘积。但是，它并没有规定各导数相乘的顺序。当然，这一点我们可以自由决定。这里，我们按照式子5.3的方式以输出到输入的顺序进行计算①。

式子5.3按照从输出到输入的顺序进行导数的计算，计算方向与平时相反。这时，式子5.3的计算流程如图5-2所示。

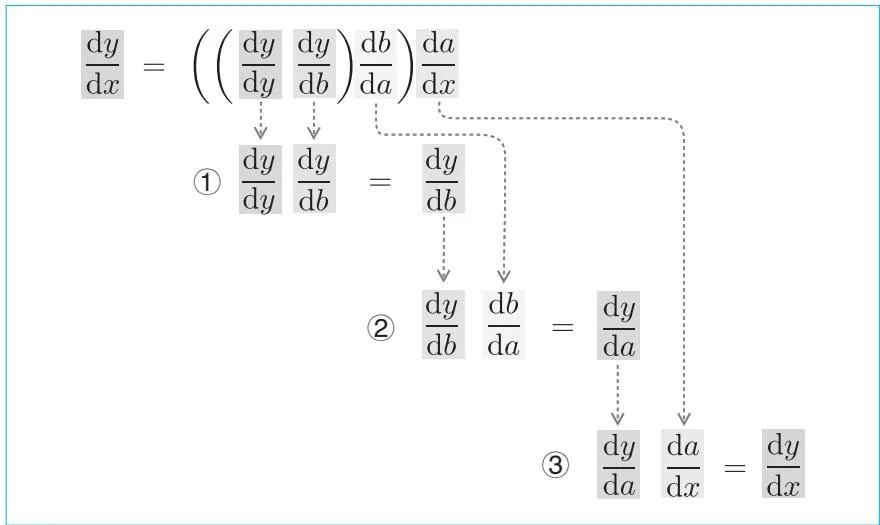
图5-2 从输出端的导数开始依次进行计算的流程（参见彩图）

在图5-2中，导数是按照从输出 $y$ 到输入 $x$ 的方向依次相乘计算得出的。通过这种方法，最终得到 $\frac{\mathrm{dy}}{\mathrm{dx}}$ 。图5-3是相应的计算图。

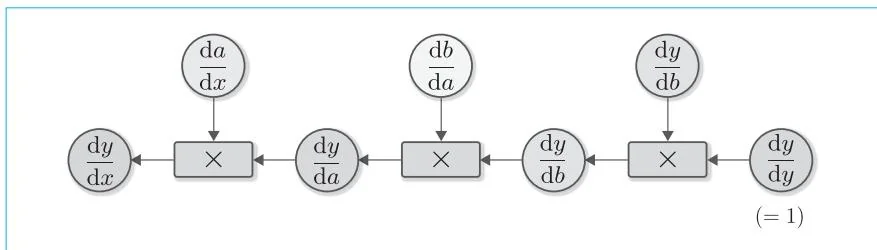
图5-3 求 $\frac{\mathrm{dy}}{\mathrm{dx}}$ 的计算图

下面仔细观察图5-3。我们先从 $\frac{\mathrm{dy}}{\mathrm{dy}} (= 1)$ 开始，计算它与 $\frac{\mathrm{dy}}{\mathrm{db}}$ 的乘积。这里的 $\frac{\mathrm{dy}}{\mathrm{db}}$ 是函数 $y = C(b)$ 的导数。因此，如果用 $C'$ 表示函数 $C$ 的导函数，我们就可以把式子写成 $\frac{\mathrm{dy}}{\mathrm{db}} = C'(b)$ 。同样，有 $\frac{\mathrm{db}}{\mathrm{da}} = B'(a)$ ， $\frac{da}{dx} = A'(x)$ 。基于以上内容，图5-3可以简化成图5-4。

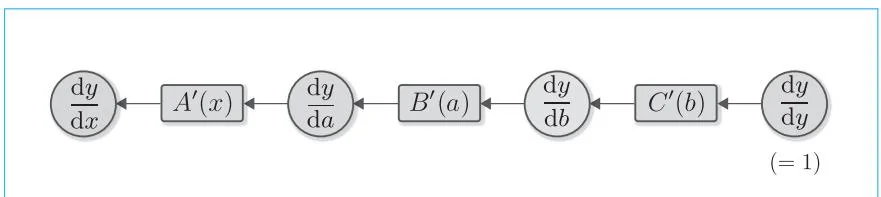
图5-4 简化后的反向传播计算图 $\left(A^{\prime}(x)\right)$ 的乘法在图中简化表示为节点 $A^{\prime}(x)$ )

图5-4中把导函数和乘号合并表示为一个函数节点。这样导数计算的流程就明确了。从图5-4中可以看出，“ $y$ 对各变量的导数”从右向左传播。这就是反向传播。这里重要的一点是传播的数据都是 $y$ 的导数。具体来说，就是 $\frac{\mathrm{dy}}{\mathrm{dy}}$ 、 $\frac{\mathrm{dy}}{\mathrm{db}}$ 、 $\frac{\mathrm{dy}}{\mathrm{da}}$ 和 $\frac{\mathrm{dy}}{\mathrm{dx}}$ 这种“ $y$ 对 $x$ 变量的导数”在传播。

像式子5.3那样将计算顺序规定为从输出到输入，是为了传播 $y$ 的导数。换言之，就是把 $y$ 当作“重要人物”。如果按照从输入到输出的顺序计算，输入 $x$ 就是“重要人物”。在这种情况下，传播的导数将是 $\frac{\mathrm{d}x}{\mathrm{d}x} \rightarrow \frac{\mathrm{d}a}{\mathrm{d}x} \rightarrow \frac{\mathrm{d}b}{\mathrm{d}x} \rightarrow \frac{\mathrm{d}y}{\mathrm{d}x}$ 这种形式，也就是对 $x$ 的导数进行传播。

许多机器学习问题采用了以大量参数作为输入，以损失函数作为最终输出的形式。损失函数的输出(在许多情况下)是一个标量值，它是“重要人物”。这意味着我们需要找到损失函数对每个参数的导数。在这种情况下，如果沿着从输出到输入的方向传播导数，只要传播一次，就能求出对所有参数的导数。因为该方法的计算效率较高，所以我们采用反向传播导数的方式。