5.3 用计算图表示

下面我们把正向传播的计算图(图5-1)和反向传播的计算图(图5-4)以上下排列的方式画出来。

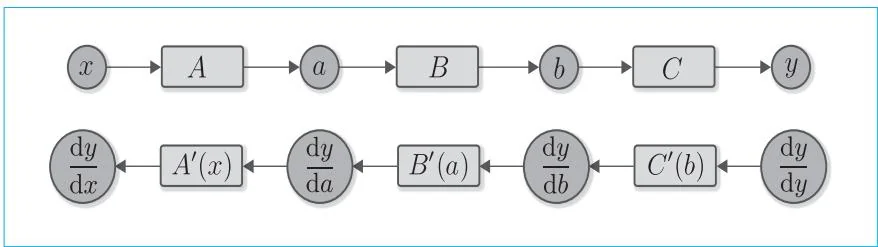
图5-5 正向传播和反向传播

从图5-5可以看出，正向传播和反向传播之间存在明确的对应关系。例如，正向传播时的变量 $a$ 对应于反向传播时的导数 $\frac{\mathrm{dy}}{\mathrm{da}}$ 。同样， $b$ 对应于 $\frac{\mathrm{dy}}{\mathrm{db}}$ ， $x$ 对应于 $\frac{\mathrm{dy}}{\mathrm{dx}}$ 。我们也可以看出函数之间存在对应关系。例如，函数 $B$ 的反向传播对应于 $B'(a)$ ， $A$ 对应于 $A'(x)$ 。这样一来，我们可以认为变量有普通值和导数值，函数有普通计算（正向传播）和求导计算（反向传播）。于是，反向传播就设计好了。

最后来关注一下图5-5中 $C^\prime (b)$ 的函数节点。它是 $y = C(b)$ 的导数，但要注意的是，计算 $C^\prime (b)$ 需要用到 $b$ 的值。同理，要计算 $B^{\prime}(a)$ 就得输入 $a$ 的值。这意味着进行反向传播时需要用到正向传播中使用的数据。因此，在实现反向传播时，需要先进行正向传播，并且存储各函数输入的变量值，也就是前面例子中的 $x$ 、 $a$ 和 $b$ ，之后就能对每个函数进行反向传播的计算了。

以上就是反向传播理论知识的相关内容，这是本书的难点之一。大家现在可能还没完全弄明白，但是实际运行代码后，就会理解得越来越透彻。在下一个步骤，我们将实现反向传播，并通过实际运行代码来验证它。

步骤6

手动进行反向传播

上一个步骤介绍了反向传播的机制。本步骤将扩展现有的Variable类和Function类，实现通过反向传播来求导的功能。首先是Variable类。