0x22 深度优先搜索

深度优先搜索（DFS，DepthFirstSearch），顾名思义，就是按照深度优先的顺序对“问题状态空间”进行搜索的算法。在第0x00章中，我们多次把一个问题的求解看作对问题状态空间的遍历与映射。从本章起，我们可以进一步把“问题空间”类比为一张图，其中的状态类比为节点，状态之间的联系与可达性就用图中的边来表示，那么使用深度优先搜索算法求解问题，就相当于在一张图上进行深度优先遍历。

读者可能发现，深度优先搜索与“递归”和“栈”密切相关。我们倾向于认为“递归”是与递推相对的一种单纯的遍历方法，除了搜索之外，还有许多算法都可以用递归实现。而“深搜”是一类包括遍历形式、状态记录与检索、剪枝优化等算法整体设计的统称。

在研究深度优先搜索算法之前，我们先来定义该过程产生的“搜索树”结构。在对图进行深度优先遍历处于点 $x$ 时，对于某些边 $(x, y)$ ， $y$ 是一个尚未访问过的节点，程序从 $x$ 成功进入了更深层的对 $y$ 的递归；对于另外的一些边 $(x, y)$ ， $y$ 已经被访问过，从而程序继续考虑其他分支。我们称所有点（问题空间中的状态）与成功发生递归的边（访问两个状态之间的移动）构成的树为一棵“搜索树”。整个深搜算法就是基于该搜索树完成的一一为了避免重复访问，我们对状态进行记录和检索；为了使程序更加高效，我们提前剪除搜索树上不可能是答案的子树和分支，不去进行遍历。

我们在0x03节中使用递归实现的指数型、排列型和组合型枚举，其实就是深搜的三种最简单的形式。与之相关的子集和问题、全排列问题、N皇后问题等都是可以用深搜求解的经典NPC问题。许多程序设计的入门书籍均以这几个问题作为例子讲解深搜算法，故本书就不再赘述，请读者确保自己已经掌握并能够实现这几个经典问题的深搜解法。在本节中，我们先通过几道更加综合性的例题直观地感受一下深度优先搜索算法。下节我们将进一步系统地讨论各类剪枝技巧。

【例题】小猫爬山 CODEVS4228

Freda 和 Rainbow 运送 $N$ 只小猫坐索道下山。索道上的缆车最大承重量为 $W$ ，而 $N$ 只小猫的重量分别是 $C_{1}, C_{2}, \cdots, C_{N}$ 。当然，每辆缆车上的小猫的重量之和不能超过 $W$ 。每租用一辆缆车，Freda 和 Rainbow 就要付 1 美元，所以他们想知道，最少需要付多少美元才能把这 $N$ 只小猫都运送下山？ $1 \leq N \leq 18, 1 \leq C_{i} \leq W \leq 10^{8}$ 。

可以使用深度优先搜索算法解决本题。在搜索的过程中，我们可以尝试依次把每一

只小猫分配到一辆已经租用的缆车上，或者新租一辆缆车安置这只小猫。于是，我们实时关心的状态有：已经运送的小猫有多少只，已经租用的缆车有多少辆，每辆缆车上当前搭载的小猫重量之和。

编写函数 dfs(now, cnt) 处理第 now 只小猫的分配过程（前 now-1 只已经装载），并且目前已经租用了 cnt 辆缆车。对于已经租用的这 cnt 辆缆车的当前搭载量，我们使用一个全局数组 cab[] 来记录。

now, cnt和cab数组共同标识着问题状态空间所类比的“图”中的一个“节点”。在这个“节点”上，我们至多有 $cnt + 1$ 个可能的分支：

尝试把第 now 只小猫分配到已经租用的第 $i(1 \leq i \leq cnt)$ 辆缆车上。如果第 $i$ 辆缆车还装得下，我们就在 cab[i] 中累加 $C_{now}$ ，然后递归 dfs(now + 1, cnt)。
尝试新租一辆缆车来安置这只小猫，也就是令 $cab[cnt + 1] = C_{now}$ ，然后递归 $\mathrm{dfs}(now + 1, cnt + 1)$ 。

当 $now = N + 1$ 时，说明搜索到了递归边界，此时就可以用 cnt 更新答案。

为了让搜索过程更加高效，我们可以加入一个很显然的优化：如果在搜索的任何时刻发现cnt已经大于或等于已经搜到的答案，那么当前分支就可以立即回溯了。另外，重量较大的小猫显然比重量较轻的小猫更“难”运送，我们还可以在整个搜索前把小猫按照重量递减排序，优先搜索重量较大的小猫，减少搜索树“分支”的数量。读者可以比较加入这两条优化前后，程序运行时间的差异。

int c[20], cab[20], n, w, ans;  
void dfs(int now, int cnt) {  
    if (cnt >= ans) return;  
    if (now == n + 1) {  
        ans = min(ans, cnt);  
        return;  
    }  
    for (int i = 1; i <= cnt; i++) { // 分配到已租用缆车  
        if (cab[i] + c(now) <= w) { // 能装下  
            cab[i] += c(now);  
            dfs(now + 1, cnt);  
            cab[i] -= c(now); // 还原现场  
        }  
    }  
    cabCNT + 1 = c(now);  
    dfs(now + 1, cnt + 1);  
    cabCNT + 1 = 0;

}  
int main() {  
    cin >> n >> w;  
    for (int i = 1; i <= n; i++) cin >> c[i];  
    sort(c + 1, c + n + 1); reverse(c + 1, c + n + 1);  
    ans = n; // 最多用 n 辆缆车，每只猫一辆  
    dfs(1, 0); // 搜索入口  
    cout << ans << endl;  
}

【例题】Sudoku FOJ2676/3074

数独是一种传统益智游戏，你需要把一个 $9*9$ 的数独（如右图）补充完整，使得图中每行、每列、每个 $3*3$ 的九宫格内数字 $1\sim 9$ 均恰好出现一次。请编写一个程序填写数独。POJ3074的测试数据难度要高于POJ2676。

数独问题的搜索框架非常简单，我们关心的“状态”就是数独的每个位置上填了什么数。在每个状态下，我们找出一个还没有填的位置，检查有哪些合法的数字可以填。这些合法的数字就构成该状态向下继续递归的“分支”。

搜索边界分为两种：一是如果所有位置都被填满，就找到了一个解；二是如果发现某个位置没有能填的合法数字，说明当前分支搜索失败，应该回溯去尝试其他分支。

如下图所示，就是用深度优先搜索算法求解Sudoku问题产生的一棵搜索树。

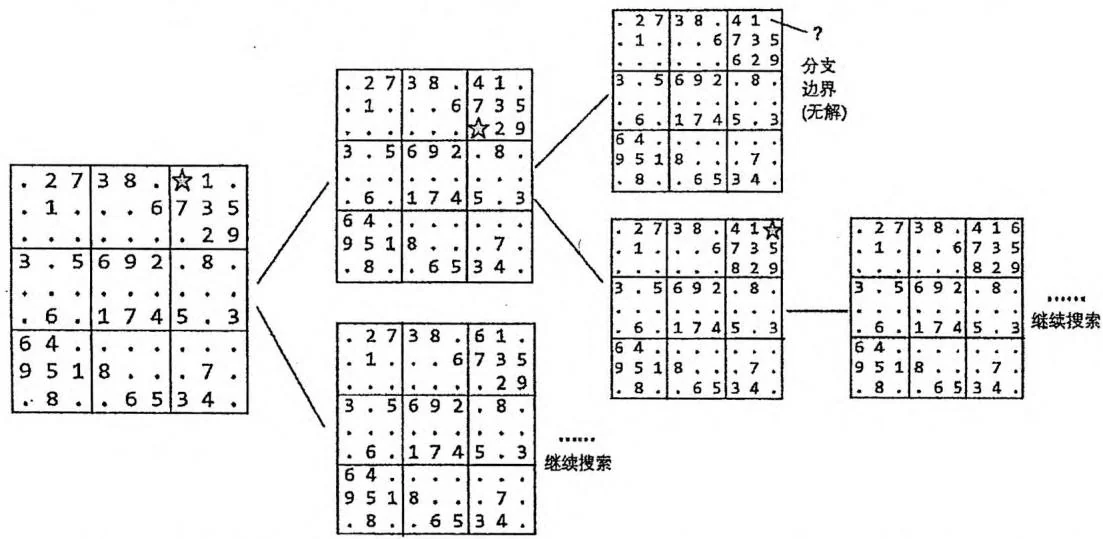
提醒：在任意一个状态下，我们只需要找出1个位置，考虑该位置上填什么数（如

上页图搜索树的根节点只有2个分支)，不需要枚举所有的位置和可填的数字向下递归（因为其他位置在更深的层次会被搜索到）。新手常犯的错误就是重叠、混淆“层次”和“分支”，造成重复遍历若干棵覆盖同一状态空间的搜索树，致使搜索的复杂度大规模增长。

然而，数独问题的“搜索树”规模仍然很大，直接盲目搜索的效率实在不能接受。试想，如果是人类来玩数独，策略一定是先填上“已经能够唯一确定的位置”，然后从那些填得比较满、选项比较少的位置实施突破。所以在搜索算法中，也应该采取类似的策略：在每个状态下，从所有未填的位置里选择“能填的合法数字”最少的位置，考虑该位置上填什么数，作为搜索的分支，而不是任意找出1个位置。

在搜索程序中，影响时间效率的因素除了搜索树的规模（影响算法的时间复杂度），还有在每个状态上记录、检索、更新的开销（影响程序运行的“常数”时间）。我们可以使用位运算来代替数组执行“对数独各个位置所填数字的记录”以及“可填性的检查与统计”。这就是我们所说的程序“常数优化”。具体地说：

对于每行、每列、每个九宫格，分别用一个9位二进制数（全局整数变量）保存哪些数字还可以填。
对于每个位置，把它所在行、列、九宫格的3个二进制数做位与(&)运算，就可以得到该位置能填哪些数，用lowbit运算就可以把能填的数字取出。
当一个位置填上某个数后，把该位置所在的行、列、九宫格记录的二进制数的对应位改为0，即可更新当前状态；回溯时改回1即可还原现场。

上述算法已经能够快速求解 $9*9$ 的数独问题，并且程序的实现十分简洁。书后的光盘中给出了一份参考程序。

通过本节的内容，读者可能已经发现，使用搜索解决问题的框架思想并不难，但如何减小搜索树的规模、如何快速遍历搜索树却是一门高深的学问。在接下来的两节中，我们就来重点研究这门学问。我们还会探究16*16的数独问题，进一步优化数独搜索算法。

0x22_深度优先搜索

0x22 深度优先搜索

【例题】小猫爬山 CODEVS4228