0x24_迭代加深
0x24迭代加深
迭代加深
深度优先搜索每次选定一个分支,不断深入,直至到达递归边界才回溯。这种策略带有一定的缺陷。试想以下情况:搜索树每个节点的分支数目非常多,并且问题的答案在某个较浅的节点上。如果深搜在一开始选错了分支,就很可能在不包含答案的深层子树上浪费许多时间。
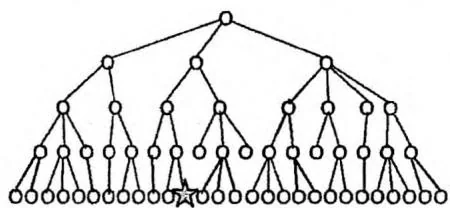
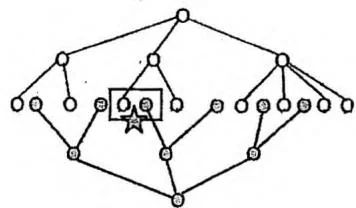
如果下图左半部分是问题的状态空间,五角星标识着答案,那么深度优先搜索算法产生的搜索树就如下图右半部分所示,算法在矩形圈出的深层子树上浪费了很多时间。
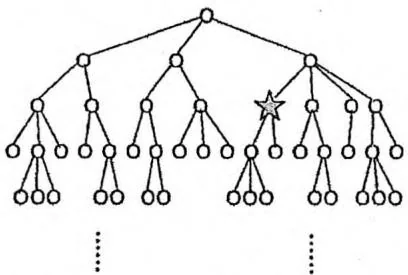
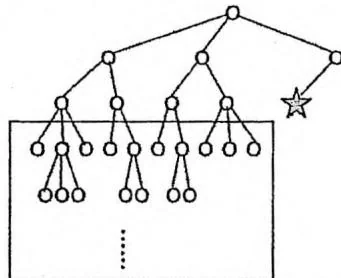
此时,我们可以从小到大限制搜索的深度,如果在当前深度限制下搜不到答案,就把深度限制增加,重新进行一次搜索,这就是迭代加深思想。所谓“迭代”,就是以上一次的结果为基础,重复执行以逼近答案的意思。迭代加深DFS的过程如下:
0
限制搜索深度为1 搜索失败
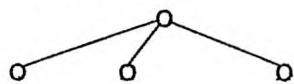
限制搜索深度为2 搜索失败
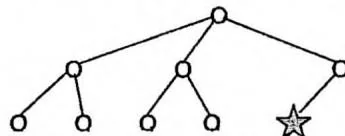
限制搜索深度为3 找到答案
虽然该过程在深度限制为 时,会重复搜索第 层的节点,但是当搜索树节点分支数目较多时,随着层数的深入,每层节点数会呈指数级增长,这点重复搜索与深层子树的规模相比,实在是小巫见大巫了。
总而言之,当搜索树规模随着层次的深入增长很快,并且我们能够确保答案在一个较浅层的节点时,就可以采用迭代加深的深度优先搜索算法来解决问题。读者可以进行大致的估算,有些题目描述甚至会包含“如果10步以内搜不到结果就算无解”的字样。
【例题】Addition Chains POJ2248
满足如下条件的序列 被称为“加成序列”:
对于每个 都存在两个整数 和 ( , 和 可以相等),使得 。
你的任务是:给定一个整数 ,找出符合上述条件的长度 最小的“加成序列”。如果有多个满足要求的答案,只需要找出任意一个可行解。 。
搜索框架:依次搜索序列中的每个位置 ,枚举 和 作为分支,把 和 的和填到 上,然后递归填写下一个位置。
加入以下剪枝:
1.优化搜索顺序
为了让序列中的数尽快逼近 ,在枚举 和 时从大到小枚举。
排除等效冗余
对于不同的 和 , 可能是相等的。我们可以在枚举时用一个 bool 数组对 进行判重, 避免重复搜索某一个和。
经过观察分析可以发现, 的值(序列长度)不会太大( ),而每次枚举两个数的和,分支很多。所以我们采用迭代加深的搜索方式,从1开始限制搜索深度,若搜索失败就增加深度限制重新搜索,直到找到一组解时即可输出答案。
双向搜索
除了迭代加深之外,双向搜索也可以避免在深层子树上浪费时间。在一些题目中,问题不但具有“初态”,还具有明确的“终态”,并且从初态开始搜索与从终态开始逆向搜索产生的搜索树都能覆盖整个状态空间。在这种情况下,就可以采用双向搜索——从初态和终态出发各搜索一半状态,产生两棵深度减半的搜索树,在中间交会、组合成
最终的答案。
如下图所示,左侧是直接进行一次搜索产生的搜索树,右侧是双向搜索的两棵搜索树,避免了层数过深时分支数量的大规模增长。
【例题】送礼物 TYVJ1340
作为惩罚,小G被遣送去帮助某神牛给女生送礼物(小G:貌似是个好差事),但是在小G看到礼物之后,他就不这么认为了。该神牛有 个礼物,其中第i个礼物的重量是 。小G的力气也异常大,他一次可以搬动重量之和不超过 的任意多个物品。小G希望一次搬掉尽量重的一些物品,请你告诉小G在他的力气范围内一次性能搬动的最大重量是多少。
这道题目就是“子集和”问题的扩展——从给定的 个数中选择几个,使它们的和最接近 。了解“背包”问题的读者可能也已经发现,这道题目还是一个“大体积”的背包问题。这类问题的直接解法就是进行“指数型”的枚举——搜索每个礼物选还是不选,时间复杂度为 。当然,若搜索过程中已选的礼物重量之和已经大于 ,可以及时剪枝。
此题 的复杂度过高。这时我们就可以利用双向搜索的思想,把礼物分成两半。
首先,我们搜索出从前一半礼物中选出若干个,可能达到的 之间的所有重量值,存放在一个数组 中,并对数组 进行排序。
然后,我们进行第二次搜索,尝试从后一半礼物中选出一些。对于每个可能达到的重量值 ,在第一部分得到的数组 中二分查找 的数值中最大的一个,用二者的和更新答案。
这个算法的时间复杂度就只有 了。进一步地,我们还可以加入一些剪枝:
可行性剪枝
在第二次搜索中,如果当前重量 加上 数组中最小的重量已经大于 ,剪枝。
2.优化搜索顺序
把礼物按照重量降序排序后再分半、搜索。