0x66 Tarjan 算法与无向图连通性

无向图的割点与桥

给定无向连通图 $G = (V,E)$

若对于 $x \in V$ ，从图中删去节点 $x$ 以及所有与 $x$ 关联的边之后， $G$ 分裂成两个或两个以上不相连的子图，则称 $x$ 为 $G$ 的割点。

若对于 $e \in E$ ，从图中删去边 $e$ 之后， $G$ 分裂成两个不相连的子图，则称 $e$ 为 $G$ 的桥或割边。

一般无向图（不一定连通）的“割点”和“桥”就是它的各个连通块的“割点”和“桥”。

根据著名计算机科学家 Robert Tarjan 的名字命名的 Tarjan 算法能够在线性时间内求出无向图的割点与桥，进一步可求出无向图的双连通分量（本节后半部分将会介绍）。在有向图方面，Tarjan 算法能够求出有向图的强连通分量、必经点与必经边（下一节将会介绍）。Robert Tarjan 在数据结构方面也做出了很多卓有成效的工作，包括证明并查集的时间复杂度，提出斐波那契堆、Splay Tree 和 Lint-Cut Tree 等。

Tarjan 算法基于无向图的深度优先遍历，在 0x21 节中，我们已经介绍了树与图的深度优先遍历，并引入了“时间戳”的概念。

时间戳

在图的深度优先遍历过程中，按照每个节点第一次被访问的时间顺序，依次给予 $N$

个节点 $1 \sim N$ 的整数标记，该标记就被称为“时间戳”，记为 $dfn[x]$ 。

搜索树

在无向连通图中任选一个节点出发进行深度优先遍历，每个点只访问一次。所有发生递归的边 $(x, y)$ （换言之，从 $x$ 到 $y$ 是对 $y$ 的第一次访问）构成一棵树，我们把它称为“无向连通图的搜索树”。当然，一般无向图（不一定连通）的各个连通块的搜索树构成无向图的“搜索森林”。

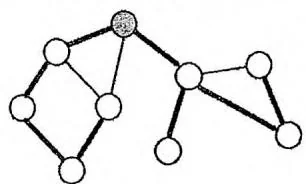
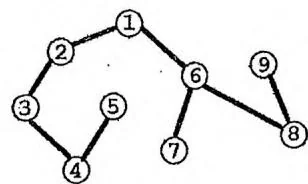
下图左侧展示了一张无向连通图，灰色节点是深度优先遍历的起点，加粗的边是“发生递归”的边（假设我们在遇到多个分支时，总是优先访问最靠左的一条）。右侧展示了深度优先遍历的搜索树，并标注了节点的时间戳。

追溯值

除了时间戳之外，Tarjan算法还引入了一个“追溯值” $low[x]$ 。设 $\operatorname{subtree}(x)$ 表示搜索树中以 $x$ 为根的子树。 $low[x]$ 定义为以下节点的时间戳的最小值：

subtree(x) 中的节点。
通过1条不在搜索树上的边，能够到达 subtree $(x)$ 的节点。

以上图为例。为了叙述简便，我们用时间戳代替节点编号。subtree(2) = {2,3,4,5}。另外，节点1通过不在搜索树上的边（1,5）能够到达subtree(2)。所以 $low[2] = 1$ 。

根据定义，为了计算 $low[x]$ ，应该先令 $low[x] = dfn[x]$ ，然后考虑从 $x$ 出发的每条边 $(x,y)$ ：

若在搜索树上 $x$ 是 $y$ 的父节点，则令 $low[x] = \min (low[x],low[y])$ 。

若无向边 $(x,y)$ 不是搜索树上的边，则令 $low[x] = \min (low[x],dfn[y])$ 。

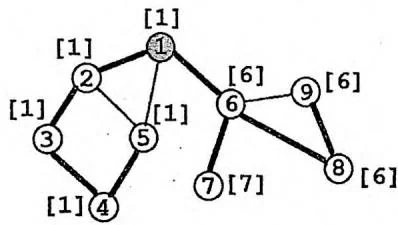
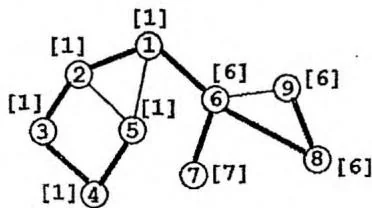
下图的中括号[]里的数值标注了每个节点的“追溯值”low。

割边判定法则

无向边 $(x, y)$ 是桥，当且仅当搜索树上存在 $x$ 的一个子节点 $y$ ，满足：

d f n [ x ] < l o w [ y ]

根据定义， $dfn[x] < low[y]$ 说明从 subtree(y) 出发，在不经过 $(x, y)$ 的前提下，不管走哪条边，都无法到达 $x$ 或比 $x$ 更早访问的节点。若把 $(x, y)$ 删除，则 subtree(y) 就好像形成了一个封闭的环境，与节点 $x$ 没有边相连，图断开成了两部分，因此 $(x, y)$ 是割边。

反之，若不存在这样的子节点 $y$ ，使得 $dfn[x] < low[y]$ ，则说明每个subtree(y)都能绕行其他边到达 $x$ 或比 $x$ 更早访问的节点， $(x,y)$ 自然就不是割边。

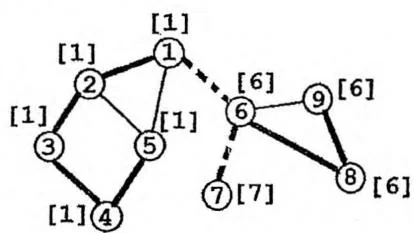
下面的无向图中有两条“桥”边，用虚线标识。读者不难发现，桥一定是搜索树中的边，并且一个简单环中的边一定都不是桥。

下面的程序求出一张无向图中所有的桥。特别需要注意，因为我们遍历的是无向图，所以从每个点 $x$ 出发，总能访问到它的父节点 $fa$ 。根据 low 的计算方法， $(x, fa)$ 属于搜索树上的边，且 $fa$ 不是 $x$ 的子节点，故不能用 $fa$ 的时间戳来更新 $low[x]$ 。

但是，如果仅记录每个节点的父节点，会无法处理重边的情况——当 $x$ 与 $fa$ 之间有多条边时， $(x, fa)$ 一定不是桥。在这些重复的边中，只有一条算是“搜索树上的边”，其他的几条都不算。故有重边时， $dfn[fa]$ 能用来更新 $low[x]$ 。

一个好的解决方案是：改为记录“递归进入每个节点的边的编号”。编号可认为是边在邻接表中存储的下标位置。在0x01和0x13节，我们提到过“成对变换”技巧。把无向图的每条边看作双向边，成对存储在下标“2和3”“4和5”“6和7”……处。若沿着编号为 $i$ 的边递归进入了节点 $x$ ，则忽略从 $x$ 出发的编号为 $i \times \text{or} 1$ 的边，通过其他边计算 $low[x]$ 即可。

const int SIZE = 100010;  
int head[SIZE], ver[SIZE * 2], Next[SIZE * 2];  
int dfn[SIZE], low[SIZE], n, m, tot, num;  
bool bridge[SIZE * 2];  
void add(int x, int y) {

$\begin{array}{l}\text{ver} [ + + \text{tot}] = \text{y},\text{Next} [\text{tot}] = \text{head} [\text{x}],\text{head} [\text{x}] = \text{tot};\\ \end{array}$    
}   
void tarjan(int x, int in_edge) { dfn[x]  $=$  low[x]  $=$  ++num; for (int i  $=$  head[x]; i; i  $=$  Next[i]) { int y  $=$  ver[i]; if (!dfn[y]) { tarjan(y, i); low[x]  $=$  min(low[x], low[y]); if (low[y]  $>$  dfn[x]) bridge[i]  $=$  bridge[i ^ 1]  $=$  true; } else if (i != (in_edge ^ 1)) low[x]  $=$  min(low[x], dfn[y]); }   
}   
int main() { cin >> n >> m; tot  $= 1$  . for (int i  $= 1$  ; i <= m; i++) { int x, y; scanf("%d%d", &x, &y); add(x, y), add(y, x); } for (int i  $= 1$  ; i <= n; i++) if (!dfn[i]) tarjan(i, 0); for (int i  $= 2$  ; i < tot; i += 2) if (bridge[i]) printf("%d%d\n", ver[i ^ 1], ver[i]);

割点判定法则

若 $x$ 不是搜索树的根节点（深度优先遍历的起点），则 $x$ 是割点当且仅当搜索树上存在 $x$ 的一个子节点 $y$ ，满足：

d f n [ x ] \leq l o w [ y ]

特别地，若 $x$ 是搜索树的根节点，则 $x$ 是割点当且仅当搜索树上存在至少两个子节点 $y_{1}, y_{2}$ 满足上述条件。

证明方法与割边的情形类似，这里就不再赘述。在“割边判定法则”画出的例子中，共有2个割点，分别是时间戳为1和6的两个点。

下面的程序求出一张无向图中所有的割点。因为割点判定法则是小于等于号，所以在求割点时，不必考虑父节点和重边的问题，从 $x$ 出发能访问到的所有点的时间戳都可以用来更新 $low[x]$ 。

const int SIZE = 100010;  
int head[SIZE], ver[SIZE * 2], Next[SIZE * 2];  
int dfn[SIZE], low[SIZE], stack[SIZE];  
int n, m, tot, num, root;  
bool cut[SIZE];  
void add(int x, int y) {  
    ver++;  
    ver++;  
    next++;  
    for (int i = head[x]; i = Next[i]) {  
        int y = ver[i];  
        if (!dfn[y]) {  
            char * x;  
            char * y;  
            char * i;  
            char * i++;  
            char * i++;  
            char * i++;  
            char * i++;  
            char * i++;  
            char * i++;  
            char * i++;  
            char * i++;  
            char * i++;  
            char * i++;  
            char * i++;  
            char * i++;  
            char * i++;  
            char * i++;  
            char * i++;  
            char * i++;  
            char * i++;  
            char  $x$  = root;  
            char  $y$  = flag;  
            char  $z$  = true;  
        }  
    else low[x] = min(low[x], dfn[y]);  
}

cin >> n >> m;  
tot = 1;  
for (int i = 1; i <= m; i++) {  
    int x, y;  
    scanf("%d%d", &x, &y);  
    if (x == y) continue;  
    add(x, y), add(y, x);  
}  
for (int i = 1; i <= n; i++)  
    if (!dfn[i]) root = i, tarjan(i);  
for (int i = 1; i <= n; i++)  
    if (cut[i]) printf("%d ", i);  
puts("are cut-vertexes");

【例题】BLO BZOJ1123

Byteotia城市有 $n$ 个城镇， $m$ 条双向道路，其中 $n \leq 10^{5}$ ， $m \leq 5 * 10^{5}$ 。每条道路连接两个不同的城镇，没有重复的道路，所有城镇连通。把城镇看作节点，把道路看作边。容易发现，整个城市构成一张无向图。

你需要输出 $n$ 个整数，其中第 $i$ 个整数表示把与节点 $i$ 关联的所有边去掉之后（不去掉节点 $i$ 本身），无向图中有多少个有序点对 $(x, y)$ ，满足 $x$ 和 $y$ 不连通。

根据割点的定义，若节点 $i$ 不是割点，则把节点 $i$ 关联的所有边去掉之后，只有 $i$ 与其他 $n - 1$ 个节点不连通，而其他 $n - 1$ 个节点之间还是连通的。注意题目求的是有序点对，即 $(x, y)$ 和 $(y, x)$ 算不同的点对，故此时答案为 $2 * (n - 1)$ 。

若节点 $i$ 是割点，则把节点 $i$ 关联的所有边去掉之后，图会分成若干个连通块。我们应该求出这些连通块的大小，两两相乘再相加。在图论的连通性问题中，我们经常要从搜索树的角度来进行分析。设在搜索树上，节点 $i$ 的子节点集合中，有 $t$ 个点 $s_1, s_2, \dots, s_t$ 满足割点判定法则 $dfn[i] \leq low[s_k]$ 。于是，删除 $i$ 关联的所有边后，无向图分成至多 $t + 2$ 个连通块，每个连通块的节点构成情况为：

节点 $i$ 自身单独构成一个连通块。
有 $t$ 个连通块，分别由搜索树上以 $s_k (1 \leq k \leq t)$ 为根的子树中的节点构成。
还可能有一个连通块，由除了上述节点之外的所有点构成。

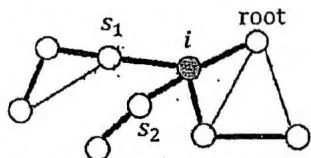
无向连通图和它的搜索树（粗边）在搜索树上 $i$ 有3个子节点其中 $s_1,s_2$ 的low值 $\geq dfn[i]$

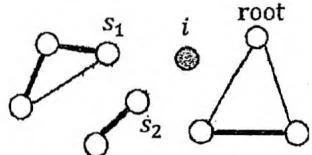
删除节点 $i$ 关联的所有边，无向图分成4个连通块：节点 $i$ 自身、以 $s_1$ 或 $s_2$ 为根的子树中的节点、图中剩余部分

不妨在 Tarjan 算法执行深度优先遍历的过程中，顺便求出搜索树每棵“子树”的大小。设 $size[x]$ 表示以 $x$ 为根的子树大小。综上所述，删掉一个割点 $i$ 之后，不连通的有序对数量为：

\begin{array}{l} \operatorname {s i z e} \left[ s _ {1} \right] * (n - \operatorname {s i z e} [ s _ {1} ]) + \operatorname {s i z e} [ s _ {2} ] * (n - \operatorname {s i z e} [ s _ {2} ]) + \dots + \operatorname {s i z e} [ s _ {t} ] * (n - \operatorname {s i z e} [ s _ {t} ]) \\ + 1 * (n - 1) + \left(n - 1 - \sum_ {k = 1} ^ {t} s i z e [ s _ {k} ]\right) * \left(1 + \sum_ {k = 1} ^ {t} s i z e [ s _ {k} ]\right) \\ \end{array}

const int N = 100010, M = 500010;
int head[N], ver[M * 2], Next[M * 2];
int dfn[N], low[N], Size[N];
long long ans[N];
bool cut[N];
int n, m, tot, num;
void add(int x, int y) {
    ver[++tot] = y, Next[tot] = head[x], head[x] = tot;
}

sum += Size[y]; if (x != 1 || flag > 1) cut[x] = true; } else low[x] = min(low[x], dfn[y]); } if (cut[x]) ans[x] += (long long)(n - sum - 1)*(sum + 1) + (n - 1); else ans[x] = 2 * (n - 1); } int main() { cin >> n >> m; tot = 1; for (int i = 1; i <= m; i++) { int x, y; scanf("%d%d", &x, &y); if (x == y) continue; add(x, y), add(y, x); } tarjan(1); for (int i = 1; i <= n; i++) printf("%1ld\n", ans[i]); }

无向图的双连通分量

若一张无向连通图不存在割点，则称它为“点双连通图”。若一张无向连通图不存在桥，则称它为“边双连通图”。

无向图的极大点双连通子图被称为“点双连通分量”，简记为“v-DCC”①。无向连通图的极大边双连通子图被称为“边双连通分量”，简记为“e-DCC”②。二者统称为“双连通分量”，简记为“DCC”。

在上面的定义中，我们称一个双连通子图 $G' = (V', E')$ “极大”（其中 $V' \subseteq V, E' \subseteq E$ ），是指不存在包含 $G'$ 的更大的子图 $G'' = (V'', E'')$ ，满足 $V' \subseteq V'' \subseteq V, E' \subseteq$

$E'' \subseteq E$ 并且 $G''$ 也是双连通子图。

定理

一张无向连通图是“点双连通图”，当且仅当满足下列两个条件之一：

图的顶点数不超过2。
图中任意两点都同时包含在至少一个简单环中。其中“简单环”指的是不自交的环，也就是我们通常画出的环。

一张无向连通图是“边双连通图”，当且仅当任意一条边都包含在至少一个简单环中。

证明：

该定理给出了无向连通图是“点双连通图”或“边双连通图”的充要条件。我们以“点双连通图”为例进行证明，对于“边双连通图”的证明，请读者自己完成。

对于顶点数不超过2的情况，定理显然成立，下面假设图中顶点数不小于3。

先证充分性。若任意两点 $x, y$ 都同时包含在至少一个简单环中，则 $x, y$ 之间至少有两条不相交的路径。无论从图中删除哪个节点， $x, y$ 均能通过两条路径之一相连。故图中不存在割点，是点双连通图。

再证必要性。反证法，假设一张无向连通图是“点双连通图”，并且存在两点 $x, y$ ，它们不同时处于任何一个简单环中。

如果 $x, y$ 之间仅存在1条简单路径，那么路径上至少有一个割点，与“点双连通”矛盾。

如果 $x, y$ 之间存在2条或2条以上的简单路径，那么容易发现，任意两条都至少有一个除 $x, y$ 之外的交点；进一步可推导出， $x, y$ 之间的所有路径必定同时交于除 $x, y$ 之外的某一点 $p$ （不然就会存在两条没有交点的路径，形成一个简单环，如下图所示）。

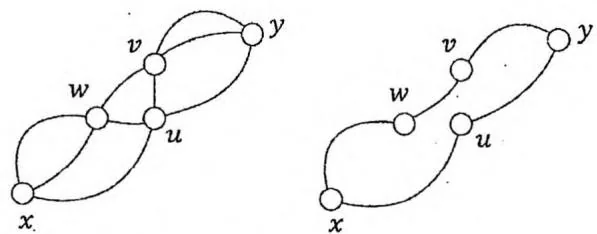
根据定义， $p$ 是一个割点，与“点双连通”矛盾。故假设不成立。

证毕。

边双连通分量(e-DCC)的求法

边双连通分量的计算非常容易。只需求出无向图中所有的桥，把桥都删除后，无向

图会分成若干个连通块，每一个连通块就是一个“边双连通分量”。

下面的无向图共有2条“桥”边，3个“边双连通分量”：

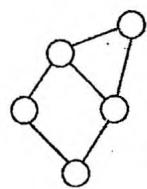
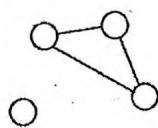
在具体的程序实现中，一般先用 Tarjan 算法标记出所有的桥边。然后，再对整个无向图执行一次深度优先遍历（遍历的过程中不访问桥边），划分出每个连通块。下面的代码在 Tarjan 求桥的参考程序基础上，计算出数组 $c$ ， $c[x]$ 表示节点 $x$ 所属的“边双连通分量”的编号。

int c[SIZE], dcc;  
void dfs(int x) {  
    c[x] = dcc;  
    for (int i = head[x]; i; i = Next[i]) {  
        int y = ver[i];  
        if (c[y] || bridge[i]) continue;  
        dfs(y);  
    }  
}

//以下代码片段加在main函数中  
for(int i = 1; i <= n; i++)  
if (!c[i]) {  
    ++dcc;  
    dfs(i);  
}  
printf("There are %d e-DCCs.\n", dcc);  
for(int i = 1; i <= n; i++)  
printf("%d belongs to DCC %d.\n", i, c[i]);

e-DCC的缩点

把每个 e-DCC 看作一个节点，把桥边 $(x, y)$ 看作连接编号为 $c[x]$ 和 $c[y]$ 的 e-DCC 对应节点的无向边，会产生一棵树（若原来的无向图不连通，则产生森林）。这种把 e-DCC 收缩为一个节点的方法就称为“缩点”。下面的代码在 Tarjan 求桥、求 e-DCC 的参考程序基础上，把 e-DCC 缩点，构成一棵新的树（或森林），存储在另一个邻接表

中。

int hc[SIZE], vc[SIZE * 2], nc[SIZE * 2], tc;  
void add_c(int x, int y) {  
    vc[++tc] = y, nc[tc] = hc[x], hc[x] = tc;  
}  
//以下代码片段加在main函数中  
tc = 1;  
for (int i = 2; i <= tot; i++) {  
    int x = ver[i^1], y = ver[i];  
    if (c[x] == c[y]) continue;  
    add_c(c[x], c[y]);  
}  
printf("缩点之后的森林，点数%d，边数%d（可能有重边）\n", dcc, tc / 2);  
for (int i = 2; i < tc; i++)  
    printf("%d %d\n", vc[i^1], vc[i]);

点双连通分量(v-DCC)的求法

“点双连通分量”是一个极其容易误解的概念。它与前面的例题“BLO”中“删除割点后图中剩余的连通块”是不一样的，请读者格外留意。

若某个节点为孤立点，则它自己单独构成一个v-DCC。除了孤立点之外，点双连通分量的大小至少为2。根据v-DCC定义中的“极大”性，虽然桥不属于任何e-DCC，但是割点可能属于多个v-DCC。还是来看本节一直使用的例子，下面的无向图共有2个割点，4个“点双连通分量”。

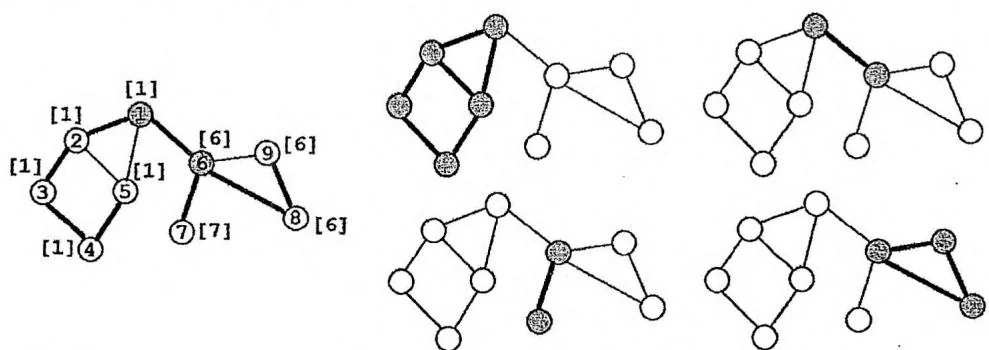
为了求出“点双连通分量”，需要在Tarjan算法的过程中维护一个栈，并按照如下方法维护栈中的元素：

当一个节点第一次被访问时，把该节点入栈。
当割点判定法则中的条件 $dfn[x] \leq low[y]$ 成立时，无论 $x$ 是否为根，都要：

(1) 从栈顶不断弹出节点，直至节点 $y$ 被弹出。
(2) 刚才弹出的所有节点与节点 $x$ 一起构成一个 $\mathbf{v}$ -DCC。

下面的程序在求出割点的同时，计算出 vector 数组 $dcc$ ， $dcc[i]$ 保存编号为 $i$ 的 v-DCC 中的所有节点。

void tarjan(int x) {
    dfn[x] = low[x] = ++num;
    stack[++top] = x;
    if (x == root && head[x] == 0) { // 孤立点
        dcc[++cnt].push_back(x);
        return;
    }
    int flag = 0;
    for (int i = head[x]; i; i = Next[i]) {
        int y = ver[i];
        if (!dfn[y]) {
            tarjan(y);
            low[x] = min(low[x], low[y]);
            if (low[y] >= dfn[x]) {
                flag++;
                if (x != root || flag > 1) cut[x] = true;
                cnt++;
                int z;
                do {
                    z = stack[top--];
                    dcc[cnt].push_back(z);
            } while (z != y);
            dcc[cnt].push_back(x);
        }
    }
    else low[x] = min(low[x], dfn[y]);
}

// 以下代码片段加在求割点程序的 main 函数中
for (int i = 1; i <= cnt; i++) {
printf("e-DCC %d:", i);
for (int j = 0; j < dcc[i].size(); j++)

printf("%d", dcc[i][j]); puts("");

$\mathbf{v}$ -DCC的缩点

v-DCC的缩点比e-DCC要复杂一些——因为一个割点可能属于多个v-DCC。设图中共有 $p$ 个割点和 $t$ 个v-DCC。我们建立一张包含 $p + t$ 个节点的新图，把每个v-DCC和每个割点都作为新图中的节点，并在每个割点与包含它的所有v-DCC之间连边。容易发现，这张新图其实是一棵树（或森林），如下图所示：

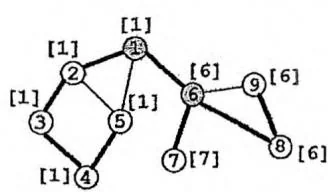
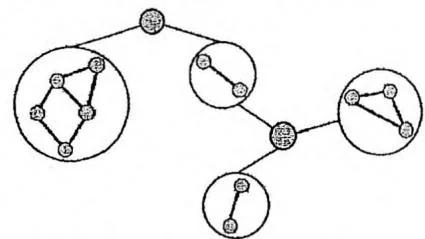
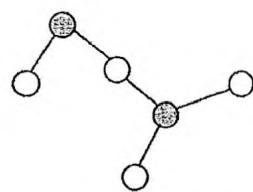
下面的代码在 Tarjan 求割点和 v-DCC 的参考程序的 main 函数基础上，对 v-DCC 缩点，构成一棵新的树（或森林），存储在另一个邻接表中。

// 给每个割点一个新的编号（编号从 cnt+1 开始）

num = cnt;  
for (int i = 1; i <= n; i++)  
    if (cut[i]) new_id[i] = ++num;  
// 建新图，从每个 v-DCC 到它包含的所有割点连边  
tc = 1;  
for (int i = 1; i <= cnt; i++)  
    for (int j = 0; j < dcc[i].size(); j++) {  
        int x = dcc[i][j];  
        if (cut[x]) {  
            add_c(i, new_id[x]);  
            add_c(new_id[x], i);  
        }  
    else c[x] = i; // 除割点外，其他点仅属于 1 个 v-DCC  
}  
printf("缩点之后的森林，点数 %d，边数 %d\n", num, tc / 2)  
printf("编号 1~%d 的为原图的 v-DCC，编号 >%d 的为原图割点\cnt, cnt);  
for (int i = 2; i < tc; i += 2)  
    printf("%d %d\n", vc[i^1], vc[i]);

读者将在0x6B节的习题中运用e-DCC与v-DCC的缩点，结合倍增LCA算法，多次回答无向图上两点之间的必经边、必经点的询问。

【例题】Network POJ3694

给定一张 $N$ 个点 $M$ 条边的无向连通图，然后执行 $Q$ 次操作，每次向图中添加一条边，并且询问当前无向图中“桥”的数量。 $N \leq 10^{5}, M \leq 2 * 10^{5}, Q \leq 1000$ 。

先用Tarjan算法求出无向图中所有的“边双连通分量”(e-DCC)，并对每个e-DCC缩点，得到一棵树，树上的每个节点都是原图中的一个e-DCC。设 $c[x]$ 表示节点 $\pmb{x}$ 所在的e-DCC的编号。最初，“桥”的总数就是缩点之后树的边数。

依次考虑每个添加边 $(x,y)$ 的操作。若 $x,y$ 属于同一个e-DCC $(c[x] = c[y])$ ，则加入该边后，无向图中“桥”的数量不变。

若 $x, y$ 属于不同的 e-DCC，则在缩点后得到的树上， $c[x]$ 与 $c[y]$ 之间的路径上的每条边都不再是“桥”，因为它们都处在一个环内。我们可以求出 $p = \operatorname{LCA}(c[x], c[y])$ ，从 $c[x]$ 不断走向父节点，直至点 $p$ ，把经过的边都标记成“不再是桥”。从 $c[y]$ 开始也执行一样的标记过程。若有 cnt 条边新获得了标记，则把图中“桥”的总数减掉 cnt 即可。

上述算法的时间复杂度为 $O(M + Q*N)$ ，但本题数据比较宽松，可以得到满分。我们也可以用并查集进一步优化，当树上每条边获得“不再是桥”的标记后，就把这条边的子节点所在的集合合并到父节点所在的集合中。这样一来，从 $c[x]$ 走向 $\operatorname{LCA}(c[x], c[y])$ 时，每一步可以直接走到并查集的 get 函数返回的节点上，本质上是利用并查集对“不再是桥”的边进行了路径压缩。时间复杂度可以降低到 $O(M + Q\log N)$ 。

【例题】Knights of the Round Table POJ2942

国王要在圆桌上召开骑士会议，但是有若干对骑士之间互相憎恨。出于各种各样奇怪的原因，每次开会都必须有如下要求：

相互憎恨的两个骑士不能坐在相邻的两个位置；
为了让投票表决议题时都能有结果（不平票），出席会议的骑士数必须是奇数。

如果有某个骑士无法出席任何会议，则国王会为了世界和平把他踢出骑士团。

现在给定骑士总数 $n(n \leq 1000)$ ，以及 $m(m \leq 10^6)$ 对相互憎恨的关系，求至少要踢掉多少个骑士。

我们可以建出原图的“补图”—— $n$ 个节点代表 $n$ 个骑士，若两名骑士没有憎恨关系，则在二者之间连一条无向边。

根据题意，若干名骑士可以召开圆桌会议的条件是：它们对应的节点组成一个长度为奇数的简单环（简称奇环）。因此，本题就是求有多少个点不被任何奇环包含，这些点就是应该被踢掉的骑士。

引理1：

若两个骑士属于两个不同的“点双连通分量”，则他们不可能一起出席会议。

证明：

反证法。假设 $x, y$ 分别属于编号为 $c[x]$ 和 $c[y]$ 的 v-DCC，其中 $c[x] \neq c[y]$ ，并且 $x, y$ 处于某一个奇环中（能出席会议）。因为一个 v-DCC 中不包含割点，所以无论删掉图中哪个点， $x$ 与编号为 $c[x]$ 的 v-DCC 中其他点仍然连通， $y$ 与编号为 $c[y]$ 的 v-DCC 中其他点也仍然连通。而 $x, y$ 处于一个环中，环不存在割点，无论删除哪个点， $x, y$ 之间也是连通的。

综上所述，无论删除哪个点，编号为 $c[x]$ 和 $c[y]$ 的两个v-DCC中的点都仍然是连通的。换言之，这两个v-DCC合在一起构成的图中不存在割点，也是v-DCC。这与v-DCC的“极大性”矛盾。故假设不成立，原命题成立。

证毕。

引理2：

若某个“点双连通分量”中存在奇环，则这个“点双连通分量”中的所有点都被至少一个奇环包含。

证明：

设 v-DCC 中的奇环依次由节点 $v_{1}, v_{2}, \cdots, v_{t}$ 构成， $t$ 为奇数。容易发现，对于奇环以外的任意节点 $x$ ，奇环上必然存在两点 $v_{i}, v_{j}$ ，满足 $x, v_{i}, v_{j}$ 三个点都在某个简单环上。否则我们就有办法删除环上的一个点，让 $x$ 与奇环不连通。

进一步，我们一定可以构造出如右图所示的包含 $x, v_{i}, v_{j}$ 三个点的简单环。在这个环上，无论 $x$ 到 $v_{i}$ 的路径长度加上 $x$ 到 $v_{j}$ 的路径长度是奇数还是偶数，因为奇环上从 $v_{i}$ 到 $v_{j}$ 有两条长度的奇偶性不同的路径，所以总能拼出包含 $x$ 的奇环。

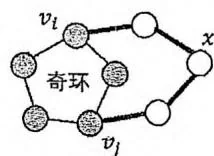
证毕。

综上所述，用Tarjan算法求出“补图”中所有的v-DCC，判定每个v-DCC中是否存在奇环即可。若存在奇环，则该v-DCC中的所有骑士都可以参加会议（都在某个奇环中）。

奇环可以用深度优先遍历的染色法进行判定。一张无向图没有奇环，等价于它是一张二分图。我们将在0x68节讲解二分图（奇环）的判定方法，不熟悉的读者可提前阅

读0x68节开头部分的内容。

$\spadesuit$ 欧拉路问题

在本节最后，我们抛开 Tarjan 算法，探讨一个关于无向图连通性的小问题——欧拉路问题，俗称“一笔画”问题。

给定一张无向图，若存在一条从节点 $S$ 到节点 $T$ 的路径，恰好不重不漏地经过每条边一次（可以重复经过图中的节点），则称该路径为 $S$ 到 $T$ 的欧拉路。

特别地，若存在一条从节点 $S$ 出发的路径，恰好不重不漏地经过每条边一次（可以重复经过图中的节点），最终回到起点 $S$ ，则称该路径为欧拉回路。存在欧拉回路的无向图被称为欧拉图。

欧拉图的判定

一张无向图为欧拉图，当且仅当无向图连通，并且每个点的度数都是偶数。

欧拉路的存在性判定

一张无向图中存在欧拉路，当且仅当无向图连通，并且图中恰好有两个节点的度数为奇数，其他节点的度数都是偶数。这两个度数为奇数的节点就是欧拉路的起点 $S$ 和终点 $T$ 。

在判定无向图存在欧拉回路后，我们可以借助深度优先遍历和栈，求出欧拉回路的一种具体方案。流程如下：

void dfs(int x)  
对于从  $x$  出发的每条边  $(x,y)$  如果该边没有被访问过把这条边标记为已访问dfs(y)把y入栈  
在主函数中dfs(1)倒序输出栈中所有节点

欧拉图每个节点度数为偶数说明：只要到达一个节点，就必定有一条尚未走过的边可以离开该点。故在上面的伪代码中，调用 $dfs(1)$ ，不断递归，每次都走到“从 $x$ 出发的第一条未访问的边”的另一端点 $y$ ，最终一定能回到节点 1，产生一条回路。如下页图所示：

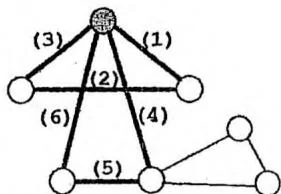
当然，这条回路不能保证经过了图中的每条边。所以 $dfs$ 函数会继续考虑从 $x$ 出发的其他未访问的边，找到第二条回路。如下图所示：

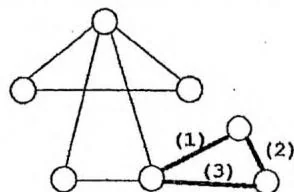
上述伪代码实际上找出了若干条回路。我们需要把这些回路按适当的方法拼接在一起，形成整张图的欧拉回路。一个很显然的拼接方法就是把第二条回路嵌入第一条回路中间，如下图所示：

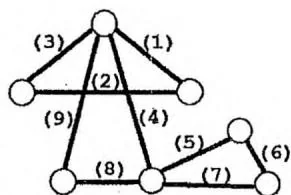
上面伪代码中维护的栈，恰好替我们完成了这个拼接工作。最后，把栈里的所有节点倒序输出，就得到了一条欧拉回路。

值得提醒的是，上述算法的时间复杂度为 $O(NM)$ 。因为一个点会被重复遍历多次，每次都会扫描与它相连的所有的边——虽然我们明明知道大部分边已经访问过了。

假设我们采用邻接表存储无向图，我们可以在访问一条边 $(x, y)$ 后，及时修改表头 $head[x]$ ，令它指向下一条边。这样我们每次只需取出 $head[x]$ ，就自然跳过了所有已经访问过的边。

另外，因为欧拉回路DFS的递归层数是 $O(M)$ 级别，容易造成系统栈溢出。我们可以用另一个栈，模拟机器的递归过程，把代码转化为非递归实现。

加入上述优化后的完整程序如下，其时间复杂度为 $O(N + M)$ 。

int head[100010], ver[1000010], Next[1000010], tot; // 邻接表

int stack[1000010], ans[1000010]; // 模拟系统栈，答案栈

bool vis[1000010];

int n, m, top, t;

void add(int x, int y) {

$\begin{array}{l}\text{ver} [ + + \text{tot}] = \text{y},\text{Next} [\text{tot}] = \text{head} [\text{x}],\text{head} [\text{x}] = \text{tot};\\ \end{array}$    
void-euler(){stack[++top]  $= 1$  ·while  $(\mathrm{top} > 0)$  {int  $\mathbf{x} =$  stack[top],i  $=$  head[x];while (i && vis[i]) i  $=$  Next[i]; //找到一条尚未访问的边if(i){//沿着这条边模拟递归过程，标记该边，并更新表头stack[++top]  $=$  ver[i];vis[i]  $=$  vis[i^1]  $=$  true;head[x]  $=$  Next[i];}else{//x相连的所有边均已访问，模拟回溯过程，并记在答案栈中top--;ans[++t]  $= x$  ：  
1  
1  
int main() {cin>>n>>m;tot  $= 1$  ·for(inti  $= 1$  ;i<=m;i++) {intx,y;scanf("%d%d",&x,&y);add(x,y),add(y,x);）euler();for(inti  $= t$  ;i；i--）printf("%d\n"，ans[i]);

【例题】Watchcow FOJ2230

给定 $N$ 个点 $M$ 条边的无向图 $(1 \leq N \leq 10^{4}, 1 \leq M \leq 5 * 10^{4})$ , 求一条路径, 从节点 1 出发, 最后回到节点 1 , 并且满足每条边恰好被沿着正、反两个方向分别经过一次。若有多种方案, 输出任意一种即可。

我们只需在求欧拉回路的参考程序中，去掉对每条边的 vis 标记，即可得到本题的解答。这是因为，按照一般的存储方式，每条无向边在邻接表中会以正、反两个方向

分别保存一次。若没有 vis 标记，则根据表头数组 head 的更新方法，每条无向边会被正、反各经过一次，恰好符合题目要求。

0x66_Tarjan算法与无向图连通性