0x64基环树

众所周知， $N$ 个点的树有 $N - 1$ 条边。若在树上任意添加一条边，则会形成一个环。除了环之外，其余部分由若干棵子树构成。

我们把这种 $N$ 个点 $N$ 条边的连通无向图，即在树上加一条边构成的恰好包含一个环的图，称为“基环树”。如果不保证连通，那么 $N$ 个点 $N$ 条边的无向图也可能是若干棵基环树组成的森林，简称为“基环树森林”。

在有向图中，我们也有类似的概念。 $N$ 个点、 $N$ 条边、每个节点有且仅有一条入边的有向图就好像以“基环”为中心，有向外扩展的趋势，故称为“外向树”。 $N$ 个点、 $N$ 条边、每个节点有且仅有一条出边的有向连通图就好像以“基环”为中心，有向内收缩的趋势，故称为“内向树”。外向树和内向树也经常统称为“基环树”。如果不保证连通，那么 $N$ 个点、 $N$ 条边、每个节点有且仅有一条出（入）边的有向图也可能是“内（外）向树森林”的形态。

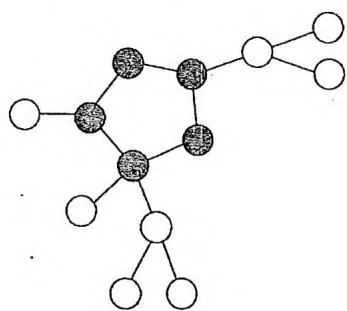
基环树（ $N$ 个点 $N$ 条边的连通无向图）

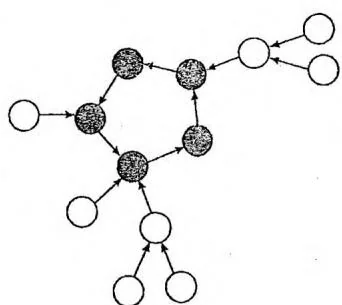
内向树（每个点有且仅有1条出边）

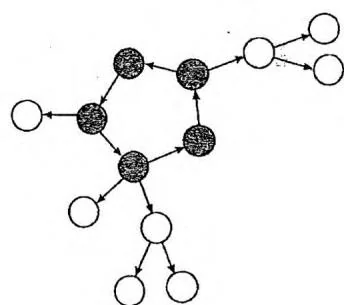
外向树（每个点有且仅有1条入边）

基环树的结构仍然很简单，但比树要复杂些，因此常作为一些经典模型的扩展，以适当增加题目的难度。例如基环树的直径、基环树两点之间的距离、基环树动态规划等。无论哪种模型，求解基环树相关问题的方法一般都是先找出图中唯一的环，把环作为基环树的广义“根节点”，把除了环之外的部分按照若干棵树处理，再考虑与环一起计算。

【例题】岛屿 IOI2008/BZOJ1791

你准备游览一个公园，该公园由 $N$ 个岛屿组成，当地管理部门从每个岛屿出发向另外一个岛屿建了一座桥，不过桥是可以双向行走的。同时，每对岛屿之间都有一艘专用的往来两岛之间的渡船。相对于乘船而言，你更喜欢步行。你希望经过的桥的总长度尽可能长，但受到以下的限制：

1. 可以自行挑选一个岛开始游览。

2. 任何一个岛都不能游览一次以上。

3. 无论任何时间, 你都可以由当前所在的岛 $S$ 去另一个从未到过的岛 $D$ 。从 $S$ 到 $D$ 有以下方法:

(1) 步行。仅当两个岛之间有一座桥时才有可能。对于这种情况, 桥的长度会累加到你步行的总距离中。

(2) 渡船。你可以选择这种方法，仅当没有任何桥和以前使用过的渡船的组合可以由 $S$ 走到 $D$ （当检查是否可到达时，你应该考虑所有的路径，包括经过你曾游览过的那些岛）。

注意，你不必游览所有的岛，也可能无法走完所有的桥。

请你编写一个程序, 给定 $N$ 座桥以及它们的长度, 按照上述的规则, 计算你可以走过的桥的长度之和的最大值。

数据范围： $2\leq N\leq 10^{6}$

先来定义基环树的直径。基环树中最长的简单路径被称为基环树的最长链，其长度被称为基环树的直径。这里，简单路径指的是不自交（不重复经过任何点或边）的路径。

根据题意，整个公园是一个基环树森林的形态。按照题目中给出的乘坐渡船的规则，一旦离开某棵基环树，就不能再通过渡船回来。因此，这道题目的答案就是各棵基环树的直径之和。

如何求出基环树的最长链呢？显然，基环树的最长链可能有两种情况：

1. 在去掉“环”之后的某棵子树中。

2.经过“环”，其两端分别在去掉“环”上所有边之后的两棵不同子树中。

我们先用一次深度优先遍历找出基环树中的“环”，把“环”上的节点做上标记。设环上的节点为 $s_1, s_2, \dots, s_t$ 。

从每个 $s_i$ 出发，在不经过环上其他节点的前提下，再次执行深度优先遍历，即可访问去掉“环”之后以 $s_i$ 为根的子树。在这样的每棵子树中，按照求树的直径的方法进行DP并更新答案，即可处理第一种情况。同时，还可以计算出 $D[s_i]$ ，表示从节点 $s_i$ 出发走向以 $s_i$ 为根的子树，能够到达的最远节点的距离。

最后，我们考虑第二种情况。这相当于找到环上两个不同的节点 $s_i, s_j$ ，使得 $D[s_i] + D[s_j] + \mathrm{dist}(s_i, s_j)$ 最大。其中 $\mathrm{dist}(s_i, s_j)$ 表示 $s_i, s_j$ 在环上的距离，有逆时针、

顺时针两种走法，取较长的那一种。这等价于我们之前在 $0 \times 55$ 节探讨过的例题“环路运输”，把环断开成链再复制一倍，用单调队列即可在 $O(N)$ 的时间内解决。

【例题】创世纪 TVXJ1940

上帝手中有 $N(N \leq 10^{6})$ 种世界元素，每种元素可以限制另外 1 种元素，把第 $i$ 种世界元素能够限制的那种世界元素记为 $A[i]$ 。现在，上帝要把它们中的一部分投放到一个新的空间中去建造世界。为了世界的和平与安宁，上帝希望所有被投放的世界元素都有至少一个没有被投放的世界元素限制它。上帝希望知道，在此前提下，他最多可以投放多少种世界元素？

把每种世界元素作为图中的节点，从每种元素 $i$ 向它限制的元素 $A[i]$ 连一条有向边。显然，每种世界元素对应的节点都恰好有1条出边，所以这张有向图构成内向树森林。

内向树森林中各棵内向树是独立的，可以分别考虑。对于每棵内向树，可以用一次深度优先遍历找出树中唯一的环。任取环上一点 $p$ ，断开 $p$ 到 $A[p]$ 的有向边（令 $A[p] = 0$ ），内向树就变为了一棵以 $p$ 为根的树，每个 $A[i]$ 就是 $i$ 的父节点。

在一棵树上求解本题，类似于我们之前在 $0 \times 54$ 节探讨过的例题“没有上司的舞会”。设 $F[x,0]$ 表示在不投放元素 $x$ 的情况下，以 $x$ 为根的子树中最多能投放多少种元素。 $F[x,1]$ 表示在投放元素 $x$ 的情况下，以 $x$ 为根的子树中最多能投放多少种元素。

$x$ 不投放时，它的子节点随意，可投放、可不投放：

$x$ 被投放时，至少有一个子节点 $y$ 限制 $x$ ，不能投放，其余子节点随意：

断开 $p$ 到 $A[p]$ 的有向边，在以 $p$ 为根的树上求出的结果就是 $\max (F[p,0],F[p,1])$ 。该结果与原来内向树上的答案只有一点区别——没有利用“ $p$ 可以限制 $A[p]$ ”这条关系。为了弥补这个差别，我们就让 $p$ 强制限制 $A[p]$ ，在以 $p$ 为根的树上重新进行一次树形DP，DP过程中计算 $F[A[p],1]$ 时，让 $A[p]$ 的子节点随意选择投放或不投放，不需要有至少一个子节点限制它（因为它已经被 $p$ 限制）。DP完成后，只用 $F[p,0]$ 更新答案（ $p$ 已经用于限制 $A[p]$ ，不能被投放）。

这种用两次树形DP代替基环树DP的方法，就是我们之前在0x55节提到的“环形DP”的解决方案之一，“两次DP，一次断开，一次强制连接（通过适当的条件和赋

值实现）”。读者可以顺便回顾0x55节的“Naptime”这道例题。

【例题】Freda的传呼机 TYVJ2019

为了随时与 Rainbow 快速交流，Freda 制造了两部传呼机。Freda 和 Rainbow 所在的地方有 $N$ 座房屋、 $M$ 条双向光缆。每条光缆连接两座房屋，传呼机发出的信号只能沿着光缆传递，并且传呼机的信号从第 $i$ 条光缆的其中一端传递到另一端需要花费 $t_i$ 单位时间。

现在 Freda 要进行 $Q$ 次试验，每次选取两座房屋，并想知道传呼机的信号在这两座房屋之间传递至少需要多长时间。请你帮帮他们吧。

$N$ 座房屋通过光缆一定是连通的，并且这 $M$ 条光缆有以下三类连接情况：

1. 光缆不形成环，也就是光缆仅有 $N - 1$ 条。

2. 光缆只形成一个环，也就是光缆仅有 $N$ 条。

3. 每条光缆仅在一个环中（这种情况超出我们的讨论范围，不要求解答）。

数据范围： $2\leq N,M,Q\leq 12000$

第一类数据中的房屋和光缆构成一棵树的结构，光缆的传递时间 $t_i$ 就是边的长度。任选一个节点为根，用一次广度优先遍历预处理出倍增LCA算法的 $F$ 数组，同时计算出根节点到每个节点 $x$ 的距离 $D[x]$ 。于是，对于树中任意两点 $x, y$ ，在二者之间传递信号的时间就是 $D[x] + D[y] - 2 * D[\mathrm{LCA}(x, y)]$ 。

第二类数据中的房屋和光缆构成一棵基环树。在前面两道例题中，我们已经积累了足够的处理基环树的经验，读者应该能够从容应对。先找出“环”，设环上节点为 $s_1, s_2, \dots, s_t$ ，然后对去掉“环”之后剩下的每棵子树，以子树与环的交点 $s_i$ 为根，执行倍增LCA的预处理。

对于每次试验选取的房屋 $x, y$ ，用类似于倍增LCA的查询方法，把 $x, y$ 向上移动。若 $x, y$ 在移动到环之前就相会了，则说明 $x, y$ 来自同一棵子树，相会点就是 $\operatorname{LCA}(x, y)$ ，按照树上的公式来计算 $x, y$ 的距离即可。

若 $x, y$ 分别移动到了环上的 $s_i, s_j$ 两点，则 $x, y$ 之间的最短路径就由子树中 $x$ 到 $s_i$ 、环上 $s_i$ 到 $s_j$ 、子树中 $s_j$ 到 $y$ 三部分组成。 $x$ 到 $s_i$ 的长度就是 $D[x]$ ， $s_j$ 到 $y$ 的长度就是 $D[y]$ 。 $s_i$ 到 $s_j$ 有顺时针和逆时针两种走法，应该取较短的一边。

在考虑每对 $x, y$ 之前，可以预处理出从 $s_1$ 沿着固定方向依次走到环上各点 $s_2, \dots, s_t$ 的距离 $G[s_i]$ （相当于一个前缀和），即可直接计算出环上 $s_i$ 到 $s_j$ 的两种走法哪一边比较短： $\min \left(|G[s_i] - G[s_j]|, L - |G[s_i] - G[s_j]|\right)$ ，其中 $L$ 表示环的总长度。

题目中第三类连接情况，即每条边至多仅在一个环中的无向图，被称为“边仙人掌”。类似地，每个点至多仅在一个环中的无向图被称为“点仙人掌”。点仙人掌一定

是边仙人掌，故我们一般把“点仙人掌”简称为“仙人掌图”。仙人掌图超出了我们的讨论范围，学有余力的读者可以尝试继续解决本题的第三类数据。