8._三元非齐次线性方程组

三元非齐次线性方程组

通过上一节的讨论知道, 对于含有三个方程的三元齐次线性方程组的解的情况可以通过系数矩阵的行列式进行判断, 这一节我们将学习如何判断含有三个方程的三元非齐次线性方程组的解的情况. 在阅读本节前，最好已经了解齐次线性方程解的结构

齐次方程与非齐次方程：方程等号右边全为零的方程叫齐次方程，否则叫非齐次方程

例 解线性方程组

{x1+4x2+2x3=5,2x2+x3=2,x1−2x2−x3=−1.\left\{\begin{aligned} x_1+4 x_2+2 x_3 & =5, \\ 2 x_2+x_3 & =2, \\ x_1-2 x_2-x_3 & =-1 . \end{aligned}\right.

解: 对方程组的增广矩阵作行初等变换:

(142502120000)→(−2)r2+r1(100102120000).\begin{aligned} & \left(\begin{array}{lll|l} 1 & 4 & 2 & 5 \\ 0 & 2 & 1 & 2 \\ 0 & 0 & 0 & 0 \end{array}\right) \xrightarrow{(-2) r_2+r_1}\left(\begin{array}{lll|l} 1 & 0 & 0 & 1 \\ 0 & 2 & 1 & 2 \\ 0 & 0 & 0 & 0 \end{array}\right) . \\ & \end{aligned}

因此,还原方程为

{x1=12x2+x3=2\left\{\begin{array}{l} x_1=1 \\ 2 x_2+x_3=2 \end{array}\right.

选取 x3x_3 为自由未知量, 当 x3x_3 的值取定后, 线性方程组的解也随之确定. 由 x3x_3 取值的任意性可以知道, 这个线性方程组有无穷多个解.

由三元非齐次线性方程组的解可能有三种情况, 分别是无解、唯一解和无穷多个解. 分别讨论如下.

例对于一个三元非齐次线性方程组

{a11x1+a12x2+a13x3=b1,a21x1+a22x2+a23x3=b2,a31x1+a32x2+a33x3=b3,\left\{\begin{array}{l} a_{11} x_1+a_{12} x_2+a_{13} x_3=b_1, \\ a_{21} x_1+a_{22} x_2+a_{23} x_3=b_2, \\ a_{31} x_1+a_{32} x_2+a_{33} x_3=b_3, \end{array}\right.

令 αi=(ai1,ai2,ai3,bi)T,βi=(ai1,ai2,ai3)T\boldsymbol{\alpha}_i=\left(a_{i 1}, a_{i 2}, a_{i 3}, b_i\right)^{\mathrm{T}}, \boldsymbol{\beta}_i=\left(a_{i 1}, a_{i 2}, a_{i 3}\right)^{\mathrm{T}}, 其中 i=1,2,3i=1,2,3. 对这个方程组的增广矩阵作行初等变换, 得到以下三种情形.

情形1

如果三元非齐次线性方程组化为阶梯形方程组如下:

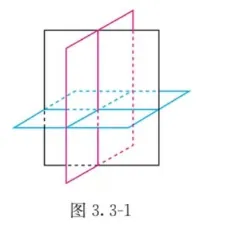
{x1+c12x2+c13x3=d1,x2+c23x3=d2,x3=d3,...(1)\left\{\begin{aligned} x_1+c_{12} x_2+c_{13} x_3 & =d_1, \\ x_2+c_{23} x_3 & =d_2, \\ x_3 & =d_3, \end{aligned}\right. ...(1)

那么这个三元非齐次线性方程组有唯一解. 这时, 方程组（1）所对应的三个平面相交于一点, 如图 3. 3-1 所示. 图片

情形2

如果三元非齐次线性方程组化为阶梯形方程组如下:

{x1+c13x3=d1,x2+c23x3=d2,0=0,...(2)\left\{\begin{aligned} x_1 \quad+c_{13} x_3 & =d_1, \\ x_2+c_{23} x_3 & =d_2, \\ 0 & =0, \end{aligned}\right. ...(2)

或者

{x1+c12x2+c13x3=d1,0=0,0=0,...(3)\left\{\begin{aligned} x_1+c_{12} x_2+c_{13} x_3 & =d_1, \\ 0 & =0, \\ 0 & =0, \end{aligned}\right. ...(3)

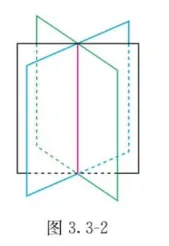
那么这个三元非齐次线性方程组有无穷多个解. 对于经过行初等变换得到方程组 (2) 的情况, 如果向量 α1,α2\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, α3\boldsymbol{\alpha}_3 两两线性无关，那么方程组（1）所对应的三个平面相交于一条直线,如图 3. 3-2 所示;

如果向量 α1,α2,α3\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \boldsymbol{\alpha}_3 中存在两个向量线性相关, 那么方程组 (1) 所对应的三个平面的位置关系为两个平面重合, 第三个平面与这个重合平面交于一条直线.

如果经过行初等变换得到方程组 (3), 那么说明方程组 (1) 所对应的三个平面重合. 图片

情形3

如果三元非齐次线性方程组化为阶梯形方程组如下:

{x1+c13x3=d1,x2+c23x3=d2,0=d3,...(4)\left\{\begin{aligned} x_1 \quad+c_{13} x_3 & =d_1, \\ x_2+c_{23} x_3 & =d_2, \\ 0 & =d_3, \end{aligned}\right. ...(4)

其中 d3≠0d_3 \neq 0, 或者

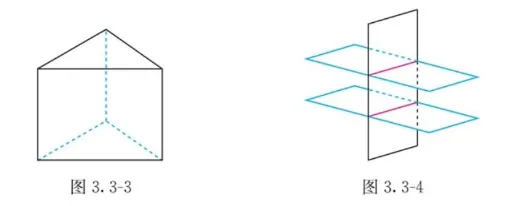
{x1+c12x2+c13x3=d1,0=d2,0=0,...(5)\left\{\begin{aligned} x_1+c_{12} x_2+c_{13} x_3 & =d_1, \\ 0 & =d_2, \\ 0 & =0, \end{aligned}\right. ...(5)

其中 d2≠0d_2 \neq 0, 那么这个三元非齐次线性方程组无解.经过行初等变换后得到方程组（4）时, 若 β1,β2,β3\boldsymbol{\beta}_1, \boldsymbol{\beta}_2, \boldsymbol{\beta}_3 两两线性无关, 则方程组 (1)所对应的三个平面没有公共点, 且两两之间不平行, 如图 3. 3-3 所示; 若 β1,β2,β3\boldsymbol{\beta}_1, \boldsymbol{\beta}_2, \boldsymbol{\beta}_3 存在两个向量线性相关, 则方程组（1）所对应的三个平面中, 有两个平面平行, 第三个平面与它们相交, 如图 3. 3-4 所示.

经过行初等变换后得到方程组（5）时, 若 α1,α2,α3\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \boldsymbol{\alpha}_3 两两线性无关, 则方程组 （1）所对应的三个平面互相平行, 没有公共点; 若

α1,α2,α3\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \boldsymbol{\alpha}_3 存在两个向量线性相关,则方程组 (1) 所对应的三个平面中, 有两个平面重合, 第三个平面与它们平行. 图片

我们已经知道, 齐次线性方程组的通解可以表示为基础解系的线性组合, 下面学习非齐次线性方程组解的结构.

利用向量的加法运算和数乘运算, 可以把三元非齐次线性方程组 Ax=b\boldsymbol{A} \boldsymbol{x}=\boldsymbol{b} 写成向量形式 x1α1+x2α2+x3α3=bx_1 \boldsymbol{\alpha}_1+x_2 \boldsymbol{\alpha}_2+x_3 \boldsymbol{\alpha}_3=\boldsymbol{b}, 其中 αi=(ai1,ai2,ai3)T(i=1,2,3)\boldsymbol{\alpha}_i=\left(a_{i 1}, a_{i 2}, a_{i 3}\right)^{\mathrm{T}}(i=1,2,3) 分别是方程组系数矩阵的列向量, 那么, 三元非齐次线性方程组解的情形如下.

情形 1 在 R\mathbf{R} 中非齐次线性方程组 x1α1+x2α2+x3α3=bx_1 \boldsymbol{\alpha}_1+x_2 \boldsymbol{\alpha}_2+x_3 \boldsymbol{\alpha}_3=\boldsymbol{b} 有唯一解当且仅当 b\boldsymbol{b} 可以由 α1,α2,α3\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \boldsymbol{\alpha}_3 线性表出, 且表示法唯一.

情形 2 在 R\mathbf{R} 中非齐次线性方程组 x1α1+x2α2+x3α3=bx_1 \boldsymbol{\alpha}_1+x_2 \boldsymbol{\alpha}_2+x_3 \boldsymbol{\alpha}_3=\boldsymbol{b} 有无穷多个解当且仅当 b\boldsymbol{b}可以由 α1,α2,α3\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \boldsymbol{\alpha}_3 线性表出, 且表示法有无穷多种.

这样, 就把线性方程组有没有解的问题归结为：常数项列向量 b\boldsymbol{b} 能不能由系数矩阵的列向量组线性表出.

情形 3 在 R\mathbf{R} 中非齐次线性方程组 x1α1+x2α2+x3α3=bx_1 \boldsymbol{\alpha}_1+x_2 \boldsymbol{\alpha}_2+x_3 \boldsymbol{\alpha}_3=\boldsymbol{b} 无解当且仅当 b\boldsymbol{b} 不能由 α1,α2,α3\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \boldsymbol{\alpha}_3 线性表出.

例 在 R3\mathbf{R}^3 中, 设四个向量分别为

α1=(12−3),α2=(5−512),α3=(1−36),β=(2−13), \boldsymbol{\alpha}_1=\left(\begin{array}{c} 1 \\ 2 \\ -3 \end{array}\right), \boldsymbol{\alpha}_2=\left(\begin{array}{c} 5 \\ -5 \\ 12 \end{array}\right), \boldsymbol{\alpha}_3=\left(\begin{array}{c} 1 \\ -3 \\ 6 \end{array}\right), \boldsymbol{\beta}=\left(\begin{array}{c} 2 \\ -1 \\ 3 \end{array}\right) \text {, }

判断 β\boldsymbol{\beta} 是否能由向量组 α1,α2,α3\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \boldsymbol{\alpha}_3 线性表出; 如果能, 写出一种表出方式. 解：判断 β\boldsymbol{\beta} 是否由向量组 α1,α2,α3\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \boldsymbol{\alpha}_3 线性表出等价于判断线性方程组

x1α1+x2α2+x3α3=βx_1 \boldsymbol{\alpha}_1+x_2 \boldsymbol{\alpha}_2+x_3 \boldsymbol{\alpha}_3=\boldsymbol{\beta}

是否有解. 因此, 作如下的初等变换:

(15122−5−3−1−31263)⟶(15120−15−5−502799)⟶(151203110000),\left(\begin{array}{ccc|c} 1 & 5 & 1 & 2 \\ 2 & -5 & -3 & -1 \\ -3 & 12 & 6 & 3 \end{array}\right) \longrightarrow\left(\begin{array}{ccc|c} 1 & 5 & 1 & 2 \\ 0 & -15 & -5 & -5 \\ 0 & 27 & 9 & 9 \end{array}\right) \longrightarrow\left(\begin{array}{lll|l} 1 & 5 & 1 & 2 \\ 0 & 3 & 1 & 1 \\ 0 & 0 & 0 & 0 \end{array}\right),

由此可以看出, 这个线性方程组有解. 因此 β\boldsymbol{\beta} 能够由向量组 α1,α2,α3\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \boldsymbol{\alpha}_3 线性表出. 把阶梯形矩阵进一步简化:

(151203110000)⟶(10−23130113130000),\left(\begin{array}{llll} 1 & 5 & 1 & 2 \\ 0 & 3 & 1 & 1 \\ 0 & 0 & 0 & 0 \end{array}\right) \longrightarrow\left(\begin{array}{cccc} 1 & 0 & -\frac{2}{3} & \frac{1}{3} \\ 0 & 1 & \frac{1}{3} & \frac{1}{3} \\ 0 & 0 & 0 & 0 \end{array}\right),

于是

{x1=23x3+13x2=−13x3+13\left\{\begin{array}{l} x_1=\frac{2}{3} x_3+\frac{1}{3} \\ x_2=-\frac{1}{3} x_3+\frac{1}{3} \end{array}\right.

其中 x3x_3 是自由未知量, 方程组有无穷多个解, 因此 β\boldsymbol{\beta} 由向量组 α1,α2,α3\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \boldsymbol{\alpha}_3 线性表出的方式有无穷多种. 为了写出一种表出方式, 令 x3=1x_3=1, 得到 x1=1,x2=0x_1=1, x_2=0, 于是有 β=\boldsymbol{\beta}= α1+α3\boldsymbol{\alpha}_1+\boldsymbol{\alpha}_3.

由例 2 知道, 判断三元非齐次线性方程组是否有解可以考察 b\boldsymbol{b} 是不是向量组 α1,α2\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, α3\boldsymbol{\alpha}_3 的某一个线性组合, 为此, 我们把向量组 α1,α2,α3\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \boldsymbol{\alpha}_3 的所有线性组合组成一个集合 WW, 即 W={k1α1+k2α2+k3α3∣ki∈R,i=1,2,3}W=\left\{k_1 \boldsymbol{\alpha}_1+k_2 \boldsymbol{\alpha}_2+k_3 \boldsymbol{\alpha}_3 \mid k_i \in \mathbf{R}, i=1,2,3\right\}.

非齐次线性方程组的解的性质

对于非齐次线性方程组的解可以得到下面的性质.

性质 1 若 η1,η2\boldsymbol{\eta}_1, \boldsymbol{\eta}_2 都是非齐次线性方程组 Ax=b\boldsymbol{A} \boldsymbol{x}=\boldsymbol{b} 的解, 则 η1−η2\boldsymbol{\eta}_1-\boldsymbol{\eta}_2 是对应齐次线性方程组 Ax=0\boldsymbol{A x}=\mathbf{0} 的解.

性质 2 若 η\boldsymbol{\eta} 是 Ax=b\boldsymbol{A x}=\boldsymbol{b} 的一个解, ξ\boldsymbol{\xi} 是 Ax=0\boldsymbol{A x}=\mathbf{0} 的一个解, 则 η+ξ\boldsymbol{\eta}+\boldsymbol{\xi} 是 Ax=b\boldsymbol{A x}=\boldsymbol{b} 的一个解.

定理 1 设 η∗\boldsymbol{\eta}^* 为非齐次线性方程组 Ax=b\boldsymbol{A} \boldsymbol{x}=\boldsymbol{b} 的一个特解, 则这个非齐次线性方程组的任一解 xx 可以表示为

x=η∗+k1ξ1+k2ξ2+⋯+ksξs\boldsymbol{x}=\boldsymbol{\eta}^*+k_1 \boldsymbol{\xi}_1+k_2 \boldsymbol{\xi}_2+\cdots+k_s \boldsymbol{\xi}_s

的形式, 其中 ξ1,ξ2,⋯ ,ξ\boldsymbol{\xi}_1, \boldsymbol{\xi}_2, \cdots, \boldsymbol{\xi} 是对应齐次线性方程 Ax=0\boldsymbol{A} \boldsymbol{x}=\mathbf{0} 的基础解系, k1,k2,⋯ ,ksk_1, k_2, \cdots, k_s是任意常数.

证明: 由性质 2 可以知道, x=η∗+k1ξ1+k2ξ2+⋯+ksξs\boldsymbol{x}=\boldsymbol{\eta}^*+k_1 \boldsymbol{\xi}_1+k_2 \boldsymbol{\xi}_2+\cdots+k_s \boldsymbol{\xi}_s 是 Ax=b\boldsymbol{A} \boldsymbol{x}=\boldsymbol{b} 的解. 反之, 对 Ax=b\boldsymbol{A x}=\boldsymbol{b} 的任意一个解 x\boldsymbol{x}, 由性质 1 可以知道 x−η∗\boldsymbol{x}-\boldsymbol{\eta}^* 是 Ax=0\boldsymbol{A} \boldsymbol{x}=\mathbf{0} 的解, 根据基础解系的定义,必然存在常数 k1,k2,⋯ ,ksk_1, k_2, \cdots, k_s 使得解向量 x−η∗=k1ξ1+k2ξ2+⋯+ksξs\boldsymbol{x}-\boldsymbol{\eta}^*=k_1 \boldsymbol{\xi}_1+k_2 \boldsymbol{\xi}_2+\cdots+k_s \boldsymbol{\xi}_s, 于是可以得到 x=η∗+k1ξ1+k2ξ2+⋯+ksξs\boldsymbol{x}=\boldsymbol{\eta}^*+k_1 \xi_1+k_2 \boldsymbol{\xi}_2+\cdots+k_s \xi_s.

这样, 可以把 x=η∗+k1ξ1+k2ξ2+⋯+ksξs \boldsymbol{x}=\boldsymbol{\eta}^*+k_1 \boldsymbol{\xi}_1+k_2 \boldsymbol{\xi}_2+\cdots+k_s \boldsymbol{\xi}_{\text {s }} 称为方程组 Ax=b\boldsymbol{A} \boldsymbol{x}=\boldsymbol{b} 的通解.

比如, 对例 1 的非齐次线性方程组, 取一个特解为 (1,1,0)T(1,1,0)^{\mathrm{T}}; 进一步, 对齐次线性方程组的系数矩阵作行初等变换可以得到

(1420211−2−1)→(100021000),\left(\begin{array}{ccc} 1 & 4 & 2 \\ 0 & 2 & 1 \\ 1 & -2 & -1 \end{array}\right) \rightarrow\left(\begin{array}{lll} 1 & 0 & 0 \\ 0 & 2 & 1 \\ 0 & 0 & 0 \end{array}\right),

于是得到方程组

{x1=0,2x2+x3=0,\left\{\begin{array}{l} x_1=0, \\ 2 x_2+x_3=0, \end{array}\right.

因此齐次线性方程组的一个基础解系为 (0,1,−2)T(0,1,-2)^{\mathrm{T}}. 由定理 1, 这个非齐次线性方程组的通解为

x=(110)+k(01−2),\boldsymbol{x}=\left(\begin{array}{l} 1 \\ 1 \\ 0 \end{array}\right)+k\left(\begin{array}{c} 0 \\ 1 \\ -2 \end{array}\right),

其中 kk 可以取任意常数.

例设空间中三个平面的方程构成的方程组为

{x1+ax2+x3=1,−x1+x2+ax3=−1,x1+x2+x3=1.\left\{\begin{array}{c} x_1+a x_2+x_3=1, \\ -x_1+x_2+a x_3=-1, \\ x_1+x_2+x_3=1 . \end{array}\right.

（1）当三个平面相交于一点时, 其中的 aa 为何值? 求交点的坐标. （2）当三个平面相交于同一直线时，其中的 aa 为何值? 解：对三个平面的方程构成的线性方程组的增广矩阵进行行初等变换

(1a11−11a−11111)→r1+r2−r1+r3(1a110a+1a+1001−a00)→r3+r2\left(\begin{array}{ccc|c} 1 & a & 1 & 1 \\ -1 & 1 & a & -1 \\ 1 & 1 & 1 & 1 \end{array}\right) \xrightarrow{\substack{r_1+r_2 \\ -r_1+r_3}}\left(\begin{array}{ccc|c} 1 & a & 1 & 1 \\ 0 & a+1 & a+1 & 0 \\ 0 & 1-a & 0 & 0 \end{array}\right) \xrightarrow{r_3+r_2}
(1a1102a+1001−a00)→12(a−1)r2+r3(1a1102a+100012(a2−1)0).\left(\begin{array}{ccc|c} 1 & a & 1 & 1 \\ 0 & 2 & a+1 & 0 \\ 0 & 1-a & 0 & 0 \end{array}\right) \xrightarrow{\frac{1}{2}(a-1) r_2+r_3}\left(\begin{array}{ccc|c} 1 & a & 1 & 1 \\ 0 & 2 & a+1 & 0 \\ 0 & 0 & \frac{1}{2}\left(a^2-1\right) & 0 \end{array}\right) .

（1）如果三个平面相交于一点, 即线性方程组有唯一解, 那么 12(a2−1)≠0\frac{1}{2}\left(a^2-1\right) \neq 0, 即 a≠a \neq ±1\pm 1. 当 a≠±1a \neq \pm 1 时, 继续对增广矩阵作行初等变换:

(1a1102a+100012(a2−1)0)→(100101000010),\left(\begin{array}{ccc|c} 1 & a & 1 & 1 \\ 0 & 2 & a+1 & 0 \\ 0 & 0 & \frac{1}{2}\left(a^2-1\right) & 0 \end{array}\right) \rightarrow\left(\begin{array}{ccc|c} 1 & 0 & 0 & 1 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{array}\right),

所以 x1=1,x2=0,x3=0x_1=1, x_2=0, x_3=0. 这三个平面相交于点 (1,0,0)(1,0,0). (2) 如果三个平面相交于同一直线, 即线性方程组有无穷多个解, 同时三个平面不能重合, 那么 a=±1a= \pm 1. 当 a=1a=1 时, 增广矩阵经过行初等变换得到

(111102200000)→(100101100000),\left(\begin{array}{lll|l} 1 & 1 & 1 & 1 \\ 0 & 2 & 2 & 0 \\ 0 & 0 & 0 & 0 \end{array}\right) \rightarrow\left(\begin{array}{lll|l} 1 & 0 & 0 & 1 \\ 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 0 \end{array}\right),

所以 x1=1,x2=−x3x_1=1, x_2=-x_3, 则这个线性方程组的通解为

(x1x2x3)=(11−1)+k(01−1)\left(\begin{array}{l} x_1 \\ x_2 \\ x_3 \end{array}\right)=\left(\begin{array}{c} 1 \\ 1 \\ -1 \end{array}\right)+k\left(\begin{array}{c} 0 \\ 1 \\ -1 \end{array}\right)

其中 kk 为任意常数. 这时, 三个平面相交于过点 (1,1,−1)(1,1,-1), 以 (0,1,−1)(0,1,-1) 为方向向量的直线. 当 a=−1a=-1 时, 增广矩阵经过行初等变换得到

(1−11102000000)→(101101000000),\left(\begin{array}{ccc|c} 1 & -1 & 1 & 1 \\ 0 & 2 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array}\right) \rightarrow\left(\begin{array}{lll|l} 1 & 0 & 1 & 1 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array}\right),

所以 x1+x3=1,x2=0x_1+x_3=1, x_2=0, 则这个线性方程组的通解为

(x1x2x3)=(001)+k(10−1)\left(\begin{array}{l} x_1 \\ x_2 \\ x_3 \end{array}\right)=\left(\begin{array}{l} 0 \\ 0 \\ 1 \end{array}\right)+k\left(\begin{array}{c} 1 \\ 0 \\ -1 \end{array}\right)

其中 kk 为任意常数. 这时, 三个平面相交于过点 (0,0,1)(0,0,1), 以 (1,0,−1)(1,0,-1) 为方向向量的直线.

Previous7._齐次方程组解的性质
Next9._非齐次线性方程组解的结构_基础解系