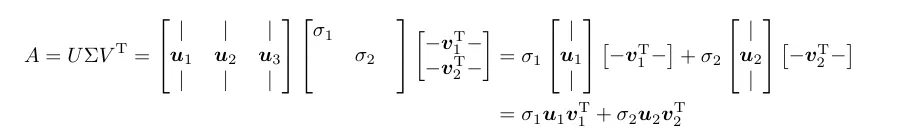矩阵的五种分解
为了处理矩阵,人们把矩阵进行了分解,主要包括五种分解:
(1) A=CR
(2) A=LU
(3) A=QR
(4) A=QΛQT
(5) A=U∑VT
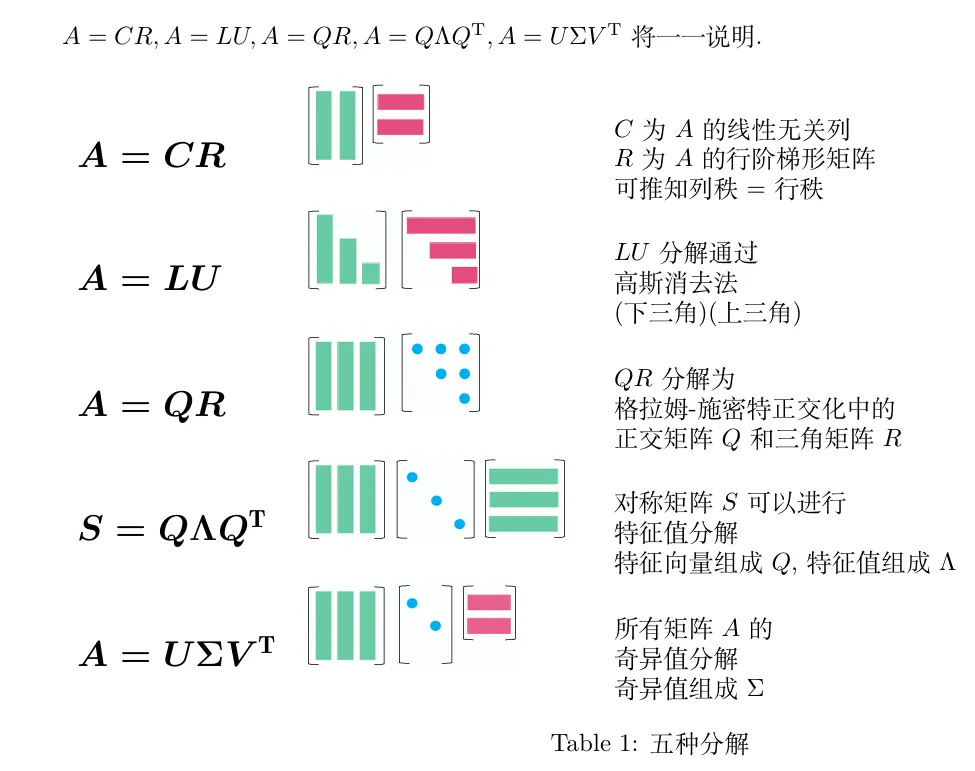
A=CR
A=CR 所有一般的长矩阵 A 都有相同的行秩和列秩.这个分解是理解这一定理最直观的方法.C 由 A 的线性无关列组成,R 为 A 的行阶梯形矩阵(消除了零行).A=CR 将 A 化简为 r 的线性无关列 C 和线性无关行 R的乘积.
A[122335]=CR=[1223][100111] 推导过程:从左往右看 A 的列。保留其中线性无关的列,去掉可以由前者线性表出的列。则第1、2列被保留,而第三列因为可以由前两列之和表示而被去掉。而要通过线性无关的 1、2 两列重新构造出 A ,需要右乘一个行阶梯矩阵 R .
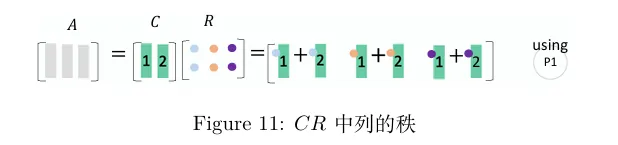
现在你会发现行的秩为 2 ,因为 C 中只有 2 个线性无关列.而 A 中所有的列都可以由 C 中的 2 列线性表出.
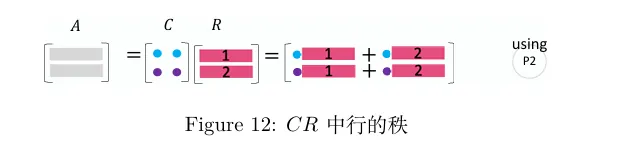
A=LU
用高斯消除法求解 Ax=b 也被称为 LU 分解。通常,是 A 左乘一个初等行变换矩阵 (E) 来得到一个上三角矩阵 U 。
EAA let L=E−1,A=U=E−1U=LU 现在,求解 Ax=b 有2步:(1)求解 Lc=b ,(2)代回 Ux=c .
在这里,我们直接通过 A 计算 L 和 U .
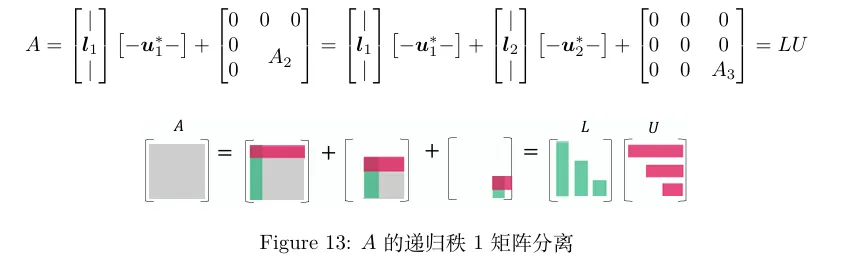
要计算 L 和 U ,首先分离出由 A 的第一行和第一列组成的外积.余下的部分为 A2 .递归执行此操作,将 A 分解为秩1矩阵之和.
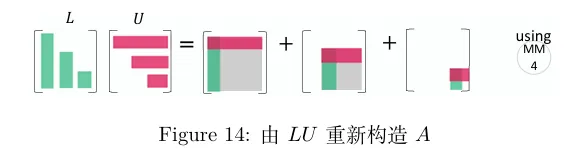
由 L 乘以 U 来重新构造 A 则相对简单。
A=QR
A=QR 是在保持 C(A)=C(Q) 的条件下,将 A 转化为正交矩阵 Q .
在格拉姆-施密特正交化中,首先,单位化的 a1 被用作 q1 ,然后求出 a2 与 q1 正交所得到的 q2 ,以此类推.
q1=a1/∥a1∥q2=a2−(q1Ta2)q1,q2=q2/∥q2∥q3=a3−(q1Ta3)q1−(q2Ta3)q2,q3=q3/∥q3∥ 或者你也可以写作 rij=qiTaj :
a1=r11q1a2=r12q1+r22q2a3=r13q1+r23q2+r33q3 原本的 A 就可以表示为 QR :正交矩阵乘以上三角矩阵.
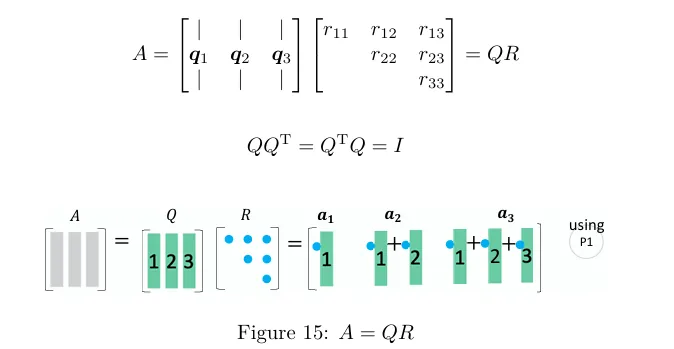
A 的列向量就可以转化为一个正交集合:Q 的列向量.A 的每一个列向量都可以用 Q 和上三角矩阵 R 重新构造出.
图释可以回头看 P1.
S=QΛQT
所有对称矩阵 S 都必须有实特征值和正交特征向量.特征值是 Λ 的对角元素,特征向量在 Q 中.
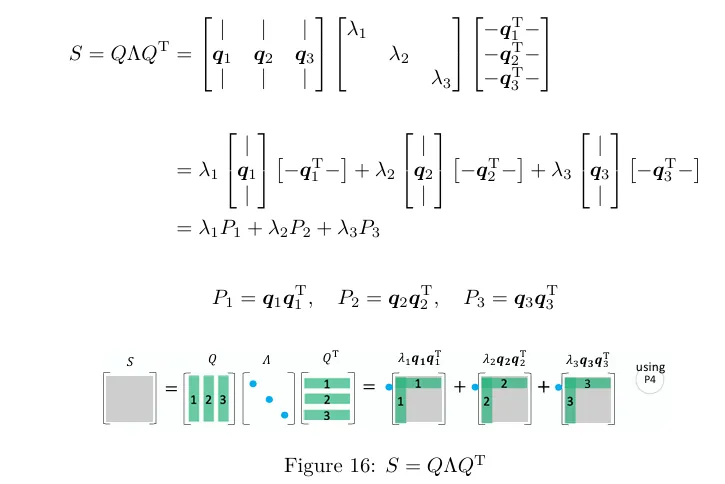
一个对称矩阵 S 通过一个正交矩阵 Q 和它的转置矩阵,对角化为 Λ 。然后被分解为一阶投影矩阵 P=qqT的组合.这就是谱定理.
S=ST=λ1P1+λ2P2+λ3P3QQT=P1+P2+P3=IP1P2=P2P3=P3P1=OP12=P1=P1T,P22=P2=P2T,P32=P3=P3T A=UΣVT
包括长方阵在内的所有矩阵都具有奇异值分解(SVD).A=UΣVT 中,有 A 的奇异向量 U 和 V 。奇异值则排列在 Σ 的对角线上.下图就是"简化版"的 SVD.
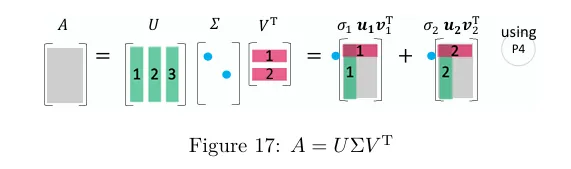 你可以发现,V 是 Rn( ATA 的特征向量)的标准正交基,而 U 是 Rm( AAT 的特征向量)的标准正交基.它们共同将 A 对角化为 Σ .这也可以表示为秩 1 矩阵的线性组合.
你可以发现,V 是 Rn( ATA 的特征向量)的标准正交基,而 U 是 Rm( AAT 的特征向量)的标准正交基.它们共同将 A 对角化为 Σ .这也可以表示为秩 1 矩阵的线性组合.
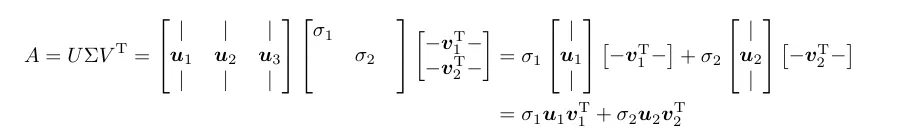
注意:
UUTVVT=Im=In 






 你可以发现, 是 ( 的特征向量)的标准正交基,而 是 ( 的特征向量)的标准正交基.它们共同将 对角化为 .这也可以表示为秩 1 矩阵的线性组合.
你可以发现, 是 ( 的特征向量)的标准正交基,而 是 ( 的特征向量)的标准正交基.它们共同将 对角化为 .这也可以表示为秩 1 矩阵的线性组合.