物体的参照物
在高中,都学习过物体的参照物,我们常说“地球绕着太阳转”,其实默认了太阳是静止的,而地球是运动的,同样这个运动,如果我们以地球为参照物,也可以说是太阳绕着地球转,但是可以发现,两者方向正好相反。所以,旋转参照物不同,所得的结果并不一定相同,这个参照物,就是数学中说的基,而物体的速度类似物体的坐标。
关于过度矩阵更详细介绍请参考 坐标变换
坐标轴平移
不改变坐标轴的方向和长度单位,只变换原点的位置,这种坐标系的变换叫做坐标轴的平移,简称移轴.
给定一坐标系OXY, 平移坐标轴得到新坐标系O′X′Y′, 下面我们来确定平面上任意一点P的新坐标(x′,y′)与原坐标(x,y)之间的关系(图6.27).
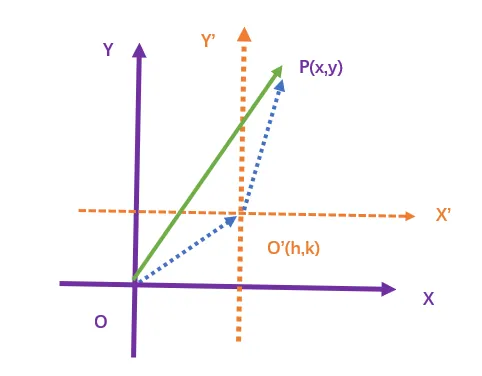
设O′在坐标系OXY中的坐标为(h,k), 则在坐标系OXY中
OO′=(h,k),OP=(x,y),O′P=(x′,y′)因为OP=OO′+O′P,所以 (x,y)=(h,k)+(x′,y′)
即:
x=x′+h,y=y′+k
或
x′=x−h,y′=y−k
公式(6.19), (6.20)叫做平移公式或移轴公式.
例平移坐标轴,化简圆的方程x2+y2+2x−6y+6=0
解: 把已知圆的方程配方得 (x+1)2+(y−3)2=4 设它上面任一点的新坐标为
(x′,y′), 平移坐标轴使
x′=x+1,y′=y−3
即:x=x′−1,y=y′+3,代入(6.21),得到新方程为(图6.28)
x′2+y′2=4
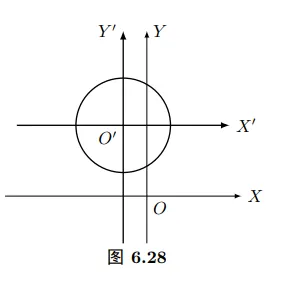
从例6.15可以看出,适当地变换坐标系,可以使曲线的方程简化.由于曲线的几何性质与我们选取的坐标系无关.所以,我们研究曲线时,总是想法选择能使曲线方程最为简单的坐标系,以便于我们研究曲线的性质.
坐标轴的旋转
不改变坐标轴的原点和长度单位,只是坐标轴绕原点转一角度,这种坐标系的变换叫做坐标轴的旋转,简称转轴.
给定一坐标系,坐标轴绕原点O转θ角,得到一新坐标
系OX′Y′(图6.29). 下面我们来确定平面上任一点P的新坐标(x′,y′)与原坐标(x,y)之间的关系.
设ex,ey和ex′,ey′分别是两个坐标系中的基向
量,则
OPex′ey′=xex+yey=x′ex′+y′ey′=cosθex+sinθey=cos(2π+θ)ex+sin(2π+θ)ey=−sinθex+cosθey 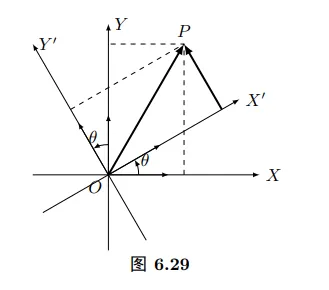 代入上式,得
xeX+yeY=(x′cosθ−y′sinθ)eX+(x′sinθ+y′cosθ)eY
所以:
代入上式,得
xeX+yeY=(x′cosθ−y′sinθ)eX+(x′sinθ+y′cosθ)eY
所以:
{x=x′cosθ−y′sinθy=x′sinθ+y′cosθ...(6.22) 由(6.22)解出x′,y′得
{x′=xcosθ+ysinθy′=−xsinθ+ycosθ...(6.23) (6.22)式是用新坐标来表示原坐标的公式,(6.23)式是用原坐标来表示新坐标的公式,它们统称为{旋转公式或转轴公式.
一般的坐标变换公式
设OXY, O′X′Y′是两个坐标系(图6.31),O′在坐标系OXY中的坐标是(h,k), 容易看出,把坐标系OXY作移轴变换,把原点O移到O′(h,k)得到坐标系O′XY然后再绕O′旋转θ角就可得到坐标系
O′X′Y′, 这就说,上述的一般的坐标变换是平移与旋转的合成.下面我们来确定,平面上任意一点P的新坐标(x′,y′)与原坐标(x,y)之间的关系.
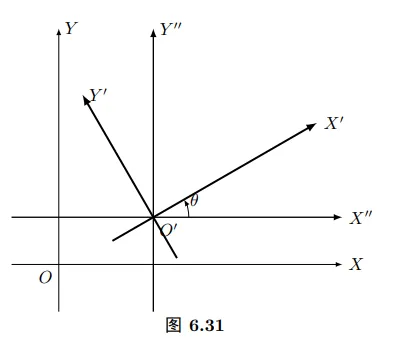
设 OXY 经过移轴后得到的坐标系为O′XY
(图6.31),则由平移公式,得
{x=x′′+hy=y′′+k 再由旋转公式,得
{x′′=x′cosθ−y′sinθy′′=x′sinθ+y′cosθ 把(6.25)代入(6.24),得
{x=x′cosθ−y′sinθ+hy=x′sinθ+y′cosθ+k 由(6.26)式解出x′,y′又可得
{x′=(x−h)cosθ+(y−k)sinθy′=−(x−h)sinθ+(y−k)cosθ (6.26), (6.27)两个公式就是一般的坐标变换公式.公式(6.26)是
通过新坐标来表示原坐标,公式(6.27)是通过原坐标来表示新
坐标.
坐标与坐标系的选择
准确描述:坐标系的变换与点的坐标变换互为逆变换.还有个原点对应平移变换.
1)点的坐标变换:点 P 在 A 系统坐标 (x,y,z)A ,而到 B 系统后,它的新坐标 (x′,y′,z′)B ,即 (x,y,z)A→(x′,y′,z′)B ;
2)坐标系变换(原点变换+坐标轴变换/基变换):O→O′;e1,e2,e3→e1′,e2′,e3′ .
其中,A坐标系统 A[O;e1,e2,e3], O(0,0,0)A,e1,e2,e3 分别是 x,y,z 轴单位向量;
B 坐标系统 B[O′;e1′,e2′,e3′],O′(0,0,0)B=O′(x0,y0,z0)A,e1′,e2′,e3′ 分别是 x′,y′,z′轴单位向量;
注:(x,y)A 指A系统下坐标,(x,y)B 指B系统下坐标.
原点变换,本质是平移变换,即 O→O′ ;
基变换,本质是向量变换,也是旋转变换 ,让 A 系统坐标轴旋转到与 B 系统坐标轴平行.
也就是说,直角坐标系变换是基变换(先旋转)与原点变换(后平移)的复合变换.
当一个向量在一个坐标系下表示的坐标为A,在另外一个坐标系下表示的是B,那么由A到B的转换,可以通过乘以一个矩阵实现,这个矩阵就是过渡矩阵。
设 α1,α2,⋯,αn 与 β1,β2,⋯,βn 是 n 维向量空间 V 的两个基,存在系数矩阵 Pn×n ,使得
(β1,β2,⋯,βn)=(α1,α2,⋯,αn)P, 矩阵 Pn×n 称为从基 α1,α2,⋯,αn 到基 β1,β2,⋯,βn 的过渡矩阵.
显然,从基 α1,α2,⋯,αn 到基 β1,β2,⋯,βn 的过渡矩阵 Pn×n 是可逆矩阵.
关于过渡矩阵的介绍,请参考 过渡矩阵视频


 代入上式,得
所以:
代入上式,得
所以: