对角线矩阵
若一个方阵除了主对角线上的元素外其余元素都等于零, 就称之为对角阵. 对角阵的形状为
Λ=a110⋮00a22⋮0⋯⋯⋯00⋮ann 上述对角阵可简记为 diag{a11,a22,⋯,ann}.
单位矩阵
若进一步有 a11=a22=⋯=ann=1, 则称这个矩阵为单位阵. n 阶单位阵通常记为 In 或者En 表示。
行矩阵和列矩阵
按照分开矩阵的做法,如果把矩阵按行或者列进行划分,就可以得到行分块矩阵和列分块矩阵。
对角形矩阵的逆
容易知道他的逆为
Λ−1=A1−1A2−1⋱As−1 例 设矩阵 A=12000−10000100002 ,求 A−1 .
解:将 A 分块成分块对角阵 A=(A1OOA2) ,其中 A1=(120−1),A2=(1002).
有 A1−1=(120−1),A2−1=(10021) ,所以
A−1=(A1−1A2−1)=12000−100001000021. 矩阵乘以对角矩阵
这里特别强调一下矩阵乘以对角线矩阵
矩阵乘以对象形矩阵相当于直接对矩阵的各列按照对角线上的数字缩放。
右乘对角矩阵
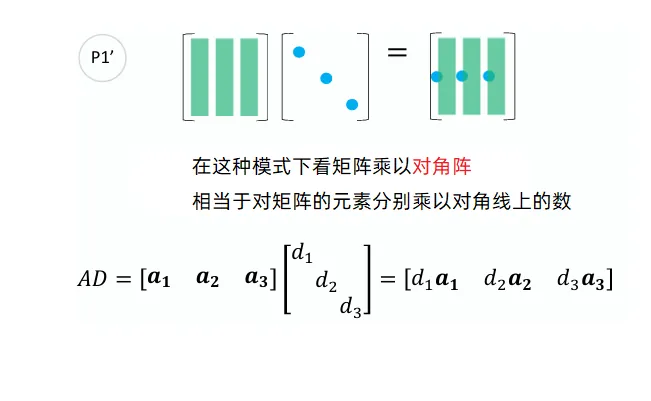
左乘对角矩阵
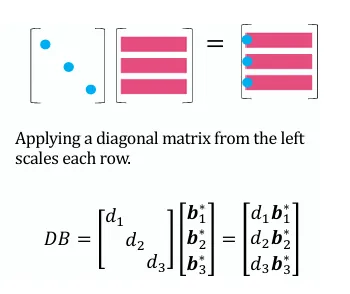
中间乘对角矩阵
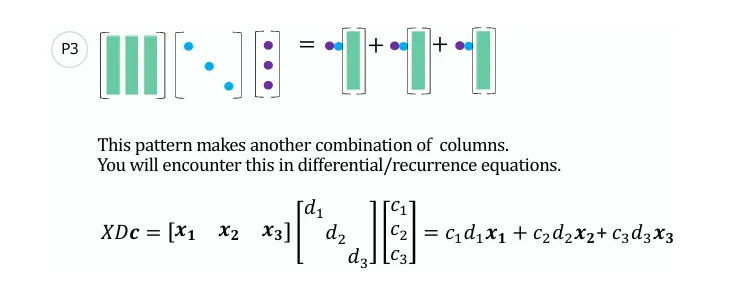
标准形矩阵
形如
D=1⋱10⋱0 得m×n矩阵称为标准形矩阵
如果一个矩阵满足:
①左上角是一个单位矩阵;
②其他元全为0;
在阶梯形矩阵里介绍了行最简简形矩阵。
对于行最简形矩阵再实施初等列变换,可变成一种形状更简单的矩阵. 例如, 将上面的行最简形矩阵再实施初等列变换
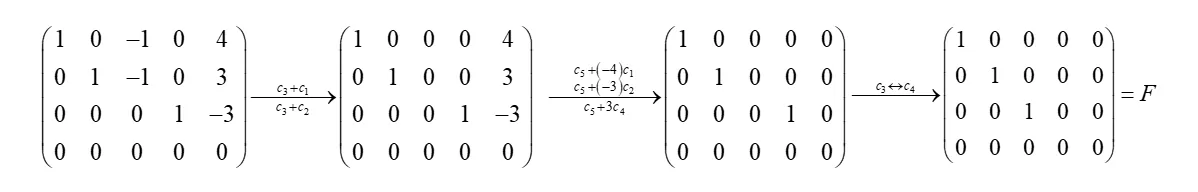 最后一个矩阵称为矩阵的标准形,写成分块矩阵的形式,则有 F=(E3ooo)
对于一般的矩阵,我们有下面的结论:
01任意一个 m×n 矩阵总可以经过若干次初等行变换化为行阶梯形矩阵;
02 任意一个 m×n 矩阵总可以经过若干次初等行变换化为行最简形矩阵;
03 任意一个 m×n 矩阵总可以经过若干次初等变换化为它标准形 F=(Er0o0)m,n,
04 其中 r 为行阶梯形矩阵中非零行的行数.
最后一个矩阵称为矩阵的标准形,写成分块矩阵的形式,则有 F=(E3ooo)
对于一般的矩阵,我们有下面的结论:
01任意一个 m×n 矩阵总可以经过若干次初等行变换化为行阶梯形矩阵;
02 任意一个 m×n 矩阵总可以经过若干次初等行变换化为行最简形矩阵;
03 任意一个 m×n 矩阵总可以经过若干次初等变换化为它标准形 F=(Er0o0)m,n,
04 其中 r 为行阶梯形矩阵中非零行的行数.
标准形的作用
前面说过,线性方程组可以写成矩阵,反过来也一样,使用矩阵也可以写出线性方程组。
在标准型里,如果写成方程的形式就是:
⎩⎨⎧x+0+⋯+0=b1,0+x2+⋯+0=b2,⋯⋯⋯0+0+⋯+xn=bm, 也就是从标准型,可以立刻写出方阵组的解。
http://kb.kmath.cn/kbase/detail.aspx?id=461



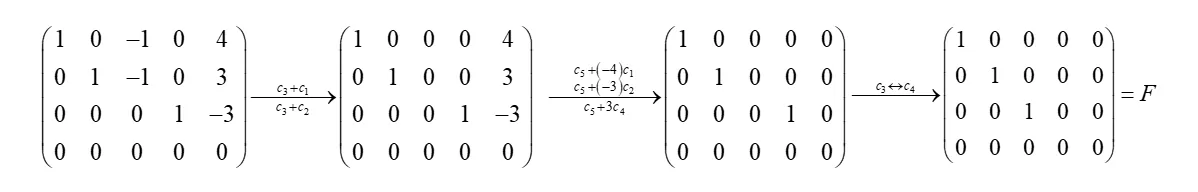 最后一个矩阵称为矩阵的标准形,写成分块矩阵的形式,则有
对于一般的矩阵,我们有下面的结论:
01任意一个 矩阵总可以经过若干次初等行变换化为行阶梯形矩阵;
02 任意一个 矩阵总可以经过若干次初等行变换化为行最简形矩阵;
03 任意一个 矩阵总可以经过若干次初等变换化为它标准形 ,
04 其中 为行阶梯形矩阵中非零行的行数.
最后一个矩阵称为矩阵的标准形,写成分块矩阵的形式,则有
对于一般的矩阵,我们有下面的结论:
01任意一个 矩阵总可以经过若干次初等行变换化为行阶梯形矩阵;
02 任意一个 矩阵总可以经过若干次初等行变换化为行最简形矩阵;
03 任意一个 矩阵总可以经过若干次初等变换化为它标准形 ,
04 其中 为行阶梯形矩阵中非零行的行数.