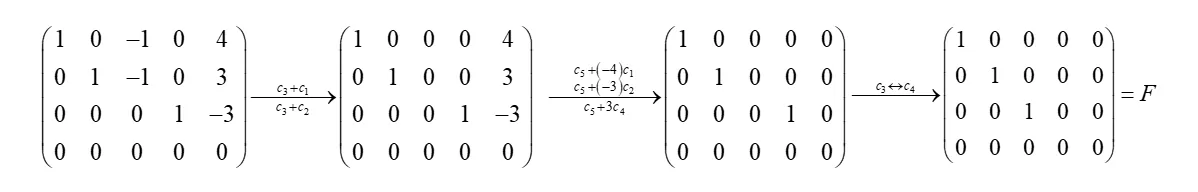阶梯形矩阵在整个矩阵系统里占据极其重要的位置,很多题目都涉及利用矩阵的初等变换化为阶梯形矩阵,因此务必掌握。
为何引入阶梯形矩阵
回顾矩阵的初等变换,矩阵的初等变换共有三条规则:
①交换矩阵的某两行;
②矩阵的某一行乘以非零数;
③将矩阵的某一行的k倍加到另一行
利用这三条规则,可以化简矩阵为阶梯形矩阵。
为什么要化为阶梯形矩阵?因为通过阶梯形矩阵可以获取矩阵很多的性质,比如矩阵的秩,方程组的解等。请看一个方程组。
⎩⎨⎧x1+2x2+x33x1−x2−3x32x1+3x2+x3=3=−1=4 上面这个方程最终可化为下面的方程组:
⎩⎨⎧x1+2x2+−7x2−x3=36x3=−10−x3=−4 利用回代法,从第三个方程开始,由下往上,即可顺利得到方程组的解。因此,在“效率”和“功能”方面,当一个方程化成类似上面的形式时,就能满足我们90%的任务了。如果继续化简,还可以换成行最简型。
因此,这里就引入阶梯形矩阵。
阶梯行矩阵
在上例中,线性方程组对应的增广矩阵有一个共同特点,就是: 可画一条阶梯线,线的下方全为零;每个台阶只有一行,台阶数就是非零行的行数;每一非零行的第一个非零元素位于上一行首元的右侧,
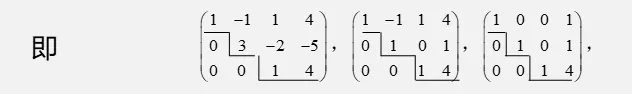
这样的矩阵,我们称为行阶梯形矩阵.
即判断是否是阶梯形矩阵,主要在于2点:
(1) 若有零行,则零行都在矩阵的最下方;
(2) 首非零元(非零行的第一个不为零的元素)的列标随着行标的递增而严格增大.
在实际判断里,都是通过想象画下进行判断,如下图两个都是阶梯形矩阵。
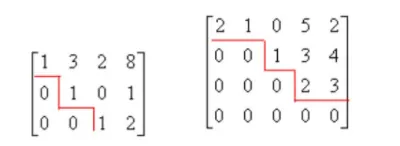
注意 阶梯形矩阵,每次只能下降1个台阶,但是允许跨多列
如下图,第一个矩阵一下子下降2个阶梯,这种不是阶梯形矩阵。

行最简形矩阵
下面这个矩阵就是行最简形矩阵。
 {width=400px}
{width=400px}
最简形矩阵最大的好处是,如果直接把x1,x2...xn 带入,即可直接得到方程组的解。
定义:对于一个矩阵,如果他是阶梯形矩阵,且它的非零行的第一个非零元素全为 1 ,并且这些非零元素所在的列的其余元素全为零, 这样的矩阵,我们称为行最简形矩阵.
下图显示的是两个行最简形矩阵。
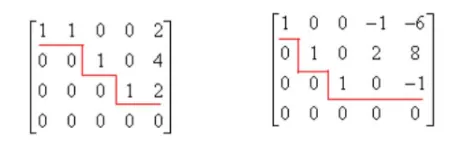
再如下图,第3行都是零,再最下面,首行非零元都是1,而且又是阶梯形,因此他是行最简形矩阵
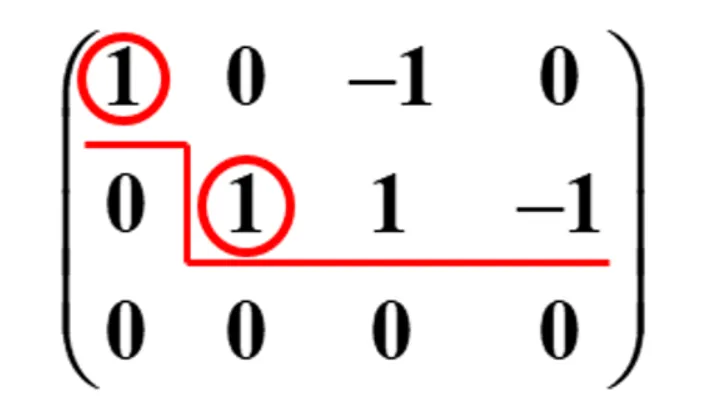 {width=200px}
{width=200px}
再次强调一下行最简形矩阵的条件
(1)非零行的首非零元为1
(2)首非零元所在列的其它元素都是零。
矩阵的阶梯形矩阵不是唯一的,但是行最简形矩阵是唯一的。
阶梯形矩阵的化法
例试用矩阵的初等行变换将矩阵 A=221−1−3−1141−1−2−3−11122242 先化为阶梯形矩阵.
解:第一步:交换第一行和第三行的位置,想一想,为什么要交换第一行和第三行?因为第3行第一个元素是1,我们使用他来最为基础行,然后消去后面的行会计算比较方便。
A=221−1−3−1141−1−2−3−11122242⟶r1↔r3122−11−1−34−2−11−311−124222 第二步 第一行保持不变,然后用第一行消去第二行、第一行消去第三行、第一行消去第四行。即
①第一行的-2倍加到第二行
②第一行的-2倍加到第三行
③第一行的1倍加到第四行
A⟶(−2r1)+r2(−2r1)+r3r1+r410001−3−55−235−51−1−334−6−66 现在第一列已经处理完毕(第1列主对角线下方都是0),后续第一列不再主动参与后面的变换(被动可以),可以想象一下,只要第一行主动加到下面的行,就会把已经化简的0,又变成非0。但是从下往上加是可以的。
第三步 下面开始处理第2列。我们注意到第3行和第4互为相反数,所以,先把第3行加到第4行。
A⟶r3+r410001−3−50−23501−1−304−6−60 现在第2行乘以−35 然后加到第3行
A⟶r2∗(−35)+r310001−300−23001−1−3404−640 此时,第3行出现了分数,已经不方便计算,因此,第三行乘以3,消去分数
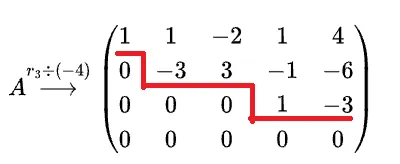
A⟶r3∗510001−300−23001−1−404−6120 把第3行公约数-4提取出来
A⟶r3÷(−4)10001−300−23001−1104−6−30 现在第2列已经处理完毕(第2列主对角线下方都是0),开始处理第3列。观察到第3列下方已经是0,此时就如果画出折现,就可以发现他已经是阶梯形矩阵了。
行最简形矩阵
我们继续上一题,在已经是阶梯形矩阵的情况下,把他化为行最简形矩阵。
例在上图里,第一列已经满足行最简形矩阵,但是第2列不满足,为此需要把第2行第2列的元素变为1 因此第二行乘以−31
A⟶r2∗(−31)10001100−2−1001311042−30 行最简形要求第二列的第一行为零,但是现在为1, 因此用第2行的-1倍,加上第一行上去。 (注意:此时只能从下往上加。因为,从上往下,一旦第一行-1倍加到下面的第2行上去,那么前面已经化好的数据就又变成非0)
A⟶−r2+r110000100−1−10032311022−30 现在处理第4列, 把第3行乘以−32 加到第一行,把第3行乘以−31 加到第二行
A⟶10000100−1−100001043−30 上述就是行最简形矩阵。
例计算矩阵的秩
A=2354−3−24643−3−4542−5 解: 因为现 在a11=2 ,若将 a21,a31 化零时会出现分数。 我们要尽可能想办法让行列式中a11=1,(当然-1也可以) , 一种方法是第一行提取公因子法,即第一行提取一个公因子2,但是这样后面几个数字也会出现分数。
为此,先将 D 中第二 行的 −1 倍加到第一行上,使新的 a11=−1 .根据新的第 1 行的特点,将 a12,a13,a14 化为零更方便,
① 将第2行的-1倍加到第一行上,结果如下。
A=−1354−1−24613−3−4142−5 去掉负号
A=13541−246−13−3−4−142−5 然后
(i)第一行乘以-3 加到第二行
(i)第一行乘以-5 加到第三行
(i)第一行乘以-4 加到第四行
A=10001−5−12−1620−177−1 交换第2,3行位置
A=10001−1−52−1260−177−1 ①第二行的1倍加到第一行
②第二行的-5倍加到第三行
②第二行的2倍加到第四行
A=10000−10012−4467−2813 现在把第三行提取 -4 (目的是让他变成1),得
A=10000−100121467713 ① 第三行乘以-1加到第一行
②第三行乘以-2加到第二行
③第三行乘以-4加到第四行
A=10000−1000010−1−77−15 矩阵初等变换有一个性质:将某行全体元素都乘以某一非零常数。 这里 -15 看起来很碍眼,所以第四行直接提取 -15倍(相当于把-15变成1)
第二行直接提取-1
第四行直接提出-15
A=100001000010−1771 用第四行消去上面3行,最终结果为
1000010000100001 矩阵的标准形
对于行最简形矩阵再实施初等列变换,可变成一种形状更简单的矩阵. 例如下面有一个矩阵可以简化如下
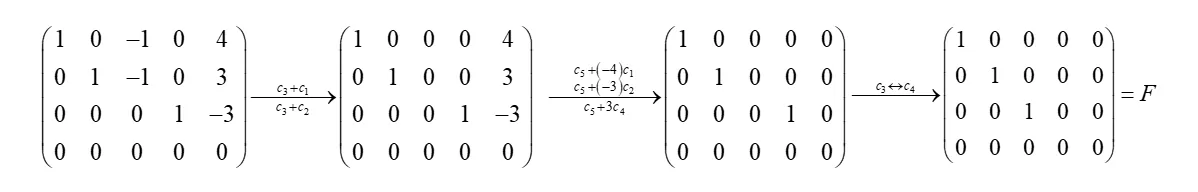
最后一个矩阵称为矩阵的标准形,写成分块矩阵的形式,则有
F=(E3ooo)
对于一般的矩阵,我们有下面的结论:
01任意一个 m×n 矩阵总可以经过若干次初等行变换化为行阶梯形矩阵;
02 任意一个 m×n 矩阵总可以经过若干次初等行变换化为行最简形矩阵;
03 任意一个 m×n 矩阵总可以经过若干次初等变换化为它标准形 F=(Er0o0)m,n,
04 其中 r 为行阶梯形矩阵中非零行的行数.
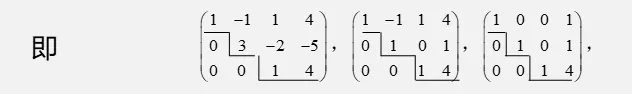


 {width=400px}
{width=400px}
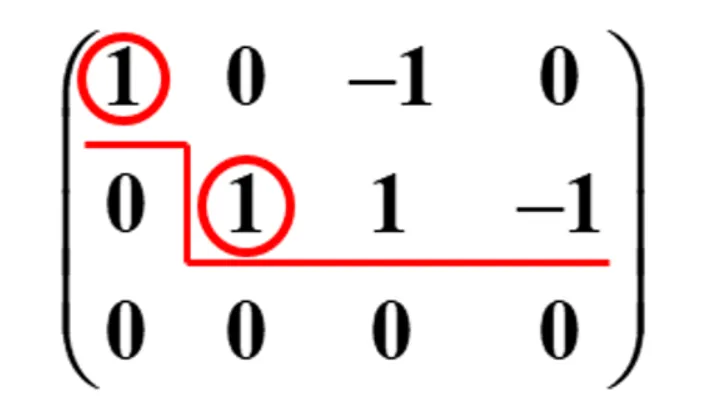 {width=200px}
{width=200px}