1._向量空间公式汇总

本章是线性代数较为抽象的一节，也是最难的一章，各种关系粉墨登场， 线性相关与线性无关-方程有解与无解-矩阵乘法与矩阵可逆-行列式值是否为零 这四者关系犹如《红楼梦》里的四大家族，一损俱损，一荣俱荣，而矩阵的秩Rank就犹如一根线，把他们给串联了起来

矩阵的秩：矩阵的秩犹如捆在猴子身上的绳索，矩阵的秩越大，表示捆的绳子就越多，猴子的灵活性就越低，当m=nm=n时，行列式为零，表示猴子已经没有灵活性了。每增加一个方程，就减少了一个灵活度，每减少一个方程，就增加了一个灵活度，这是一个矛盾的统一

线性代数中的三种变换-以值定性

图片

图片

图片

图片

图片

图片

图片

图片

图片

图片

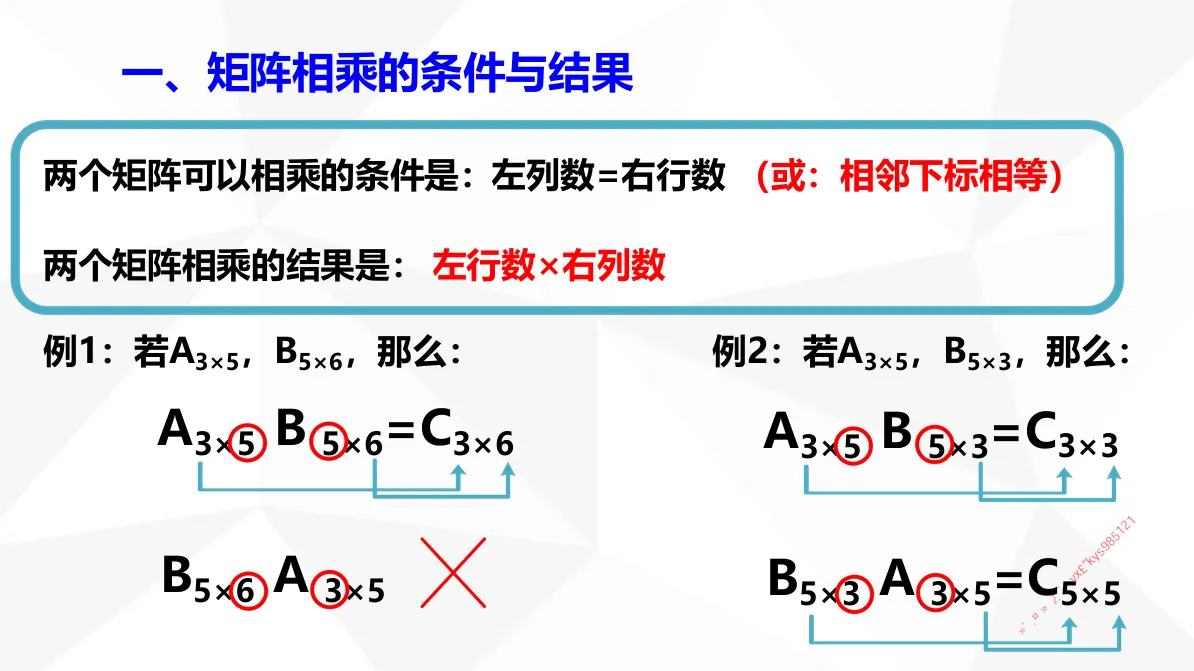
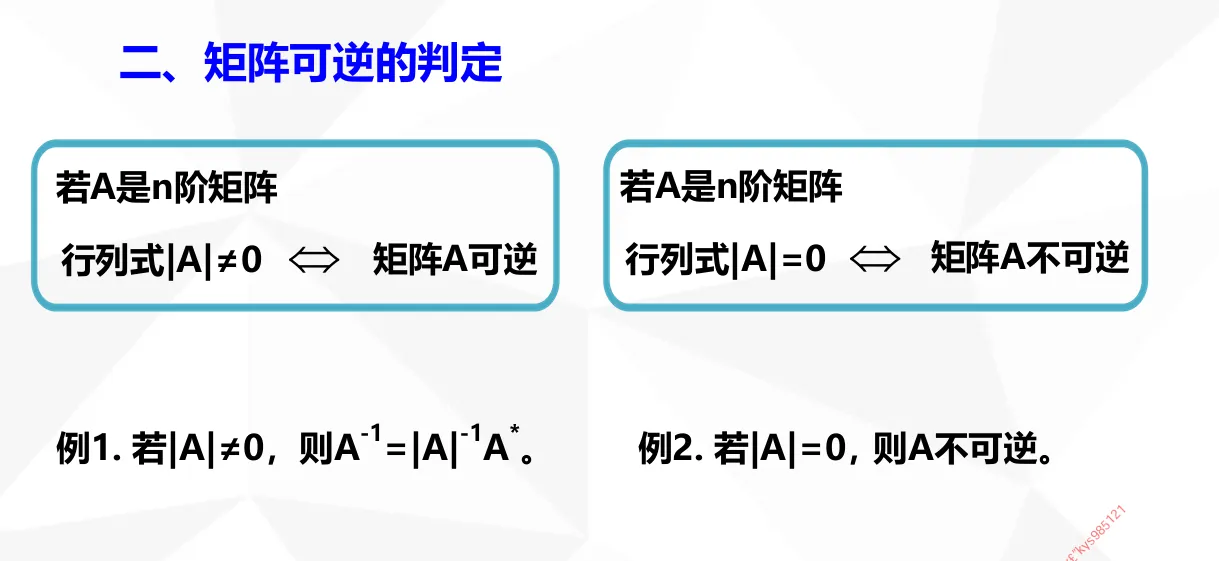
注①： 公式汇总主要参考 武忠祥 编制的 线性代数公式 注②： 图片汇总注意参考 西安电子科技大学教授杨威PPT，详见B站 线帒杨

线性表示

(1) 向量 β\boldsymbol{\beta} 可由 α1,α2,⋯ ,αm\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_m 线性表示

⇔ 定义 βj\stackrel{\text { 定义 }}{\Leftrightarrow} \boldsymbol{\beta}_j 存在数 k1,k2,⋯ ,kmk_1, k_2, \cdots, k_m, 使 β=k1α1+k2α2+⋯+kmαm\boldsymbol{\beta}=k_1 \boldsymbol{\alpha}_1+k_2 \boldsymbol{\alpha}_2+\cdots+k_m \boldsymbol{\alpha}_m ⇔\Leftrightarrow 线性方程组 x1α1+x2α2+⋯+xmαm=βx_1 \boldsymbol{\alpha}_1+x_2 \boldsymbol{\alpha}_2+\cdots+x_m \boldsymbol{\alpha}_m=\boldsymbol{\beta} 有解

⇔r(A)=r(A,β), 其中 A=(α1,α2,⋯ ,αm). \Leftrightarrow \mathrm{r}(\boldsymbol{A})=\mathrm{r}(\boldsymbol{A}, \boldsymbol{\beta}) \text {, 其中 } \boldsymbol{A}=\left(\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_m\right) \text {. }

(2) 向量组 β1,β2,⋯ ,βt\boldsymbol{\beta}_1, \boldsymbol{\beta}_2, \cdots, \boldsymbol{\beta}_t 可由 α1,α2,⋯ ,αm\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_m 线性表示 ⇔ 定义 βj\stackrel{\text { 定义 }}{\Leftrightarrow} \boldsymbol{\beta}_j 能由 α1,α2,⋯ ,αm\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_m 线性表示, j=1,2,⋯ ,tj=1,2, \cdots, t

⇔r(A)=r(A,B), 其中 A=(α1,α2,⋯ ,αm),B=(β1,β2,⋯ ,βt). \Leftrightarrow \mathrm{r}(\boldsymbol{A})=\mathrm{r}(\boldsymbol{A}, \boldsymbol{B}) \text {, 其中 } \boldsymbol{A}=\left(\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_m\right), \boldsymbol{B}=\left(\boldsymbol{\beta}_1, \boldsymbol{\beta}_2, \cdots, \boldsymbol{\beta}_t\right) \text {. }

(3) 向量组 α1,α2,⋯ ,αm\boldsymbol{\alpha}_1, \alpha_2, \cdots, \alpha_m 与 β1,β2,⋯ ,βt\beta_1, \beta_2, \cdots, \beta_t 等价 ⇔ 定义 α1,α2,⋯ ,αm\stackrel{\text { 定义 }}{\Leftrightarrow} \alpha_1, \alpha_2, \cdots, \alpha_m 与 β1,β2,⋯ ,βt\beta_1, \beta_2, \cdots, \beta_t 能互相线性表示 ⇔r(A)=r(B)=r(A,B)\Leftrightarrow \mathrm{r}(\boldsymbol{A})=\mathrm{r}(\boldsymbol{B})=\mathrm{r}(\boldsymbol{A}, \boldsymbol{B}), 其中 A=(α1,α2,⋯ ,αm),B=(β1,β2,⋯ ,βt)\boldsymbol{A}=\left(\boldsymbol{\alpha}_1, \alpha_2, \cdots, \alpha_m\right), \boldsymbol{B}=\left(\beta_1, \boldsymbol{\beta}_2, \cdots, \boldsymbol{\beta}_t\right) ⇔β1,β2,⋯ ,βt\Leftrightarrow \beta_1, \beta_2, \cdots, \beta_t 可由 α1,α2,⋯ ,αm\alpha_1, \alpha_2, \cdots, \alpha_m 线性表示, 且 r(A)=r(B)\mathrm{r}(\boldsymbol{A})=\mathrm{r}(\boldsymbol{B}).

详细教程参考 向量组的等价 与 向量组等价的几何意义

线性表示并不要求 k1,k2,...kmk_1,k_2,...k_m 一定不为零。或者说 线性表示包含了 线性相关与线性无关

线性相关

线性相关

nn 维向量组 α1,α2,⋯ ,αm\alpha_1, \alpha_2, \cdots, \alpha_m 线性相关 定义 ⇔\Leftrightarrow 存在一组不全为 0 的数 k1,k2,⋯ ,kmk_1, k_2, \cdots, k_m, 使 k1α1+k2α2+⋯+kmαm=0k_1 \boldsymbol{\alpha}_1+k_2 \boldsymbol{\alpha}_2+\cdots+k_m \boldsymbol{\alpha}_m=\mathbf{0} ⇔\Leftrightarrow 齐次线性方程组 x1α1+x2α2+⋯+xmαm=0x_1 \boldsymbol{\alpha}_1+x_2 \boldsymbol{\alpha}_2+\cdots+x_m \boldsymbol{\alpha}_m=\mathbf{0} 有非零解 ⇔\Leftrightarrow 至少有一个向量可由其余向量线性表示 ⇔r(α1,α2,⋯ ,αm)<m\Leftrightarrow \mathrm{r}\left(\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_m\right) < m ⇔m=n∣α1,α2,⋯ ,αm∣=0\stackrel{m=n}{\Leftrightarrow}\left|\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_m\right|=0.

线性无关

nn 维向量组 α1,α2,⋯ ,αm\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_m 线性无关 ⇔ 定义 \stackrel{\text { 定义 }}{\Leftrightarrow} 若 k1α1+k2α2+⋯+kmαm=0k_1 \boldsymbol{\alpha}_1+k_2 \boldsymbol{\alpha}_2+\cdots+k_m \boldsymbol{\alpha}_m=\mathbf{0}, 则必有 k1=k2=⋯=km=0k_1=k_2=\cdots=k_m=0 ⇔\Leftrightarrow 齐次线性方程组 x1α1+x2α2+⋯+xmαm=0x_1 \boldsymbol{\alpha}_1+x_2 \boldsymbol{\alpha}_2+\cdots+x_m \boldsymbol{\alpha}_m=\mathbf{0} 只有零解 ⇔\Leftrightarrow 任一向量都不能由其余向量线性表示 ⇔r(α1,α2,⋯ ,αm)=m\Leftrightarrow \mathrm{r}\left(\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_m\right)=m ⇔m=n∣α1,α2,⋯ ,αm∣≠0\stackrel{m=n}{\Leftrightarrow}\left|\alpha_1, \alpha_2, \cdots, \alpha_m\right| \neq 0.

线性相关的一些结论

(1) 如果向量组 α1,α2,⋯ ,αm\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_m 中有一部分向量线性相关, 则整个向量组也线性相关; 若 整个向量组也线性无关, 则部分向量组也线性无关. (简记为: 部分相关, 整体相关; 整体无关, 部分无关).

可以类比新冠疫情：班级发现病毒，则全校都的封锁。 如果全校都没封锁，则班级肯定也不封锁。

(2) 如果 α1,α2,⋯ ,αs\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_s 线性无关, 则 (α1β1),(α2β2),⋯ ,(αmβm)\left(\begin{array}{l}\boldsymbol{\alpha}_1 \\ \boldsymbol{\beta}_1\end{array}\right),\left(\begin{array}{l}\boldsymbol{\alpha}_2 \\ \boldsymbol{\beta}_2\end{array}\right), \cdots,\left(\begin{array}{l}\boldsymbol{\alpha}_m \\ \boldsymbol{\beta}_m\end{array}\right) 线性无关; 反之, 若 (α1β1),(α2β2),⋯ ,(αmβm)\left(\begin{array}{l}\boldsymbol{\alpha}_1 \\ \boldsymbol{\beta}_1\end{array}\right),\left(\begin{array}{l}\boldsymbol{\alpha}_2 \\ \boldsymbol{\beta}_2\end{array}\right), \cdots,\left(\begin{array}{l}\boldsymbol{\alpha}_m \\ \boldsymbol{\beta}_m\end{array}\right) 线性相关, 则 α1,α2,⋯ ,αs\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_s 线性相关. (简记为: 低维无关, 高维无关; 高维相关，低维相关. ) 可以类比亲戚关系。如果两个儿子之间没有亲戚关系，那么他们的父亲也没有亲戚关系。 如果父亲之间有亲戚关系，那么他们的儿子之间也有亲戚关系

(3) 若向量组 α1,α2,⋯ ,αr\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_r 线性无关, 而 β,α1,α2,⋯ ,αr\boldsymbol{\beta}, \boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_r 线性相关, 则 β\boldsymbol{\beta} 可由 α1,α2,⋯ ,αr\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_r 线性表示, 且表示法唯一.

(4) 若向量组 β1,β2,⋯ ,βt\boldsymbol{\beta}_1, \boldsymbol{\beta}_2, \cdots, \boldsymbol{\beta}_t 可由 α1,α2,⋯ ,αs\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_s 线性表示, 且 t>st>s, 则 β1,β2,⋯ ,βt\boldsymbol{\beta}_1, \boldsymbol{\beta}_2, \cdots, \boldsymbol{\beta}_t 线性相 关. （多的能由少的线性表示, 则多的必线性相关.）

若向量组 β1,β2,⋯ ,βt\boldsymbol{\beta}_1, \boldsymbol{\beta}_2, \cdots, \boldsymbol{\beta}_t 可由 α1,α2,⋯ ,αs\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_s 线性表示, 且 β1,β2,⋯ ,βt\boldsymbol{\beta}_1, \boldsymbol{\beta}_2, \cdots, \boldsymbol{\beta}_t 线性无关, 则 t≤st \leq s. (无关向量组不能由比它个数少的向量组表出. )

(5) n+1n+1 个 nn 维向量必相关. （考虑n=2n=2,则3个2维向量一定线性相关）

Previous3向量空间
Next2._向量的概念及运算