有了行列式和矩阵这两个话题的铺垫, 可以让线性代数的主人翁---向量出场了. 向量作为现代数学的基础,深深的渗透数学的各种学科,要了解平面向量,可以参考高中平面向量教程
向量的基本概念
我们在物理学中已经学过速度的有关知识, 知道表征速度需要两个参数:(1)速度的大小。(2)速度的方向。
既有大小又有方向的量我们称为向量 (也称为矢量),与此相对,只有大小没有方向的量叫做“标量”。 物理中,速度,力,位移都是向量,而质量,长度,电阻都是标量。
对应向量的大小也称为向量的模 (也可以叫向量长度);
对于同一个意义的名词,数学和物理有时候会采用不同的叫法。在数学里,把向量叫做向量,但是在物理里,叫做矢量,虽然名称不同,但是意义一样。
下图下述了一个简单的向量OA.
 {width=250px}
{width=250px}
我们知道, 位移可以用带箭头的线段 (即有向线段) 来直观地表示. 类似地, 我们也用有向线段来直观地表示向量, 其中有向线段的长度表示向量的大小简称模,(我们知道长度总是大于等于零的,所以向量的模总是大于等于零,他不会是负数), 有向线段箭头所指的方向表示向量的方向. 而且, 通常将有向线段不带箭头的端点称为向量的始点 (或起点), 带箭头的端点称为向量的终点.
向量的表示
有向线段始点和终点的相对位置确定向量的大小与方向. 始点为 A 终点为 B 的有向线段表示的向量, 可以用符号简记为 AB, 此时向量的模用 ∣AB∣ 表示.
除了用始点和终点的两个大写字母来表示向量外, 还可用一个小写字母来表示向量: 在印刷时, 通常用加粗的斜体小写字母如 a,b,c 等来表示向量 ; 在书写时, 用带箭头的小写字母如 a,b,c 等来表示向量. 此时, 向量 a 的模也用 ∣a∣ 或 ∣a∣ 来表示.
相反向量
向量AB 与 BA 虽然长度相等, 但方向相反, 因此 AB=BA.
类似于相反数的定义,我们把长度相等、方向相反的向量 a,b 称为相反向量,记作 b=−a 。如果 b=−a, 则同样也有 a=−b.
零向量
始点和终点相同的向量称为零向量. 零向量在印刷时, 通常用加粗的阿拉伯数字零表示, 即 0 ; 书写时, 通常用带箭头的阿拉伯数字零表示, 即 0. 不难看出, 零向量的模为 0 , 即
∣0∣=0. 零向量本质上是一个点, 因此可以认为零向量的方向是不确定的. 模不为 0 的向量通常称为非零向量.
单位向量
我们定义:模等于 1 的向量称为单位向量. 这就是说, 如果 e 是单位向量, 则
反之也成立. 因此, e 是单位向量的充要条件是 ∣e∣=1.
与非零向量 a 同方向的单位向量叫做向量 a 的单位向量, 记作 e. 根据实数与向量的乘法的定义, 可知 a=∣a∣e, 即
e=∣a∣1a. 这是一个重要的公式,在《线性代数》里,会用到
例三维向量 a=(1,1,1) ,求其单位向量。
解:该其模长为
D=12+12+12=3
所以,单位化后单位向量为
e=(31,31,31)
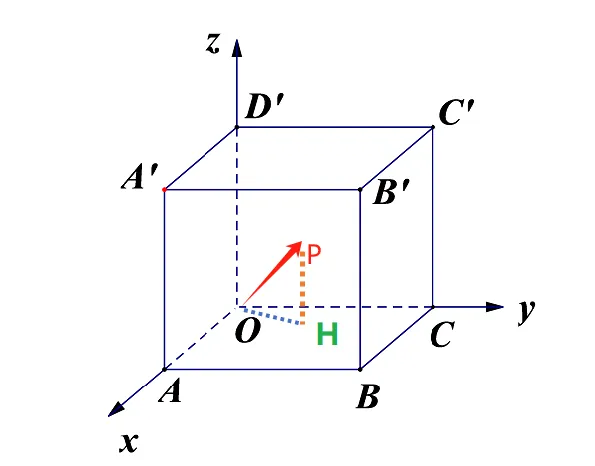
如果我们把向量a 放在三维空间里(参考下图),为了方便理解,这里加了一个立方体,你就可以看到,所谓a的模,就是向量OP的长度。
自P点往xoy平面进行投影,投影点为H,连接OH,所以△OPH 是直角三角形。
在Rt△OPH 里,可以得到 OP与xoy的夹角余弦值,即
cos∠POH=OPOH
 {width=400px}
{width=400px}
假设P(x,y,z) ,那么 OP=x2+y2+z2。
而OH又在xoy平面,所以,OH=x2+y2
因此,
P与xoy平面 的夹角余弦为
cos<P−xoy>=cos∠POH=x2+y2+z2x2+y2 同理,
P与yoz平面 的夹角余弦为
cos<P−yoz>=cos∠POH=x2+y2+z2y2+z2 P与xoz平面 的夹角余弦为
cos<P−yoz>=cos∠POH=x2+y2+z2x2+z2 这就是向量和平面的夹角余弦公式,换句话说,任给一个向量a,都可以求出他与三个坐标平面的夹角。
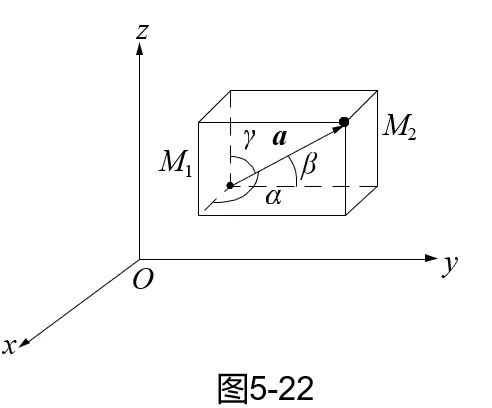
方向角与方向角余弦
通常我们使用向量和坐标轴的夹角,这个角度被称作方向角,参考下图
 {width=400px}
{width=400px}
其计算方法参考 高等数学里 方向角与方向余弦
向量的相等与平行
向量相等
我们定义:把大小相等、方向相同的向量称为相等的向量. 向量 a 和 b 相等, 记作
a=b. 向量平行
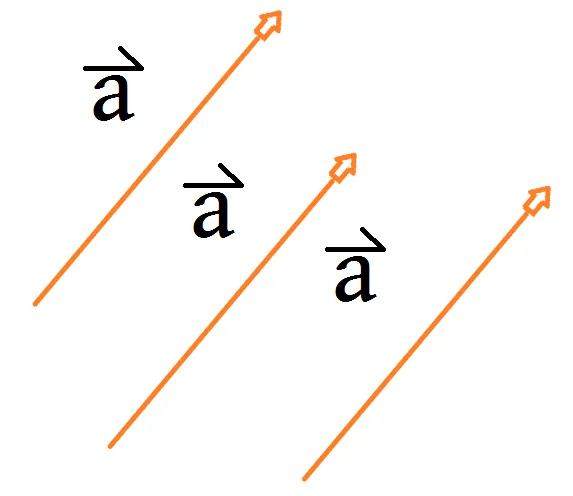
如果两个非零向量的方向相同或者相反,则称这两个向量平行.
 {width=250px}
{width=250px}
零向量
因为零向量的方向不确定, 所以通常规定零向量与任意向量平行.
我们约定,所有的零向量相等。
向量共线
两个向量 a 和 b 平行, 记作 a//b. 两个向量平行也称为两个向量共线.
向量的加法
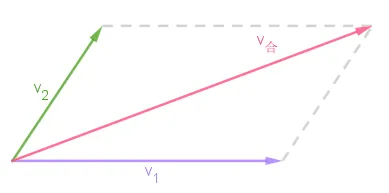
向量的加法最初来源于物理学中的 “速度" 或者 "力" 的合成。 如下图 v1 和 v2 最终合成了 v合 , 即: v1+v2=v合 , 这种计算方法也被叫做平行四边形法则。
 {width=250px}
另外一种是三角形法则,如下图,小明从 A 点走到 B 点,然后转弯走到 C 点 则,小明最终走的距离是 AC ,因此
{width=250px}
另外一种是三角形法则,如下图,小明从 A 点走到 B 点,然后转弯走到 C 点 则,小明最终走的距离是 AC ,因此
AB+BC=AC 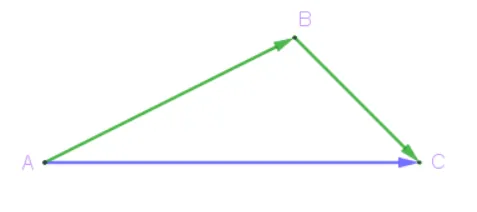 {width=250px}
{width=250px}
事实上,平行四边形法则和三角形法则并没有本质的区别,在上一节已经说过,两个向量只要大小相等,方向相同就是相同的向量,参考上图,在三角形法则里,把 BC 向左平移,让 B 点和 A 点重合,你就会发现三角形法则其实就是平行四边形法则。
向量加法满足交换律和结合律,即:
(1) 数乘 x(ya)=xya (后述)
(1) 加法交换律: a+b=b+a 对任意两个向量 a,b 成立.
(2) 加法结合律: (a+b)+c=a+(b+c) 对任意三个向量 a,b,c 成立.
向量的减法
在数学里,我们知道减去一个数其实等于加上这个数的相反数。同样,在向量里,规定与 a 大小相等,方向相反的向量,叫做 a 的相反向量,因此
a−b=a+(−b) 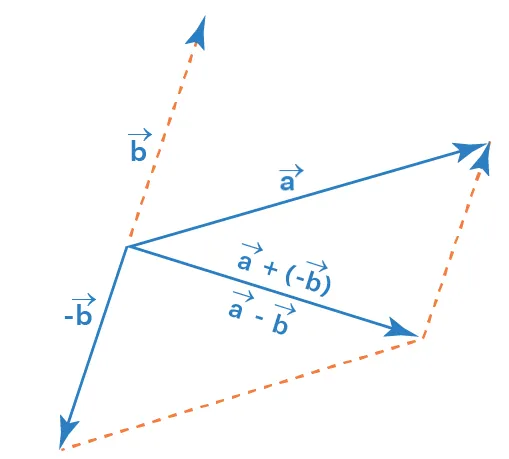 {width=250px}
{width=250px}
向量加减的区别
在使用三角形法则时,容易搞混向量是加法还是减法,这里给出一个小技巧。当给你一个向量三角形时,如何迅速判断他是向量加法还是减法呢?请看下面介绍。
向量加法
下图 a+b=c 里,三个向量以a的起点为起点,以b的终点为终点,最终是由a指向 b 。
记忆方法:小明从家到北京,再从北京到上海,那么最终小明走的结果就是从家到上海(也就是从起点指向终点,与中间环节无关)。
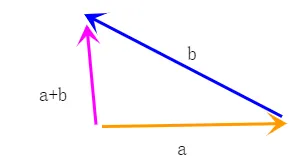
向量减法
下图 a−b=c 里,理解为以 b 的终点为始点,以 a 的终点为终点的向量,方向由b指向 a
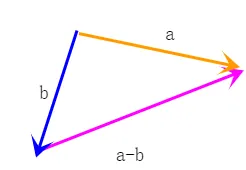
记忆技巧
海曼 • 格拉斯曼是德国的几何学家,他 1844 年发表的《延拓论》创立了现今的 n 维几何学。格拉斯曼在构建 n 维几何代数理论时是以一个非常简单的公式 AB+BC=AC (见图 2-15(a))作为研究起点的。他发现,上面介绍的三角形法则,如果不考虑线段点 A、B、C 的顺序, 只要不把 AB 、 BC 这样的因子仅仅理解为长度, 并且赋予它们 "方向" (例如 BA=−AB ), 公式依然正确。举个例子: 如果 C 位于 A 和 B 之间(见图 2-15 (b)),那么 AB=AC+CB ,但是由于 CB=−BC ,我们将发现 AB=AC−BC 。此时只要在这个公式两边简单地加上 BC 就能得到最初的公式 AB+BC=AC 。

也就是说图 2-15 的两个图例都有 AB+BC=AC 成立。
把图 2-15 的两根直线中间的 B 点和 C 点各自向上拉伸一些距离, 等式 AB+BC=AC 依然成立 (见图 2-16), 我们刚刚知道这就是向量的三角形加法法则。

继续向空间中拉伸就是三维向量乃至 n 维向量的加法了, 等式同样成立。
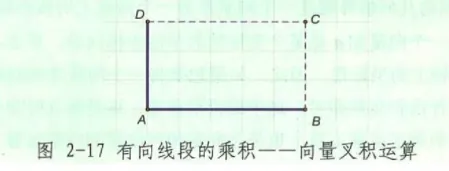
这是一个非常有价值的发现。但格拉斯曼对向量的延伸和拓展更加让人吃惊, 他拓展到向量的外积运算。比如, 如图 2-17 所示的正方形或平行四边形 ABCD, 如果正方形或平行四边形的面积 SABCD=AB⋅AD, 那么就有 AB⋅DA=−SABCD 成立。这正是后面将要介绍的向量的外积(叉积)运算及其几何意义。格拉斯曼由此最终发明了一种全新的被称之为外积代数的几何理论。
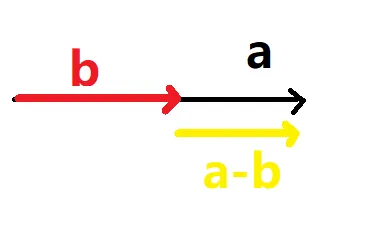
因此,对于向量减法的三角形法则,可以考虑特殊情况:即 a,b 共线的情况:如下图 黑色a减去红色b,等于黄色 a−b ,箭头指向a的方向
 {width=200px}
{width=200px}
向量的数乘
一般地, 给定一个实数 λ 与任意一个向量 a, 规定它们的乘积是一个向量, 记作 λa, 其中:
(1) 当 λ=0 且 a=0 时, λa 的模为 ∣λ∣∣a∣, 而且 λa 的方向如下:
{ 当 λ>0 时, 与 a 同向, 当 λ<0 时, 与 a 反向; (2) 当 λ=0 或 a=0 时, λa=0.
上述实数 λ 与向量 a 相乘的运算简称为数乘向量. 由定义不难看出, 数乘向量的结果是一个向量, 而且这个向量与原来的向量共线 (平行), 即 λa// a; 数乘向量的几何意义是, 把向量沿着它的方向或反方向放大或缩小. 特别地, 一个向量的相反向量可以看成 -1 与这个向量的乘积, 即 −a=(−1)a.
当 λ 和 μ 都是实数, 且 a 是向量时: μa 是向量, λ(μa) 也是向量; λμ是实数, 但 (λμ)a 是向量. 可以看出
λ(μa)=(λμ)a 另外,也可以证明
(λ+μ)a=λa+μa 和
\lambda(\vec{a}+\vec{b})=\lambda \vec{a}+\lambda \vec{b}$
我们把向量的加法、减法、数乘运算统称为向量的线性运算。
二维向量(平面向量)
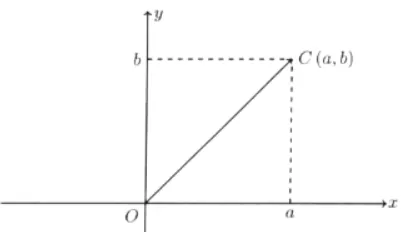
我们已经在高中平面向量里学过. 在一个平面上, 给点一个坐标点(a,b) 连接原点和坐标点,形成一个又向箭头,这样就形成二维平面向量。
 {width=300px}
{width=300px}
三维向量(空间向量)
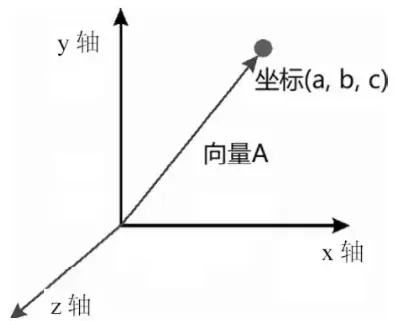
我们在高中空间向量 也学过, 给定空间一个坐标点(a,b,c),如下图,用一个又向箭头连接坐标原点和空间坐标点,将形成一个空间向量。
 {width=300px}
{width=300px}
n维向量
由二维和三维的概念,我们自然可以推广到n维,即 n 个数 a1,a2,⋯,an 组成的有序数组称为 n 维向量.
若 n 维向量写成 a1a2⋮an 的形式,称为 n 维列向量;
若 n 维向量写成 (a1,a2,⋯,an) 的形式,称为 n 维行向量.
这 n 个数称为该向量的 n 个分量,其中 ai 称为第 i 个分量.
分量都是零的向量称为零向量,记为0 。
我们常用 α,β,γ,… 来表示 n 维列向量,而用 α⊤,β⊤,γ⊤,… 来表示 n 维行向量.
向量 −a1−a2⋮−an 称为向量 α=a1a2⋮an 的负向量,记为 −α.
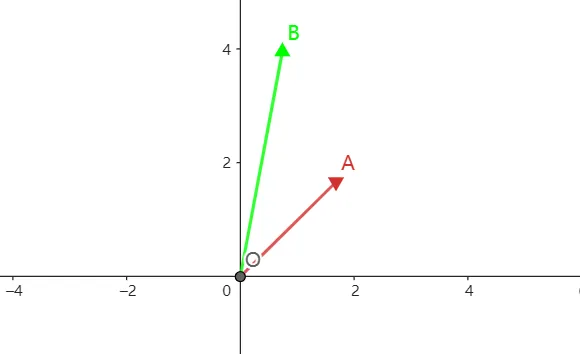
如下图 OA是由(2,2)T组成的2维向量,而OB则是由(1,4)T组成的另一个2维向量。
 {width=350px}
{width=350px}
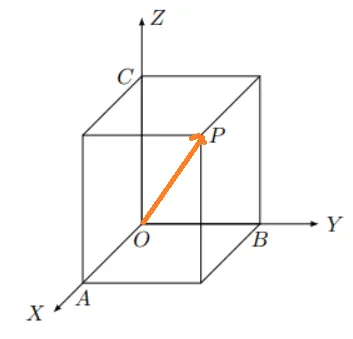
再如下图OP是由(2,2,3)T组成的3维向量。
 {width=300px}
{width=300px}
注意:《线性代数》里说到向量默认都是列向量。因此上面的记法 (2,2,3)T 其实是 223 ,虽然线性代数里,很多行向量的性质可以无缝移动到列向量上,而列向量的性质也可以无缝移动到行向量上,但是还是不建议把列向量和行向量混完一谈。
矩阵分解为列向量或行向量
有了向量以后,我们就可以从向量的角度看待矩阵。下面是一个3×4得矩阵:
A=123679246971 可以把他看成是4个列向量组成的矩阵(当然也可以看成3个行向量),即
α1=(123) α2=(679) α3=(246) α4=(971) 如果仔细看上面4个列向量,可以发现他们之间存在某种联系。
比如, 上面列向量里 α3=2α1, 这个α3向量可以由 α1 这个向量的 2 倍来表示,于是 α3 这个向量就是 “多余”的,不是独立的信息.
如果用G表示α1,α2,α3,α4 组成的集合,这个集合被称为向量组,在这个向量组G里,α1 和 α3 只要一个就可以了。比如要α1,那么向量组里的α3就可以用2α1来代替。
这种联系说到底就是线性无关的向量个数的问题,也就是若干个向量组成的向量组中,其中某几个就足够代表这个向量组了,其他的向量都可以由这几个向量线性表示出来(后面会详细叙述).
极大线性无关组
在一个向量组中, 能够代表该向量组中所有成员的一组向量被称为极大线性无关组,比如上面这个向量组G可以用
α1=(123) α2=(679) α4=(971) 这3个向量组表示。把它们组成的向量组叫作原向量组的极大线性无关组, 这个组就是原向量组的“代表”.
当然如果你使用
α2=(679) α3=(246) α4=(971) 作为极大线性无关组也是可以的。最主要的是,虽然他们形式不同,但是他们数量不变,都是3个。这个数字被称为向量组的秩。
极大线性无关组是向量组的“代表”, 而矩阵就是由向量组拼成的, 所以矩阵的秩、向量组的秩都反映了“代表”中向量的个数, 本质完全相同.
读者研读完这一部分就会得出下面这个重要结论:
我们要搞清楚向量与向量之间的关系---这种关系要么线性无关 (“独立”), 要么线性相关 (“多余”). 在充斥着诸多抽象理论和方法的向量组问题上, 只有把握住上述重要结论, 才不会迷失方向.
向量的运算
向量的运算性质
设 α=a1a2⋮an,β=b1b2⋮bn,k∈R ,则有
(1) α+β=a1+b1a2+b2⋮an+bn; (2) kα=ka1ka2⋮kan; (3) αTβ=(a1,a2,⋯,an)b1b2⋮bn=a1b1+a2b2+⋯+anbn (4)αβT=a1a2⋮an(b1,b2,⋯,bn)=a1b1a2b1⋮anb1a1b2a2b2⋮anb2⋯⋯⋱⋯a1bna2bn⋮anbn. 向量运算举例
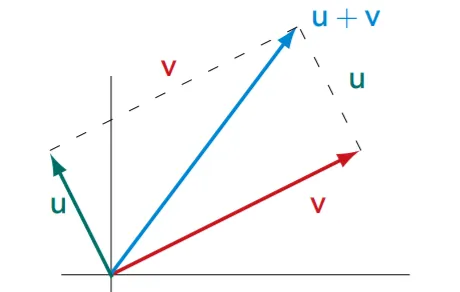
例 向量加法
[−12]+[42]=[34] 对应分量分别相加。
向量相加符合平行四边形法则。
 {width=300px}
{width=300px}
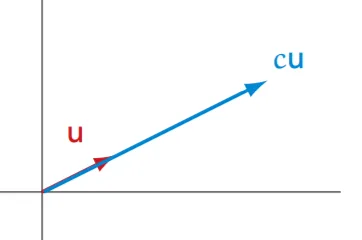
例向量数乘
3[21]=[63] 向量数乘反映向量的放大或者缩小。
 {width=300px}
{width=300px}
为什么我们默认使用列向量组
使用列向量组表示有很多好处,我们认为最主要的一个好处是和人类大脑的思维一直。(行向量更适合计算机思考模式),请看下面方程
设线性方程组
⎩⎨⎧a11x1+a12x2+⋯+a1nxn=b1a21x1+a22x2+⋯+a2nxn=b2⋮am1x1+am2x2+⋯+amnxn=bm 记
A=(aij)m×n=a11a21⋮am1a12a22⋮am2⋯⋯⋯a1na2n⋮amn,x=x1x2⋮xn,β=b1b2⋮bm, 我们就能立刻写出他的方差是
AX=B 这种写法和初中学过的代数式写法 ax=b 一致。
如果我们再把矩阵A的每一列看成一个向量,则有
Ax=(α1,α2,⋯,αn)x1x2⋮xn=β=x1α1+x2α2+⋯+xnαn 从而线性方程组 可表成如下形式:
x1a11a21⋮am1+x2a12a22⋮am2+⋯+xna1na2n⋮amn=b {width=250px}
 {width=400px}
{width=400px} {width=400px}
{width=400px} {width=250px}
{width=250px} {width=250px}
另外一种是三角形法则,如下图,小明从 点走到 点,然后转弯走到 点 则,小明最终走的距离是 ,因此
{width=250px}
另外一种是三角形法则,如下图,小明从 点走到 点,然后转弯走到 点 则,小明最终走的距离是 ,因此 {width=250px}
{width=250px} {width=250px}
{width=250px}




 {width=200px}
{width=200px} {width=300px}
{width=300px} {width=300px}
{width=300px} {width=350px}
{width=350px} {width=300px}
{width=300px} {width=300px}
{width=300px} {width=300px}
{width=300px}