10._极大线性无关组的求法

极大线性无关组的求法

本节通过例题来介绍给定一组向量里，求极大无关组的做法。

引理：矩阵的初等变换不改变向量间的线性关系。

证明：略。

定理的解释：若对 m×nm \times n 矩阵 AA 仅施以初等行变换化为矩阵 BB ，则 AA 的列向量组 α1,α2,⋯ ,αn\alpha_1, \alpha_2, \cdots, \alpha_n 同 BB 的列向量组 β1,β2,⋯ ,βn\beta_1, \beta_2, \cdots, \beta_n 有向完全相同的线性关系，即： 如果AA的某列向量可以表示为

αj=k1αj1+k2αj2+...+ksαjs\alpha_j=k_1 \alpha_{j_1}+k2 \alpha_{j_2}+...+k_s \alpha_{j_s}

则 BB 的列向量组 βj\beta_j 线性表示也可以表示为

βj=k1βj1+k2βj2+⋯+ksβjs\beta_j=k_1 \beta_{j_1}+k_2 \beta_{j_2}+\cdots+k_s \beta_{j_s}

反之，也是一样。 也就是他们的表示系数k1,k2,...ksk_1, k2, ...k_s 一样

现在开始做题。

例 求向量组 α1=(1,−2,2,−1),α2=(2,−4,8\alpha_1=(1,-2,2,-1), \alpha_2=(2,-4,8 ， 0),α3=(−2,4,−2,3),α4=(3,−6,0,−6)0), \alpha_3=(-2,4,-2,3), \alpha_4=(3,-6,0,-6) 的一个极大无关组，并给出其余向量用该极大无关组的表示。

解： STEP1: 把向量组按列排放，然后进行初等行变换，化为最简形 以 α1T,α2T,α3T,α4T\alpha_1^{ T }, \alpha_2^{ T }, \alpha_3^{ T }, \alpha_4^{ T } 为列向量作矩阵 AA ，并对 AA 施以初等行变换，把 AA 化为阶梯形矩阵 BB ：

A=[12−23−2−44−628−20−103−6]→[12−230000042−6021−3]→[12−23021−300000000]=B.A=\left[\begin{array}{rrrr} 1 & 2 & -2 & 3 \\ -2 & -4 & 4 & -6 \\ 2 & 8 & -2 & 0 \\ -1 & 0 & 3 & -6 \end{array}\right] \rightarrow\left[\begin{array}{rrrr} 1 & 2 & -2 & 3 \\ 0 & 0 & 0 & 0 \\ 0 & 4 & 2 & -6 \\ 0 & 2 & 1 & -3 \end{array}\right] \rightarrow\left[\begin{array}{rrrr} 1 & 2 & -2 & 3 \\ 0 & 2 & 1 & -3 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array}\right]=B .

继续对 BB 施以初等行变换，化为行简化阶梯形矩阵：

B=[12−23021−300000000]→[10−36021−300000000]→[β1β2β3β410−360112−3200000000]=C.B=\left[\begin{array}{rrrr} \\ 1 & 2 & -2 & 3 \\ 0 & 2 & 1 & -3 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array}\right] \rightarrow\left[\begin{array}{rrrr} \\ 1 & 0 & -3 & 6 \\ 0 & 2 & 1 & -3 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array}\right] \rightarrow\left[\begin{array}{cccc} \beta_1 & \beta_2 & \beta_3 & \beta_4 \\ 1 & 0 & -3 & 6 \\ 0 & 1 & \frac{1}{2} & -\frac{3}{2} \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array}\right]=C .

易见 β1,β2\beta_1, \beta_2 是列向量组 β1,β2,β3,β4\beta_1, \beta_2, \beta_3, \beta_4 的一个极大无关组，且有

β3=−3β1+12β2,β4=6β1−32β2.\beta_3=-3 \beta_1+\frac{1}{2} \beta_2, \beta_4=6 \beta_1-\frac{3}{2} \beta_2 .

使用行最简型的首非零元作为变量，其它作为自由变量作为最大线性无关组。如果你看表示的系数，恰是列向量的值，这不是偶然的，具体解释见 向量组的等价

图片

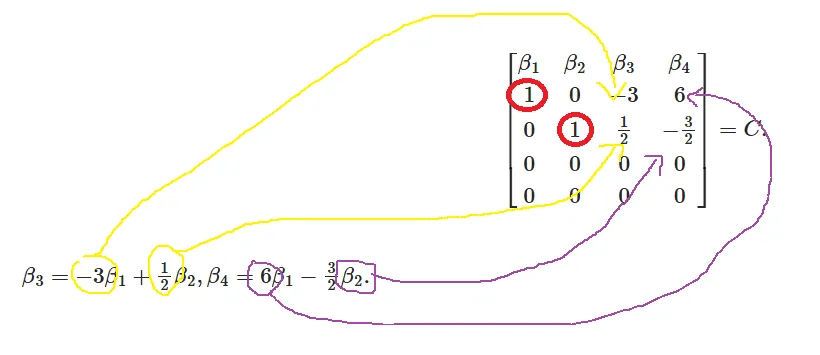
由上面引理知，α1,α2\alpha_1, \alpha_2 是 α1,α2,α3,α4\alpha_1, \alpha_2, \alpha_3, \alpha_4 的一个极大无关组，而且同样有

α3=−3α1+12α2,α4=6α1−32α2\alpha_3=-3 \alpha_1+\frac{1}{2} \alpha_2, \alpha_4=6 \alpha_1-\frac{3}{2} \alpha_2

例 设有向量组

α1=(1−21),α2=(2−42),α3=(103),α4=(0−4−4),\alpha _1=\left(\begin{array}{r} 1 \\ -2 \\ 1 \end{array}\right), \alpha _2=\left(\begin{array}{r} 2 \\ -4 \\ 2 \end{array}\right), \alpha _3=\left(\begin{array}{l} 1 \\ 0 \\ 3 \end{array}\right), \alpha _4=\left(\begin{array}{r} 0 \\ -4 \\ -4 \end{array}\right),

求该向量组的秩和它的一个极大无关组，并将其余向量用所求的极大无关组线性表示。

解：构造矩阵 A=(α1,α2,α3,α4)A =\left( \alpha _1, \alpha _2, \alpha _3, \alpha _4\right) ，对 AA 作初等行变换，将其化为简化的阶梯形矩阵，即

A=(a1a2a3a41210−2−40−4123−4)→ 初等行变换 (b1b2b3b41202001−20000)=B.A =\left(\begin{array}{rrrr} \boldsymbol{a_1} & a_2 & \boldsymbol{a_3} & a_4 \\ 1 & 2 & 1 & 0 \\ -2 & -4 & 0 & -4 \\ 1 & 2 & 3 & -4 \end{array}\right) \xrightarrow{\text { 初等行变换 }}\left(\begin{array}{rrrr} \boldsymbol{b_1} & b_2 & \boldsymbol{b_3} & b_4 \\ 1 & 2 & 0 & 2 \\ 0 & 0 & 1 & -2 \\ 0 & 0 & 0 & 0 \end{array}\right)= B .

显然，r(A)=r(B)=2r( A )=r( B )=2 ，即 r(α1,α2,α3,α4)=2r\left( \alpha _1, \alpha _2, \alpha _3, \alpha _4\right)=2 ．把上面最后一个矩阵 BB 记作 B=(β1,β2,β3,β4)B =\left( \beta _1, \beta _2, \beta _3, \beta _4\right) ．易见 β1,β3\beta _1, \beta _3 是 BB 的列向量组的一个极大无关组，它可以看作是矩阵 A1=(α1,α3)A _1=\left( \alpha _1, \alpha _3\right) 经初等行变换得到的，所以 α1,α3\alpha _1, \alpha _3 是 AA 的列向量组的一个极大线性无关组。

令 α2=k1α1+k3α3,α4=l1α1+l3α3\alpha _2=k_1 \alpha _1+k_3 \alpha _3, \alpha _4=l_1 \alpha _1+l_3 \alpha _3 ，利用简化的阶梯形矩阵 BB 求解这两个线性方程组，易得

k1=2,k3=0;l1=2,l3=−2k_1=2, k_3=0 ; l_1=2, l_3=-2

所以

α2=2α1,α4=2α1−2α3.\alpha_2=2 \alpha_1, \alpha_4=2 \alpha_1-2 \alpha_3 .

值得注意的是 α2\alpha _2 用 α1,α3\alpha _1, \alpha _3 表示的系数 2， 0 与 α4\alpha _4 用 α1,α3\alpha _1, \alpha _3 表示的系数 2,−22,-2 恰是简化的阶梯形矩阵 BB 的第二列与第四列的前两个元素．这不是偶然的（注意必须化为最简阶梯形）．因为解线性方程组 α2=k1α1+k3α3\alpha _2=k_1 \alpha _1+k_3 \alpha _3 等价于解线性方程组 β2=k1β1+k3β3\beta _2=k_1 \beta _1+k_3 \beta _3 ．解后面的线性方程组，相当于解以矩阵 BB 的第一列与第三列为系数矩阵，以第二列为常数项的线性方程组．由于矩阵 BB 为简化的阶梯形矩阵，去掉它的零行，与第一列和第三列对应的是单位矩阵，因而第二列的前两个元素即为方程组的解．同理，容易从矩阵 BB 得到线性方程组 α4=\alpha _4= l1α1+l3α3l_1 \alpha _1+l_3 \alpha _3 的解．

上面这个原理你不理解，直接死记也行， 你也可以在 向量组等价 里看解释

如果只需求向量组的秩和极大无关组，那么，只要用初等行变换将 AA 化为一般的阶梯形矩阵即可。

由解线性方程组的高斯消元法可知，对矩阵作初等行变换不改变它的列向量之间的线性关系；同理，对矩阵作初等列变换也不改变它的行向量之间的线性关系．

求基

例 A=[−36−11−71−223−12−458−4]\boldsymbol{A}=\left[\begin{array}{ccccc}-3 & 6 & -1 & 1 & -7 \\ 1 & -2 & 2 & 3 & -1 \\ 2 & -4 & 5 & 8 & -4\end{array}\right] ，求 A\boldsymbol{A} 的一组基．

解 利用初等行变换化 A\boldsymbol{A} 为行最简形矩阵：

A→[1−20−130012−200000],{x1−2x2−x4+3x5=0x3+2x4−2x5=00=0\boldsymbol{A} \rightarrow\left[\begin{array}{ccccc} 1 & -2 & 0 & -1 & 3 \\ 0 & 0 & 1 & 2 & -2 \\ 0 & 0 & 0 & 0 & 0 \end{array}\right], \quad\left\{\begin{array}{r} x_1-2 x_2-x_4+3 x_5=0 \\ x_3+2 x_4-2 x_5=0 \\ 0=0 \end{array}\right.

取 x2,x4,x5x_2, x_4, x_5 为自由变量，则解为

x1=2x2+x4−3x5,x3=−2x4+2x5.x_1=2 x_2+x_4-3 x_5, \quad x_3=-2 x_4+2 x_5 .

一般解的参数向量形式为

图片

上式说明 A={α,β,γ}\boldsymbol{A}=\{\boldsymbol{\alpha}, \boldsymbol{\beta}, \boldsymbol{\gamma}\} 。同时， α,β,γ\boldsymbol{\alpha}, \boldsymbol{\beta}, \boldsymbol{\gamma} 的构造方式保证了它们的线性无关性（考虑 0=x2α+x4β+x5γ\mathbf{0}=x_2 \boldsymbol{\alpha}+x_4 \boldsymbol{\beta}+x_5 \boldsymbol{\gamma} 的第2、4、5分量）．因此，{α,β,γ}\{\boldsymbol{\alpha}, \boldsymbol{\beta}, \boldsymbol{\gamma}\} 是 A\boldsymbol{A} 的一组基．

例求下面向量组的极大线性无关部分组：

α1=(2,0,1,1),α2=(−1,−1,−1,−1),α3=(1,−1,0,0),α4=(0,−2,−1,−1).\begin{array}{ll} \alpha_1=(2,0,1,1), & \alpha_2=(-1,-1,-1,-1), \\ \alpha_3=(1,-1,0,0), & \alpha_4=(0,-2,-1,-1) . \end{array}

解 把这向量组作为行排成一个矩阵，同时把该向量的希腊字母写在它的右方

A=[2011α1−1−1−1−1α21−100α30−2−1−1α4].A=\left[\begin{array}{rrrrr} 2 & 0 & 1 & 1 & \alpha_1 \\ -1 & -1 & -1 & -1 & \alpha_2 \\ 1 & -1 & 0 & 0 & \alpha_3 \\ 0 & -2 & -1 & -1 & \alpha_4 \end{array}\right] .

然后对上面的矩阵做行初等变换（现在不能做列初等变换了），在这过程中右边的用希腊字母标出的向量也跟着变。这样，在变换过程中，每个行向量永远等于右边用希腊字母表示的向量．

A→[1−100α32011α1−1−1−1−1α20−2−1−1α4]→[1−100α30211α1−2α30−2−1−1α2+α30−2−1−1α4]→[1−100α30211α1−2α30000α1+α2−α30000α1−2α3+α4].\begin{gathered} A \rightarrow\left[\begin{array}{rrrrr} 1 & -1 & 0 & 0 & \alpha_3 \\ 2 & 0 & 1 & 1 & \alpha_1 \\ -1 & -1 & -1 & -1 & \alpha_2 \\ 0 & -2 & -1 & -1 & \alpha_4 \end{array}\right] \rightarrow\left[\begin{array}{rrrcc} 1 & -1 & 0 & 0 & \alpha_3 \\ 0 & 2 & 1 & 1 & \alpha_1-2 \alpha_3 \\ 0 & -2 & -1 & -1 & \alpha_2+\alpha_3 \\ 0 & -2 & -1 & -1 & \alpha_4 \end{array}\right] \\ \rightarrow\left[\begin{array}{rrrrc} 1 & -1 & 0 & 0 & \alpha_3 \\ 0 & 2 & 1 & 1 & \alpha_1-2 \alpha_3 \\ 0 & 0 & 0 & 0 & \alpha_1+\alpha_2-\alpha_3 \\ 0 & 0 & 0 & 0 & \alpha_1-2 \alpha_3+\alpha_4 \end{array}\right] . \end{gathered}

矩阵化成阶梯形后，可看出其秩为 2 ，故原向量组的秩为 2 ，其极大线性无关部分组向量个数为 2 。另一个方面，最后两个行向量为零，这表示

α1+α2−α3=0,α1−2α3+α4=0\alpha_1+\alpha_2-\alpha_3=0, \quad \alpha_1-2 \alpha_3+\alpha_4=0

从这两个向量方程解出两个向量

α3=α1+α2;α4=α1+2α2.\alpha_3=\alpha_1+\alpha_2 ; \quad \alpha_4=\alpha_1+2 \alpha_2 .

于是整个向量组可被 α1,α2\alpha_1, \alpha_2 线性表示，因而原向量组与 α1,α2\alpha_1, \alpha_2 线性等价。已知其秩为2，那么 α1,α2\alpha_1, \alpha_2 的秩也是2，因而它线性无关。这说明 α1,α2\alpha_1, \alpha_2 即为原向量组的一个极大线性无关部分组．

Previous9._极大无关组及其几何意义
Next11._向量组秩的概念