11._向量组秩的概念

向量组秩的概念

在 向量组的等价 里说过，向量组的秩代表向量组成的维数。

假设给你nn个向量，如果这 nn 个向量的秩为1，就表示这nn个向量共线，反之也成立。

假设给你nn个向量，如果这 nn 个向量的秩为2，就表示这nn个向量在一个平面内，反之也成立。

假设给你nn个向量，如果这 nn 个向量的秩为3，就表示这nn个向量组成一个立方体，反之也成立。

以此类推，但是上面是通俗的解释，我们需要有严格的数学定义。

为了更好理解秩的概念，情况2个简单例子。

例nn 维单位坐标向量组 E:e1=(10⋮0),e2=(01⋮0),⋯ ,en=(00⋮1)E: \boldsymbol{e}_1=\left(\begin{array}{l}1 \\ 0 \\ \vdots \\ 0\end{array}\right), \boldsymbol{e}_2=\left(\begin{array}{l}0 \\ 1 \\ \vdots \\ 0\end{array}\right), \cdots, \boldsymbol{e}_n=\left(\begin{array}{l}0 \\ 0 \\ \vdots \\ 1\end{array}\right) 线性无关， 所以该向量组的极大无关组就是它本身.

例设向量组 A:α1=(223),α2=(152),α3=(4127)A: \boldsymbol{\alpha}_1=\left(\begin{array}{l}2 \\ 2 \\ 3\end{array}\right), \boldsymbol{\alpha}_2=\left(\begin{array}{l}1 \\ 5 \\ 2\end{array}\right), \boldsymbol{\alpha}_3=\left(\begin{array}{l}4 \\ 12 \\ 7\end{array}\right) 向量 α1\alpha_1 与 α2\alpha_2 的分量不对应成比例， 所以 α1,α2\alpha_1, \alpha_2 线性无关. 另外，由于 α3=α1+2α2\alpha_3=\alpha_1+2 \alpha_2 所以向量组 α1,α2,α\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \boldsymbol{\alpha} 线性相关. 向量组 α1,α2\alpha_1, \alpha_2 是向量组 α1,α2,α3\alpha_1, \alpha_2, \alpha_3 的极大无关组.

类似的讨论可知，向量组 α2,α3\alpha_2, \alpha_3 ， 向量组 α1,α3\alpha_1, \alpha_3 都可作为向量组 α1,α2,α3\alpha_1, \alpha_2, \alpha_3 的极大无关 组. 也就是说，一个向量组的极大无关组并不是唯一的. 向量组与其任意一个极大无关 组是相互等价的，由向量组等价的传递性可知，向量组的任意两个极大无关组相互等价. 向量组的每一个极大无关组所含向量的个数总是相等的. 于是，我们引入如下定义:

向量组秩的定义

向量组 AA 的任意一个极大无关组所含向量的个数，称为这个向量组的秩，记为 RAR_A

例如，例1中的向量组的秩 RE=nR_E=n ，例 2 中的向量组的秩 RA=2R_A=2

如果一个向量组只含有零向量，则它没有极大无关组，此时我们规定它的秩为零.

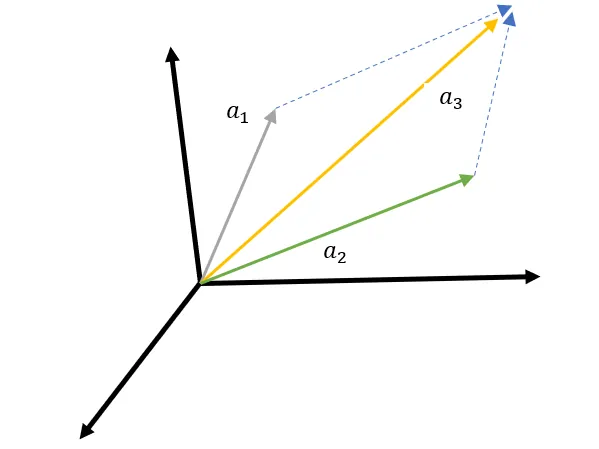
上面说过，秩等于维数，在例2里，他的秩为2，表示这3个向量共面，我们可以在三维空间里把这3个向量画出来。

α1=(223),α2=(152),α3=(4127)\boldsymbol{\alpha}_1=\left(\begin{array}{l}2 \\ 2 \\ 3\end{array}\right), \boldsymbol{\alpha}_2=\left(\begin{array}{l}1 \\ 5 \\ 2\end{array}\right), \boldsymbol{\alpha}_3=\left(\begin{array}{l}4 \\ 12 \\ 7\end{array}\right)

示意图如下，可以看到 α1,α2\alpha_1,\alpha_2 所张的平面，包含了α3\alpha_3. 当然你也可以说 α2,α3\alpha_2,\alpha_3 所张的平面，包含了α1\alpha_1 这不重要，重要的是这3个向量，要2个就可以了。

图片{width=400px}

推论1： 对于一组向量 α1,α2,...αs\alpha_1,\alpha_2,...\alpha_s 具有 0≤秩≤s0 \le 秩 \le s

推论2 α1,α2,...αs\alpha_1,\alpha_2,...\alpha_s 线性无关 等价于r(α1,α2,...αs)=sr(\alpha_1,\alpha_2,...\alpha_s)=s

推论3 α1,α2,...αs\alpha_1,\alpha_2,...\alpha_s 线性相关 等价于r(α1,α2,...αs)<sr(\alpha_1,\alpha_2,...\alpha_s)<s

记忆技巧：向量组的秩犹如绑在猴子身上的绳子，向量组的秩越大，表示绑定的绳子越多，猴子的自由度就越少，各个维度被限定了就线性就无关。 向量组的秩越小，表示绑定的绳子少，猴子就越灵活，各个维度可以自由活动，此时就线性相关。

定理 等价的向量组有相同的秩.

证明 因为每个向量组都与它的极大无关组等价，根据向量组等价的传递性， 任意两个等价的向量组的极大无关组也等价，因而有相同的秩.

例证明: 一个向量组线性无关的充分必要条件是它的秩等于它所含向量的个数. 证明：如果一个向量组本身线性无关，则这个向量组的极大无关组就是它自身，于是它的秩等于它所含向量的个数; 如果一个向量组的秩等于它所含向量的个数，则这个向量组显然是线性无关的.

例证明: 任 一nn维向量组 AA的秩 RA≤n R_A \leq n. 证明 因为 n+1n+1 个 nn 维向量必定线性相关， 所以 nn 维向量组 AA 的极大无关组中所含向量个数不能超过 nn 个， 即 RA≤nR_A \leq n.

例 证明向量组 α,β,γ\boldsymbol{\alpha}, \boldsymbol{\beta}, \boldsymbol{\gamma} 线性无关的充分必要条件是向量组

α+β,β+γ,γ+α\boldsymbol{\alpha}+\boldsymbol{\beta}, \boldsymbol{\beta}+\boldsymbol{\gamma}, \boldsymbol{\gamma}+\boldsymbol{\alpha}

线性无关． 证明：设

{ξ=α+βη=β+γζ=γ+α\left\{\begin{array}{l} \xi=\alpha+\beta \\ \eta=\beta+\gamma \\ \zeta=\gamma+\alpha \end{array}\right.

则有

{α=12(ξ−η+ζ)β=12(ξ+η−ζ)γ=12(−ξ+η+ζ)\left\{\begin{array}{l} \boldsymbol{\alpha}=\frac{1}{2}(\boldsymbol{\xi}-\boldsymbol{\eta}+\boldsymbol{\zeta}) \\ \boldsymbol{\beta}=\frac{1}{2}(\boldsymbol{\xi}+\boldsymbol{\eta}-\boldsymbol{\zeta}) \\ \boldsymbol{\gamma}=\frac{1}{2}(-\boldsymbol{\xi}+\boldsymbol{\eta}+\boldsymbol{\zeta}) \end{array}\right.

向量组 α,β,γ\boldsymbol{\alpha}, \boldsymbol{\beta}, \boldsymbol{\gamma} 与 ξ,η,ζ\boldsymbol{\xi}, \boldsymbol{\eta}, \boldsymbol{\zeta} 等价，从而有相同的秩．所以

α,β,γ 线性无关 ⇔r(α,β,γ)=3⇔r(ξ,η,ζ)=r(α+β,β+γ,γ+α)=3⇔α+β,β+γ,γ+α 线性无关. \begin{aligned} \boldsymbol{\alpha}, \boldsymbol{\beta}, \boldsymbol{\gamma} \text { 线性无关 } & \Leftrightarrow r(\boldsymbol{\alpha}, \boldsymbol{\beta}, \boldsymbol{\gamma})=3 \\ & \Leftrightarrow r(\boldsymbol{\xi}, \boldsymbol{\eta}, \boldsymbol{\zeta})=r(\boldsymbol{\alpha}+\boldsymbol{\beta}, \boldsymbol{\beta}+\boldsymbol{\gamma}, \boldsymbol{\gamma}+\boldsymbol{\alpha})=3 \\ & \Leftrightarrow \boldsymbol{\alpha}+\boldsymbol{\beta}, \boldsymbol{\beta}+\boldsymbol{\gamma}, \boldsymbol{\gamma}+\boldsymbol{\alpha} \text { 线性无关. } \end{aligned}

定理 如果一个向量组的秩为 r(r>0)r(r>0) ，则向量组中任意 rr个线性无关的向量都是它的一个极大无关组．

证明：设向量组 α1,α2,⋯ ,αm\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_m 的秩为 rr ，且 αi1,αi2,⋯ ,αir\boldsymbol{\alpha}_{i_1}, \boldsymbol{\alpha}_{i_2}, \cdots, \boldsymbol{\alpha}_{i_r} 是 α1,α2,⋯ ,αm\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_m 中 rr 个线性无关的向量．设 αk\boldsymbol{\alpha}_k 是向量组中任一个向量，则

αi1,αi2,⋯ ,αit,αk\boldsymbol{\alpha}_{i_1}, \boldsymbol{\alpha}_{i_2}, \cdots, \boldsymbol{\alpha}_{i_t}, \boldsymbol{\alpha}_k

线性相关，否则与 r(α1,α2,⋯ ,αm)=rr\left(\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_m\right)=r 相矛盾．可知， αk\boldsymbol{\alpha}_k可由 αi1,αi2,⋯ ,αir\boldsymbol{\alpha}_{i_1}, \boldsymbol{\alpha}_{i_2}, \cdots, \boldsymbol{\alpha}_{i_r} 线性表示．由定义， αi1,αi2,⋯ ,αir\boldsymbol{\alpha}_{i_1}, \boldsymbol{\alpha}_{i_2}, \cdots, \boldsymbol{\alpha}_{i_r} 为向量组的一个极大无关组．

定理

设向量组 α1,α2,⋯ ,α\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha} 可由向量组 β1,β2,⋯ ,βt\boldsymbol{\beta}_1, \boldsymbol{\beta}_2, \cdots, \boldsymbol{\beta}_t 线性表示，则

r(α1,α2,⋯ ,αs)⩽r(β1,β2,⋯ ,βt)r\left(\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_s\right) \leqslant r\left(\boldsymbol{\beta}_1, \boldsymbol{\beta}_2, \cdots, \boldsymbol{\beta}_t\right)

证明：设向量组 α1,α2,⋯ ,αs\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_s 与向量组 β1,β2,⋯ ,βt\boldsymbol{\beta}_1, \boldsymbol{\beta}_2, \cdots, \boldsymbol{\beta}_t 的极大无关组分别为 αi1,αi2,⋯ ,αir\boldsymbol{\alpha}_{i_1}, \boldsymbol{\alpha}_{i_2}, \cdots, \boldsymbol{\alpha}_{i_r} 与 βj1,βj2,⋯ ,βjk\boldsymbol{\beta}_{j_1}, \boldsymbol{\beta}_{j_2}, \cdots, \boldsymbol{\beta}_{j_k} ，则

αi1,αi2,⋯ ,αir 与 α1,α2,⋯ ,αs 等价, βj1,βj2,⋯ ,βjk 与 β1,β2,⋯ ,βt 等价. \begin{aligned} & \boldsymbol{\alpha}_{i_1}, \boldsymbol{\alpha}_{i_2}, \cdots, \boldsymbol{\alpha}_{i_r} \text { 与 } \boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_s \text { 等价, } \\ & \boldsymbol{\beta}_{j_1}, \boldsymbol{\beta}_{j_2}, \cdots, \boldsymbol{\beta}_{j_k} \text { 与 } \boldsymbol{\beta}_1, \boldsymbol{\beta}_2, \cdots, \boldsymbol{\beta}_t \text { 等价. } \end{aligned}

因此， αi1,αi2,⋯ ,αir\boldsymbol{\alpha}_{i_1}, \boldsymbol{\alpha}_{i_2}, \cdots, \boldsymbol{\alpha}_{i_r} 可由 βj1,βj2,⋯ ,βjk\boldsymbol{\beta}_{j_1}, \boldsymbol{\beta}_{j_2}, \cdots, \boldsymbol{\beta}_{j_k} 线性表示，由推论知，r⩽kr \leqslant k ，即

r(α1,α2,⋯ ,αs)⩽r(β1,β2,⋯ ,βt)r\left(\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_s\right) \leqslant r\left(\boldsymbol{\beta}_1, \boldsymbol{\beta}_2, \cdots, \boldsymbol{\beta}_t\right)
Previous10._极大线性无关组的求法
Next12._矩阵的秩的意义_向量版