3._集合论与向量空间

从集合的角度看向量

现在我们从集合的角度理解nn维向量。

一个二维向量，可以看成二维平面上箭头的集合。 图片{width=200px}

一个三维向量，可以看成三维空间上箭头的集合。 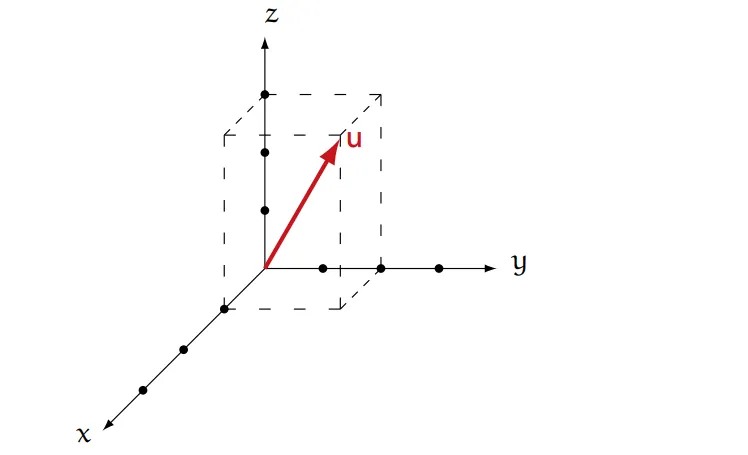图片{width=300px}

由此推广，一个nn维向量，可以看成nn维上形成的箭头的集合。

因此，我们定义一个集合：

集合={xx| x∈x \in 所有箭头 }

这样，不管是一维，二维，还是三维，nn维，所有的箭头组成得集合都在这个定义里，我们把这个集合命名为“向量空间”

在向量空间里，可以定义运算法则、向量的长度、向量之间的夹角、举例等，具体列表如下

图片

RnR^n向量空间（也称线性空间）

为了把上面的定义代数化，通常使用代数式表示向量空间。 我们先看两个重要的例子． 例R2R ^2 和 R3R ^3 集合 R2R ^2（你可以将其视作一个平面）是全体有序实数对所构成的集合：

R2={(x1,x2):x1,x2∈R}.R ^2=\{(x_1, x_2): x_1, x_2 \in R \} .

集合 R3R ^3（你可以将其视作通常的三维空间）是全体有序实数三元组所构成的集合：

R3={(x1,x2,x3):x1,x2,x3∈R}.R ^3=\{(x_1, x_2, x_3): x_1, x_2, x_3 \in R \} .

推广 由二维和三维，推广到nn维： RnR ^n 是全体具有 nn 个 RR 中元素的组所构成的集合：

Rn={(x1,…,xn): 对于 k=1,…,n 有 xk∈R}. R ^n=\left\{\left(x_1, \ldots, x_n\right): \text { 对于 } k=1, \ldots, n \text { 有 } x_k \in R \right\} \text {. }

对于 (x1,…,xn)∈Rn\left(x_1, \ldots, x_n\right) \in R ^n 和 k∈{1,…,n}k \in\{1, \ldots, n\} ，我们称 xkx_k 是 (x1,…,xn)\left(x_1, \ldots, x_n\right) 的第 kk 个坐标．

如果 n≥4n \geq 4 ，我们就无法将 RnR ^n 可视化为物理实体；然而，即便 nn 很大，我们也可以如在 R2R ^2 或 R3R ^3 中那样简便地在 FnF ^n 中进行代数运算．

向量空间的定义 设 K\mathbb{K} 是一个数域，VV 是一个集合，在 VV 上定义了一个加法＂+ ＂，即对 VV 中任意两个元素 α,β\boldsymbol{\alpha}, \boldsymbol{\beta} ，总存在 VV 中唯一的元素 γ\boldsymbol{\gamma} 与之对应，记为 γ=α+β\boldsymbol{\gamma}= \boldsymbol{\alpha}+\boldsymbol{\beta} ．

在数域 K\mathbb{K} 与 VV 之间定义了一种运算，称为数乘，即对 K\mathbb{K} 中任一数 kk 及 VV中任一元素 α\boldsymbol{\alpha} ，在 VV 中总有唯一的元素 δ\boldsymbol{\delta} 与之对应，记为 δ=kα\boldsymbol{\delta}=k \boldsymbol{\alpha} ．

若上述加法及数乘满足下列运算八大规则： （1）加法交换律： α+β=β+α\boldsymbol{\alpha}+\boldsymbol{\beta}=\boldsymbol{\beta}+\boldsymbol{\alpha} ； （2）加法结合律：(α+β)+γ=α+(β+γ)(\boldsymbol{\alpha}+\boldsymbol{\beta})+\boldsymbol{\gamma}=\boldsymbol{\alpha}+(\boldsymbol{\beta}+\boldsymbol{\gamma}) ； （3）在 VV 中存在一个元素 0\mathbf{0} ，对于 VV 中任一元素 α\boldsymbol{\alpha} ，都有 α+0=α\boldsymbol{\alpha}+\mathbf{0}=\boldsymbol{\alpha} ； （4）对于 VV 中每个元素 α\boldsymbol{\alpha} ，存在元素 β\boldsymbol{\beta} ，使 α+β=0\boldsymbol{\alpha}+\boldsymbol{\beta}=\mathbf{0} ； （5） 1⋅α=α1 \cdot \boldsymbol{\alpha}=\boldsymbol{\alpha} ； （6）k(α+β)=kα+kβk(\boldsymbol{\alpha}+\boldsymbol{\beta})=k \boldsymbol{\alpha}+k \boldsymbol{\beta} ； （7）(k+l)α=kα+lα(k+l) \boldsymbol{\alpha}=k \boldsymbol{\alpha}+l \boldsymbol{\alpha} ； （8）k(lα)=(kl)αk(l \boldsymbol{\alpha})=(k l) \boldsymbol{\alpha} ，

其中 α,β,γ\boldsymbol{\alpha}, \boldsymbol{\beta}, \boldsymbol{\gamma} 是 VV 中任意的元素，k,lk, l 是 K\mathbb{K} 中任意的数，则集合 VV 称为数域 K\mathbb{K} 上的线性空间或向量空间。

VV 中的元素称为向量，VV 中适合（3）的元素 0\mathbf{0} 称为零向量．对 VV 中的元素 α\boldsymbol{\alpha} ，适合 α+β=0\boldsymbol{\alpha}+\boldsymbol{\beta}=\mathbf{0} 的元素 β\boldsymbol{\beta} 称为 α\boldsymbol{\alpha} 的负向量，记为 −α-\boldsymbol{\alpha} ．

向量空间的运算

向量支持如下向量规则：

图片

上述规则可以简化为两大规则：加法规则和乘法规则，支持上述规则的运算被称为线性运算，也被称作线性空间。

n维子空间

让我们从一个简单的例子看起。考察 R2R ^2 中的子集：

  • L1={(x,0)∣x∈R}L _1=\{(x, 0) \mid x \in R \} 也是一个向量空间。

  • L2={(x,x+1)∣x∈R}L _2=\{(x, x+1) \mid x \in R \} 不是一个向量空间。

显然并不是所有的子集都是向量空间。后者之所以不是向量空间是因为没有过原点，我们称过原点的这样的子集为子空间。

从某种意义上说， nn维向量就像是一个枝繁叶茂的大树所构成的一个庞大物理空间。

为了方便理解，我们以3维空间为例。在3维向量空间这所大房子里又可以划分出好多居室，每个居室里的向量们也严格坚守着自己居室的同样的两项基本原则：相加和缩放不能超出自己的居室, 这些大大小小的居室就是子空间。 需要注意的是, 这些居室有个特点, 就是共有一个原点, 或者说都要包括零向量。空间和子空间的图形大致有如图 4-16所示的几种类型。 图片

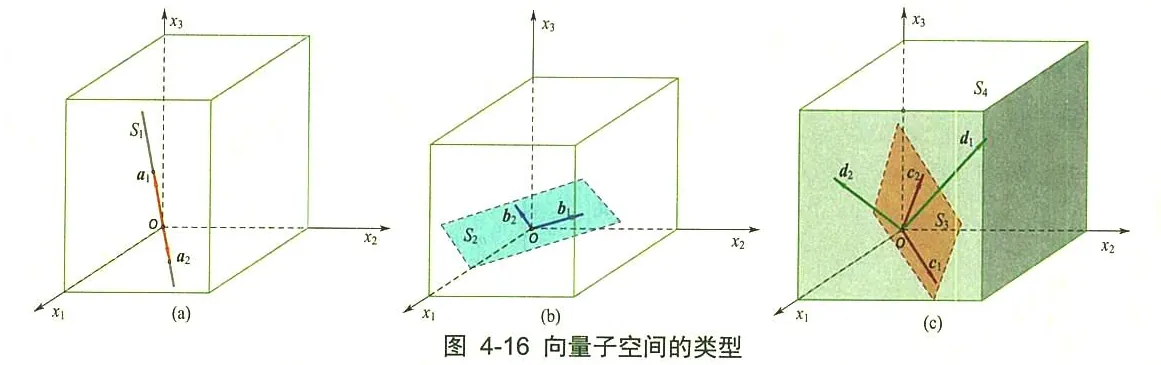
三维向量空间 R3R ^3 的所有子空间包括: ①三维子空间：本身 R3=Span⁡{α1,α2,α3}(α1、α2、α3R ^3=\operatorname{Span}\left\{\alpha_1, \alpha_2, \alpha_3\right\} \quad\left(\alpha_1 、 \alpha_2 、 \alpha_3\right. 线性无关），作为自身的子空间表现为一个立体空间, 同自身一样, 也包含原点;

②二维子空间：如 Span⁡{α1,α2}\operatorname{Span}\left\{\alpha_1, \alpha_2\right\} （ α1、α2\alpha_1 、 \alpha_2 线性无关），表现为通过原点的任意一个平面 （特别需要注意：二维空间 R2R ^2 不是 R3R ^3 的子空间 ，R2R^2 表示的是(1,0)(1,0)和(0,1)(0,1)张成的平面，这里二维子空间是(1,0,0)(1,0,0)和(0,1,0)(0,1,0)张成的平面);

③一维子空间：如 Span⁡{α1}(α1≠0)\operatorname{Span}\left\{\alpha_1\right\}\left( \alpha _1 \neq 0 \right) ，表现为通过原点的任意一条直线；

零维子空间：只包含原点 0 向量，只有零空间。

考察如下集合：

V=R3W={(x,y,0)∣x,y∈R}\begin{aligned} V & = R ^3 \\ W & =\{(x, y, 0) \mid x, y \in R \} \end{aligned}

则 WW 是 VV 的一个子空间，原因在于：

  • 对于任意的 u=(x1,y1,0),v=(x2,y2,0)∈W,u+v=(x1+x2,y1+y2,0)∈Wu =\left(x_1, y_1, 0\right), v =\left(x_2, y_2, 0\right) \in W , u + v =\left(x_1+x_2, y_1+y_2, 0\right) \in W 。

  • 对于任意的 c∈Rc \in R 和 u=(x,y,0)∈W,cu=(cx,cy,0)∈Wu =(x, y, 0) \in W , c u =(c x, c y, 0) \in W 。

更详细理解，请参考 线性空间及其子空间

向量空间代数化

每一个nn维向量，可以用nn维坐标来表示。 比如 α=(1,2,3,4)\alpha=(1,2,3,4) 可以表示四维空间里的一个向量。

这种把向量 "代数化" 的方法有着明显的好处: 一是可以用代数的工具来研几何对象; 二是它可以推广到更一般的情形，即所谓的 nn 维向量。 在比如3维空间P(a,b,c)P(a,b,c) 如下图，OP⃗\vec{OP}和(a,b,c)(a,b,c)有序实数对一一对应。

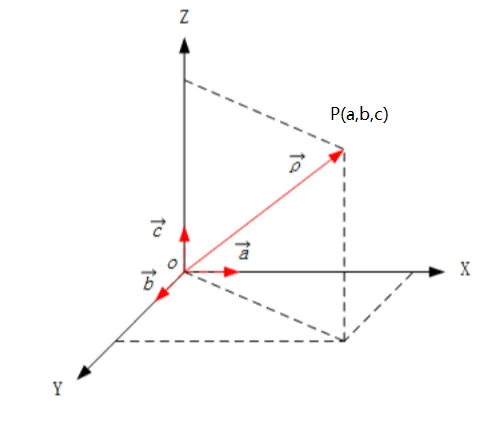图片{width=300px}

这种推广不仅是形式上的，而且它对于数学的发展及应用起着极其重要的作用。

例题

例 证明 f(x)=2xf(x)=2x 是线性空间 证明：要证明 f(x)=2xf(x)=2x 他是线性空间，只要证明支持加法和乘法规则即可。取任意实数a,ba,b， 容知道 f(a)=2af(a)=2a f(b)=2bf(b)=2b 所以， f(a∗b)=2a∗2b=4ab...①f(a*b)=2a * 2b =4ab ...① 又f(a)∗f(b)=2a∗2b=4ab...②f(a)*f(b)=2a*2b=4ab ...② 由①② 得 f(a∗b)=f(a)∗f(b)f(a*b)=f(a)*f(b) ，表明f(x)f(x)支持乘法运算

又 f(a)+f(b)=2a+2b=f(a+b)f(a)+f(b)=2a+2b=f(a+b) 所以f(x)f(x)支持加法运算。

因此 f(x)f(x) 是支持线性空间运算。

例证明f(x)=x+1f(x)=x+1不是线性空间。 证明：取a,ba,b 带入 f(x)=x+1f(x)=x+1 f(a)=a+1f(a)=a+1 f(b)=b+1f(b)=b+1 所以f(a)+f(b)=a+b+2f(a)+f(b)=a+b+2 而f(a+b)=a+b+1f(a+b)=a+b+1 这说明f(a+b)≠f(a)+f(b)f(a+b) \ne f(a)+f(b) 所以，他不是线性空间运算。

从初中一次函数图像可以看到f(x)=x+1f(x)=x+1 之所以不支持线性运算最根本元素是图形不过原点。

线性变换

一旦我们掌握了线性变换，就可以向高纬度推广， 例如要得到函数 f(x1,x2)=k1x1+k2x2f\left(x_1, x_2\right)=k_1 x_1+k_2 x_2 的图形, 只要把三维坐标系下的两个函数 f(x1,x2)=k1x1f\left(x_1, x_2\right)=k_1 x_1 和 f(x1,x2)=k2x2f\left(x_1, x_2\right)=k_2 x_2 所对应的图形加起来即可。一般情形下, 两个平面相加仍然是一个平面, 如图 1-5 所示。 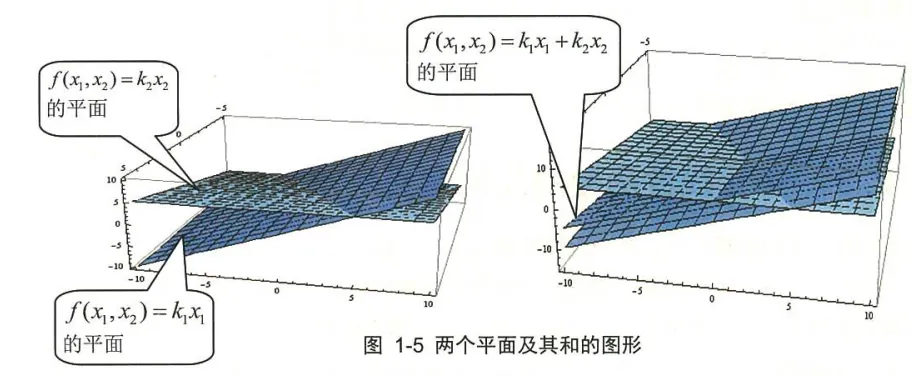图片 因此, 线性函数 f(x1,x2)=k1x1+k2x2f\left(x_1, x_2\right)=k_1 x_1+k_2 x_2 的几何图形是一个过原点的平面。这个平面是在三维坐标系下的二维几何图形。详见 线性空间的推广

Previous2._向量的概念及运算
Next4._方程的向量表示及线性组合