4.4 低秩适配方法

低维固有维度假设[1]表明：过参数化模型的固有维度是很低的；换言之，存在可以与全参数更新媲美的低维的参数更新。基于这一假设，低秩适配方法（Low-rank Adaptation Methods）通过低秩矩阵来近似原始权重更新矩阵，并仅微调低秩矩阵，以大幅降低模型参数量。在本节中，我们首先将介绍最经典的低秩适配方法LoRA的实现细节并对分析其参数效率。接着，将介绍LoRA的相关变体。最后，介绍基于LoRA插件化特性，以及其任务泛化能力。

图4.8: LoRA示意图。

4.4.1 LoRA

低秩适配（Low-rank Adaptation, LoRA）[19]提出利用低秩矩阵近似参数更新矩阵来实现低秩适配。该方法将参数更新矩阵低秩分解为两个小矩阵。在微调时，通过微调这两个小矩阵来对大语言模型进行更新，大幅节省了微调时的内存开销。本小节首先介绍LoRA方法的具体实现过程，然后分析其计算效率。

1. 方法实现

给定一个密集神经网络层, 其参数矩阵为 $W_0 \in \mathbb{R}^{d \times k}$ , 为适配下游任务, 我们通常需要学习参数更新矩阵 $\Delta W \in \mathbb{R}^{d \times k}$ , 对原始参数矩阵进行更新 $W = W_0 + \Delta W$ 。对于全量微调过程, $\Delta W$ 是需对该层所有 $d \times k$ 个参数计算梯度, 这通常需要大量的 GPU 内存, 成本高昂。为解决这一问题, 如图 4.8, LoRA 将 $\Delta W$ 分解为两个低参数量的矩阵 $B \in \mathbb{R}^{d \times r}$ 和 $A \in \mathbb{R}^{r \times k}$ , 使得更新过程变为:

W = W _ {0} + \alpha B A, \tag {4.9}

其中，秩 $r \ll \min\{d, k\}$ ， $B$ 和 $A$ 分别用随机高斯分布和零进行初始化， $\alpha$ 是缩放

因子，用于控制 LoRA 权重的大小。在训练过程中，固定预训练模型的参数，仅微调 $B$ 和 $A$ 的参数。因此，在训练时，LoRA 涉及的更新参数数量为 $r \times (d + k)$ ，远小于全量微调 $d \times k$ 。实际上，对于基于 Transformer 的大语言模型，密集层通常有两种类型：注意力模块中的投影层和前馈神经网络（FFN）模块中的投影层。在原始研究中，LoRA 被应用于注意力层的权重矩阵。后续工作表明将其应用于 FFN 层可以进一步提高模型性能 [14]。

LoRA仅微调部分低秩参数，因此具有很高的参数效率，同时不会增加推理延迟[10]。此外，低秩矩阵还可以扩展为低秩张量[3]，或与Kronecker分解结合使用，以进一步提高参数效率[9,16]。除了参数效率外，在训练后可以将LoRA参数与模型参数分离，所以LoRA还具有可插拔性。LoRA的可插拔特性使其能够封装为被多个用户共享和重复使用[38]的插件。当我们有多个任务的LoRA插件时，可以将这些插件组合在一起，以获得良好的跨任务泛化性能[20]。我们将在4.4.3提供具体案例详细介绍基于LoRA插件的任务泛化。

2. 参数效率

下面我们以一个具体的案例分析 LoRA 的参数效率。在 LLaMA2-7B [40] 模型中微调第一个 FFN 层的权重矩阵为例，全量微调需要调整 $11,008 \times 4,096 = 45,088,768$ 个参数。而当 $r = 4$ 时，LoRA 只需调整 $(11,008 \times 4) + (4 \times 4,096) = 60,416$ 个参数。对于这一层，与全量微调相比，LoRA 微调的参数不到原始参数量的千分之一。具体来说，模型微调的内存使用主要涉及四个部分：

权重内存（Weight Memory）：用于存储模型权重所需的内存；
激活内存（Activation Memory）：前向传播内存时中间激活带来的显存占用，主要取决于 batch size 大小以及序列长度等；
梯度内存 (Gradient Memory): 在反向传播期间需要用来保存梯度的内存, 这些梯度仅针对可训练参数进行计算;
优化器内存（Optimization Memory）：用于保存优化器状态的内部存在。例如，Adam 优化器会保存可训练参数的“一阶动量”和“二阶动量”。

文献[34]提供在LLaMA2-7B模型上使用批量大小为1,单个NVIDIA RTX4090(24GB）GPU上进行全量微调和LoRA微调的实验对比。根据实验结果，全量微调大约需要60GB显存，超出RTX4090的显存容量。相比之下，LoRA只需要大约23GB显存。LoRA显著减少了显存使用，使得在单个NVIDIA RTX4090上进行LLaMA2-7B微调成为可能。具体来说，由于可训练参数较少，优化器内存和梯度内存分别减少了约25GB和14GB。另外，虽然LoRA引入了额外的“增量参数”，导致激活内存和权重内存略微增加（总计约2GB)，但考虑到整体内存的减少，这种增加是可以忽略不计的。此外，减少涉及到的参数计算可以加速反向传播。与全量微调相比，LoRA的速度提高了1.9倍。

4.4.2 LoRA相关变体

虽然 LoRA 在一些下游任务上能够实现较好的性能，但在许多复杂的下游任务（如数学推理 [4,6,54]）上，LoRA 与全量微调之间仍存在性能差距。为弥补这一差距，许多 LoRA 变体方法被提出，以进一步提升 LoRA 在下游任务中的适配性能。现有方法主要从以下几个角度进行改进 [31]: (1) 打破低秩瓶颈；(2) 动态秩分配；(3) 训练过程优化。接下来，将分别介绍这三种类型变种的代表性方法。

1.打破低秩瓶颈

LoRA的低秩更新特性使其在参数效率上具有优势；然而，这也限制了大规模语言模型记忆新知识和适应下游任务的能力[4,13,21,54]，即存在低秩瓶颈。Biderman等人[4]的实验研究表明，全量微调的秩显著高于LoRA的秩（10-100倍），并且增加LoRA的秩可以缩小LoRA与全量微调之间的性能差距。因此，一些方法被提出，旨在打破低秩瓶颈[25,36,48]。

例如，ReLoRA [25] 提出了一种合并和重置（merge-and-reinit）的方法，该方法在微调过程中周期性地将 LoRA 模块合并到大语言模型中，并在合并后重新初始化 LoRA 模块和优化器状态。具体地，合并的过程如下：

W ^ {i} \leftarrow W ^ {i} + \alpha B ^ {i} A ^ {i}, \tag {4.10}

其中， $W^{i}$ 是原始的权重矩阵， $B^{i}$ 和 $A^{i}$ 是低秩分解得到的矩阵， $\alpha$ 是缩放因子。合并后，将重置 $B^{i}$ 和 $A^{i}$ 的值重置，通常 $B^{i}$ 会使用特定的初始化方法（如Kaiming初始化）重新初始化，而 $A^{i}$ 则被设置为零。为了防止在重置后模型性能发散，ReLoRA还会通过幅度剪枝对优化器状态进行部分重置。合并和重置的过程允许模型在保持总参数量不变的情况下，通过多次低秩LoRA更新累积成高秩状态，从而使得ReLoRA能够训练出性能接近全秩训练的模型。

2.动态秩分配

然而，LoRA的秩并不总是越高越好，冗余的LoRA秩可能会导致性能和效率的退化。并且，微调时权重的重要性可能会因Transformer模型中不同层而存在差异，因此需要为每个层分配不同的秩[7,30,41,52]。

例如，AdaLoRA [52] 通过将参数更新矩阵参数化为奇异值分解（SVD）的形式，再通过奇异值剪枝动态调整不同层中 LoRA 模块的秩。具体地，AdaLoRA 使用奇异值分解重新表示 $\Delta W$ ，即

W = W _ {0} + \Delta W = W _ {0} + P \Lambda Q, \tag {4.11}

其中， $P \in \mathbb{R}^{d \times r}$ 和 $Q \in \mathbb{R}^{r \times k}$ 是正交的， $\Lambda$ 是一个对角矩阵，其中包含 $\{\lambda_i\}_{1 \leq i \leq r}$ 的奇异值。在训练过程中， $W_0$ 的参数被固定，仅更新 $P$ 、 $\Lambda$ 和 $Q$ 的参数。根据梯度权重乘积大小的移动平均值构造奇异值的重要性得分，对不重要的奇异值进行迭代剪枝。此外，为了增强稳定训练性，AdaLoRA 引入一个额外的惩罚项确保 $P$

和 $Q$ 之间的正交性：

R (P, Q) = | | P ^ {T} P - I | | _ {F} ^ {2} + | | Q Q ^ {T} - I | | _ {F} ^ {2}, \tag {4.12}

其中， $I$ 是单位矩阵， $\| \cdot \| _F$ 代表Frobenius范数。

3. 训练过程优化

在实际微调过程中，LoRA的收敛速度比全量微调要慢。此外，它还对超参数敏感，并且容易过拟合。这些问题影响了LoRA的效率并阻碍了其下游适配性能。为了解决这些问题，一些工作尝试对LoRA的训练过程进行优化[32,45]。代表性方法DoRA(权重分解低秩适应)[29]提出约束梯度更新，侧重于更新参数的方向变化。它将预训练权重 $W_0\in \mathbb{R}^{d\times k}$ 分解为方向和大小两个组件，并仅将LoRA应用于方向组件以增强训练稳定性。具体地，DoRA将 $W_{0}\in \mathbb{R}^{d\times k}$ 重新表示为：

W _ {0} = m \frac {V}{\| V \| _ {c}} = \| W _ {0} \| _ {c} \frac {W _ {0}}{\| W _ {0} \| _ {c}}, \tag {4.13}

其中， $m \in \mathbb{R}^{1 \times k}$ 是大小向量， $V \in \mathbb{R}^{d \times k}$ 是方向矩阵， $\| \cdot \|_c$ 是矩阵在每一列上的向量范数。随后，DoRA 仅对方向矩阵 $V$ 施加 LoRA 进行参数化，定义为：

W ^ {\prime} = \underline {{m}} \frac {V + \underline {{\Delta V}}}{\| V + \underline {{\Delta V}} \| _ {c}} = \underline {{m}} \frac {W _ {0} + \underline {{B A}}}{\| W _ {0} + \underline {{B A}} \| _ {c}}, \tag {4.14}

其中， $\Delta V$ 是由 LoRA 学习的增量方向更新，下划线参数表示可训练参数。

4.4.3 基于 LoRA 插件的任务泛化

在 LoRA 微调结束后，我们可以将参数更新模块 $B$ 和 $A$ 从模型上分离出来，并封装成参数插件。这些插件具有即插即用、不破坏原始模型参数和结构的优良性质。我们可以在不同任务上训练的各种 LoRA 模块，将这些模块插件化地方式保存、共享与使用。此外，我们还可以将多个任务的 LoRA 插件组合，然后将不同任务的能力迁移到新任务上。LoRAHub [20] 提供了一个可用的多 LoRA 组合的方法框架。其可将已有任务上得到的 LoRA 插件进行组合，从而获得解决新任务的能

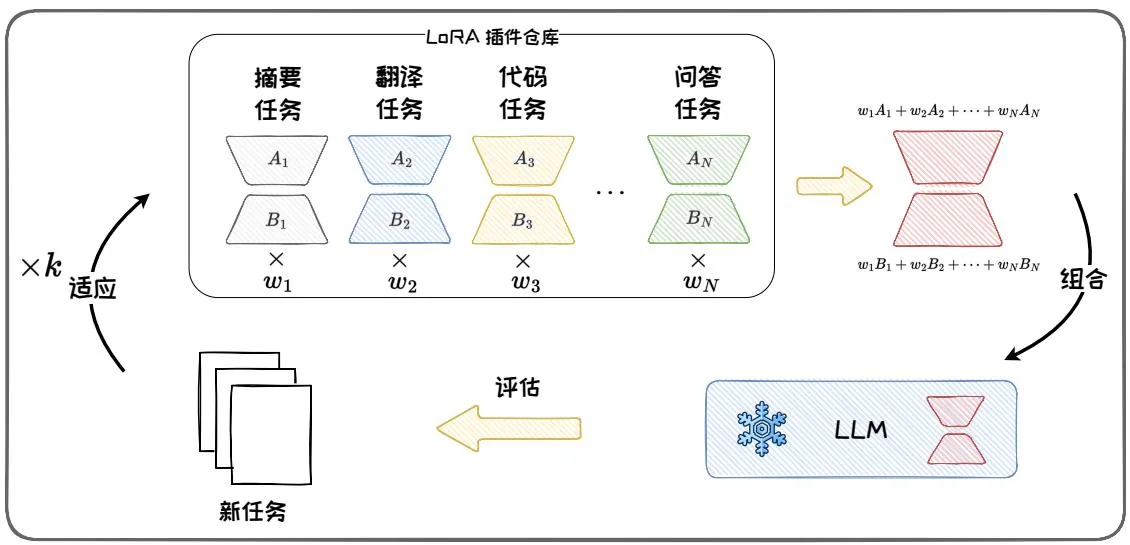
图4.9: LoRAHub示意图。

力。如图 4.9 所示, LoRAHub 包括两个阶段: 组合阶段和适应阶段。在组合阶段, LoRAHub 将已学习的 LoRA 模块通过逐元素线性加权组合为单一模块:

\hat {m} = \left(w _ {1} A _ {1} + w _ {2} A _ {2} + \dots + w _ {N} A _ {N}\right) \left(w _ {1} B _ {1} + w _ {2} B _ {2} + \dots + w _ {N} B _ {N}\right), \tag {4.15}

其中， $w_{i}$ 是第 $i$ 个LoRA模块的权重， $\hat{m}$ 是组合后的模块， $A_{i=1}^{N}$ 和 $B_{i=1}^{N}$ 分别是 $N$ 个LoRA分解矩阵。在适应阶段，给定一些新任务的示例，通过无梯度方法Shiwa[28]自适应地学习权重组合。适应和组合经过 $k$ 次迭代，直至找到最优的权重组合，以完成对新任务的适应。

本节介绍了低秩适配方法 LoRA。LoRA 通过对参数矩阵进行低秩分解，仅训练低秩矩阵，大幅减少了训练参数量。此外，还介绍了从打破低秩瓶颈、动态秩分配和训练过程优化等不同角度改进 LoRA 的变体。最后，介绍了基于 LoRA 插件的任务泛化方法 LoRAHub。LoRAHub 通过对已学习的 LoRA 模块加权组合，融合多任务能力并迁移到新任务上，提供了一种高效的跨任务学习范式。

4.4_低秩适配方法