13.2 Overview

A simple implementation in $\mathbb{C} + +$ looks like Listing 13.1.

Listing 13.1 Inclusive scan (in C++.)

template<class T>  
T InclusiveScan(T *out, const T *in, size_t N)  
{ T sum(0); for (size_t i = 0; i < N; i++) { sum += in[i]; out[i] = sum; } return sum; }

For these serial implementations in Listings 13.1 and 13.2, the only difference between inclusive and exclusive scan is that the lines

out[i] = sum;  
and  
sum += in[i];  
are swapped.1

Listing 13.2 Exclusive scan (in C++.)

template<class T>  
T  
ExclusiveScan(T *out, const T *in, size_t N)  
{  
    T sum(0);  
    for (size_t i = 0; i < N; i++) {  
        out[i] = sum;  
        sum += in[i];  
    }  
    return sum;

The serial implementations of Scan are so obvious and trivial that you are forgiven if you're wondering what a parallel implementation would look like! The so-called prefix dependency, where each output depends on all of the preceding inputs, may have some wondering if it's even possible. But, upon reflection, you can see that the operations for neighboring pairs $\{a_{i} \oplus a_{i+1}$ for $0 \leq i < N-1\}$ could be computed in parallel; for $i = 0$ , $a_{i} \oplus a_{i+1}$ computes a final output of the Scan, and otherwise these pairwise operations compute partial sums that can be used to contribute to the final output, much as we used partial sums in Chapter 12.

Blelloch² describes a two-pass algorithm with an upsweep phase that computes the reduction of the array, storing intermediate results along the way, and followed by a downsweep that computes the final output of the scan. Pseudocode for the upsweep as is follows.

upssweep(a,N)   
for d from 0 to (lg N)-1   
in parallel for i from 0 to N-1 by  $2^{d + 1}$  a[i+2d+1-1] +=a[i+2d-1]

The operation resembles the log-step reduction we have discussed before, except intermediate sums are stored for later use in generating the final output of the scan.

After Blelloch, Figure 13.2 shows an example run of this upsweep algorithm on an 8-element array using addition on integers. The "upsweep" terminology stems from thinking of the array as a balanced tree (Figure 13.3).

Once the upsweep has been completed, a downsweep propagates intermediate sums into the leaves of the tree. Pseudocode for the downsweep is as follows.

Step

Figure 13.2 Upsweep pass (array view).

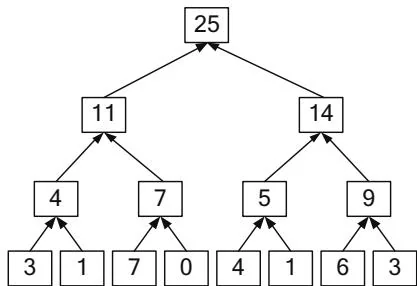
Figure 13.3 Upsweep pass (tree view).

downsweep(a, N)  
a[N-1] = 0  
for d from (lg N)-1 downto 0  
in parallel for i from 0 to N-1 by  $2^{d+1}$   
t := a[i+2^d-1]  
a[i+2^d-1] = a[i + 2^{d+1} - 1]  
a[i+2^{d+1} - 1] += t

Figure 13.4 shows how the example array is transformed during the downsweep, and Figure 13.5 shows the downsweep in tree form. Early implementations of Scan for CUDA followed this algorithm closely, and it does make a good introduction to thinking about possible parallel implementations. Unfortunately, it is not a great match to CUDA's architecture; a naive implementation suffers from shared memory bank conflicts, and addressing schemes to compensate for the bank conflicts incurs enough overhead that the costs outweigh the benefits.

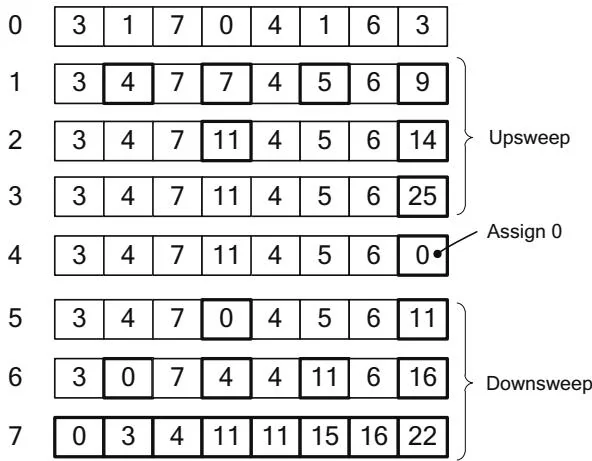
Step
Figure 13.4 Downsweep (array view).

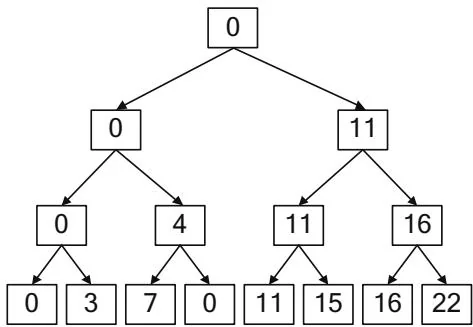
Figure 13.5 Downsweep (tree view).

13.2_Overview

13.2 Overview

Step