在实际问题当中,对正态分布的均值和方程估计非常常见,依据 μ,σ2 的不同,主要分为四种情况,下面分布介绍。
(1)σ2 已知,均值 μ 的置信区间
证明 设 X1,X2,⋯,Xn 是来自总体 X∼N(μ,σ2),σ2 为已知,μ 为末知的样本,求置信概率为 1−α 的 μ 的置信区间。
解: 由 X1,X2,⋯,Xn 来自总体 X∼N(μ,σ2) 的样本及 Xˉ 是 μ 的无偏估计可知,
u=σ/nXˉ−μ∼N(0,1) 由标准正态分布分位点 uα/2 的定义,有
P{σ/nXˉ−μ<uα/2}=1−α 即
P{Xˉ−nσuα/2<μ<Xˉ+nσuα/2}=1−α 所以置信概率为 1−α 的 μ 的置信区间为
[Xˉ−u2αnσ,Xˉ+u2αnσ]. 常写成 (Xˉ±nσuα/2) .
上面的证明过于抽象,下面例题反应他的实际意义。
例 新疆旅游局为调查新疆旅游者的平均消费额,随机访问了 100 名旅游者,得知平均消费额 xˉ=80 元。根据经验,已知旅游者消费服从正态分布,且标准差 σ=12 元,求该地旅游者平均消费额 μ 的置信度为 95% 的置信区间.
分析:本题要求估算旅游者平均消费额多少钱,现在已经知道平均消费80元,这是一个点估计,本题要求给出的是区间估计,结合本题稍后给出的答案,本题可以转换为:我有95%的把握说用户的平均消费金额在77.6∼82.4
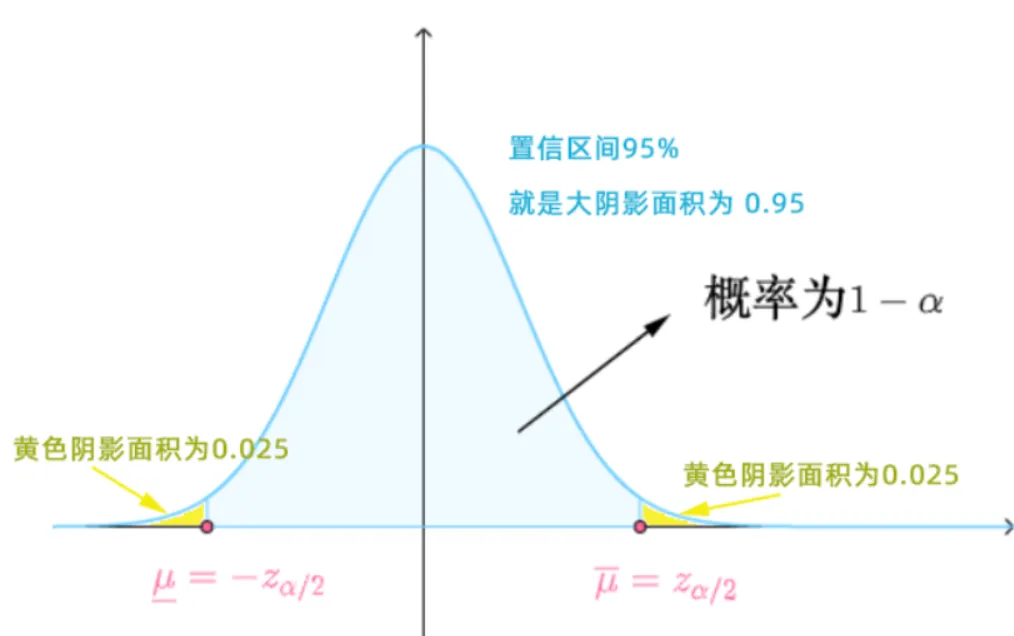
95% 的置信区间就是要求所估计的平均消费金额有95%可能性在下图大的阴影面积里。
 {width=500px}
{width=500px}
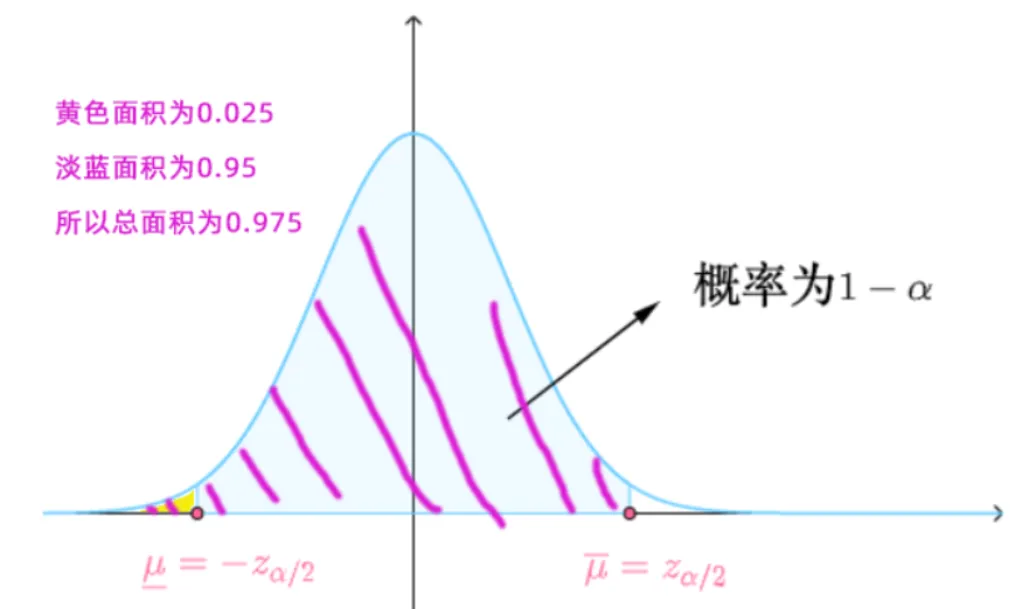
因为考试时正态分布表不会给你数据直接查,所以需要进行转换。换句话说两旁的黄色面积总和为0.05, 考虑标准正态分布的对称性直接把α除以2, 所以两侧黄色阴影的面积各为2α=0.025
由此可得斜线阴影面积为 0.025+0.95=0.975
 {width=500px}
{width=500px}
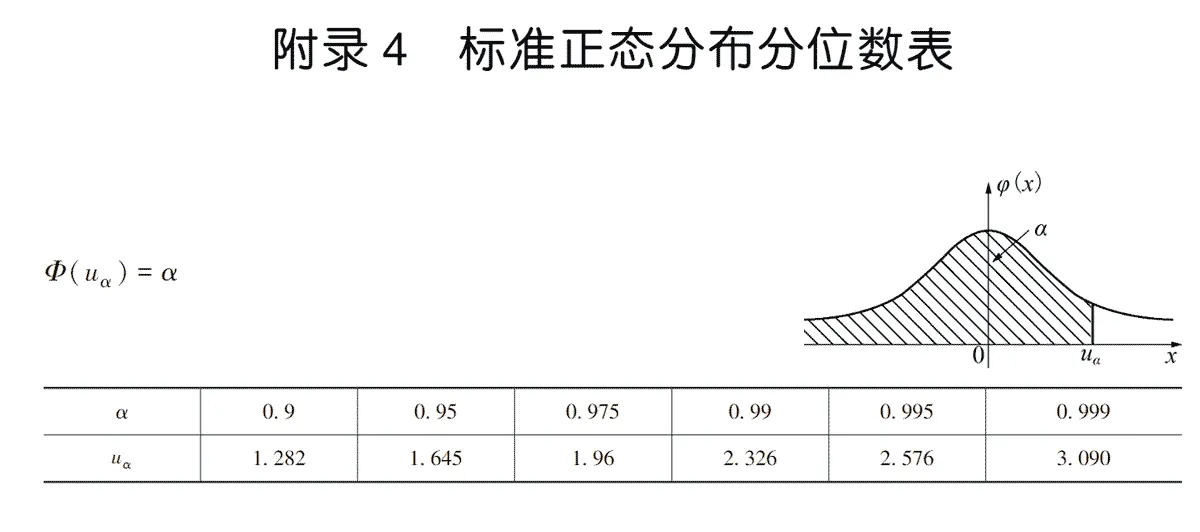
下面把视角切换到正态分布表里。 从正态分布分位数表可以看到当ua=1.96 时,阴影面积正好为0.975.
上面这个结论最好记住:当正态分布估计量上下浮动±1.96时,此时具有 95% 的可信度,这是一个常用的结论
 {width=600px}
{width=600px}
解:
对于给定的置信度
1−α=0.95 可知
α=0.05,α/2=0.025 查标准正态分布表得
附录给出了 标准正态分布分位表
u0.025=1.96 由
n=100,xˉ=80,σ=12,u0.025=1.96 计算得
xˉ−uα/2⋅nσ=80−1.96∗1012=82.4=77.6,xˉ+uα/2⋅nσ=80+1.96∗1012=82.4, 所以 μ 的置信度为 95% 的置信区间为 (77.6,82.4) ,
即在已知误差为 σ=12 的情形下,可以 95% 的置信度认为每个旅游者的平均消费额在 77.6∼82.4 元范围内.
扩展本题
如果本题要求有90%的置信区间呢?此时阴影面积为0.9+0.05=0.95,查表得ua=1.645
计算得
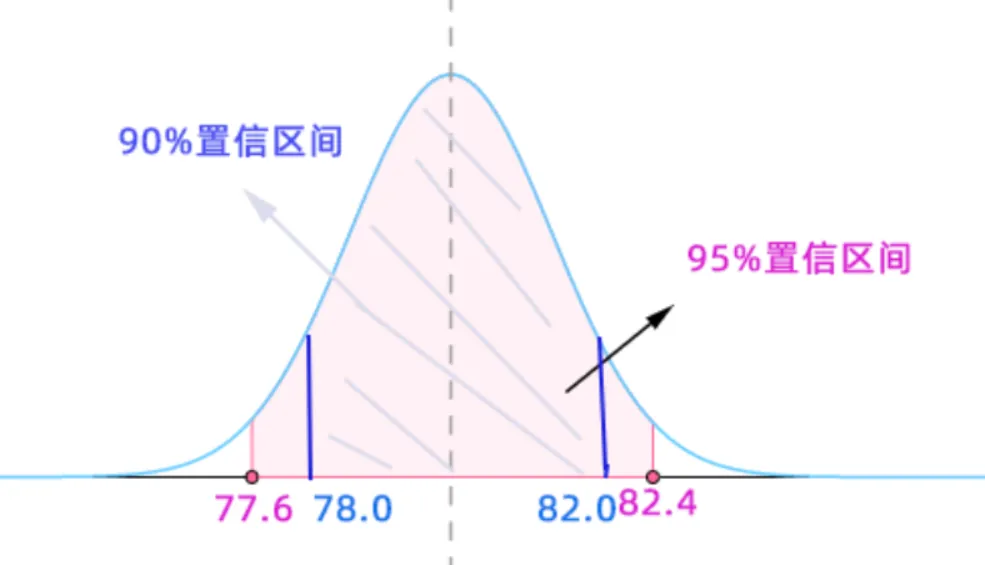
xˉ−uα/2⋅nσ=80−1.645∗1012=82.4=78.0xˉ+uα/2⋅nσ=80+1.645∗1012=82.0 对结果解读:
如果领导问你,游客平均消费多少呀?你可以回答,我有95%的把握说用户消费金额在77.6∼82.4 之间,如果希望更精确的消费答案,我有90%的把握说用户消费金额在 78.0∼82.0之间。从本题还可以看到,因为后者限定的范围更小,导致我在估算时的保证度降低,所以需要理解其中的含义。
 {width=500px}
{width=500px}
例 某工厂生产一种特殊的发动机套筒,假设套筒直径 X(mm) 服从正态分布 N(μ,0.12) ,现从某天的产品中随机抽取 40 件,测得直径的样本均值为 5.426(mm) ,求 μ 的置信度为 0.95 的置信区间.
解 因为 σ2 已知,所以 μ 的置信度为 1−α 的置信区间为
[Xˉ−u2αnσ,Xˉ+u2αnσ]. 由题意得 xˉ=5.426,n=40,σ=0.1,α=0.05 ,查表 得 u2α=u0.025=1.96 .
将上述数据代入公式,得 μ 的置信度为 0.95 的置信区间为
[5.426−1.96×400.1,5.426+1.96×400.1]=[5.395,5.457]. (2)σ2 未知,均值 μ 的置信区间
由于 σ2 末知,故考虑用 σ2 的无偏估计量 S2=n−11∑i=1n(Xi−Xˉ)2 来代替 σ2 ,则得到枢轴量
T=S/nXˉ−μ∼t(n−1) 有
P{−t2α(n−1)⩽T⩽t2α(n−1)}=1−α 即
P{−t2α(n−1)⩽S/nXˉ−μ⩽t2α(n−1)}=1−α 进行恒等变形得
P{Xˉ−t2α(n−1)nS⩽μ⩽Xˉ+t2α(n−1)nS}=1−α 可得 μ 的置信度为 1−α 的置信区间为
[Xˉ−t2α(n−1)nS,Xˉ+t2α(n−1)nS]. 由于
nS=n−1S0,S0=n1i=1∑n(Xi−Xˉ)2 所以 μ 的置信区间也可写成
[Xˉ−n−1S0t2α(n−1),Xˉ+n−1S0t2α(n−1)]. 例 为检查某批零件的长度,随机抽取 16 个零件,测得平均长度为 20.5 cm,样本标准差为 0.8 cm。假设零件长度服从正态分布,求该批零件平均长度 μ 的 95% 置信区间。
解答:
目标:估计总体均值 μ。
条件:总体服从正态分布,但总体方差未知(只给出了样本标准差 S=0.8)。因此,应使用 t 分布。
已知信息:
Xˉ=20.5
S=0.8
n=16
置信水平 1−α=95%,所以 α=0.05。
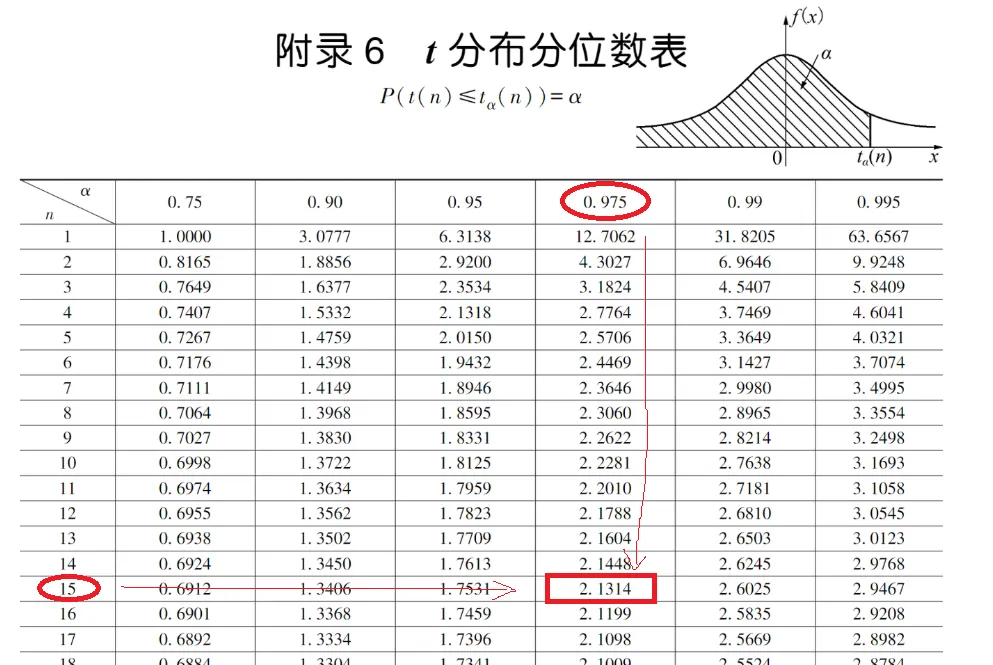
查t分布表:自由度 df=n−1=15,查 t 分布表得 tα/2(15)=t0.025(15)=2.131。
横坐标为什么查0.975和上一个例题原理一样。
纵坐标,自由度为15,这里特别要注意:自由度为n−1,因为在计算方程式,使用了平均值公式,所以减少了一个自由度。
 {width=600px}
{width=600px}
计算误差界,也就是带入上面公式:
E=tα/2(n−1)⋅nS=2.131×160.8=2.131×0.2=0.4262 构建置信区间:
(Xˉ−E, Xˉ+E)=(20.5−0.4262, 20.5+0.4262)=(20.0738, 20.9262) 结论 我们有 95% 的把握认为该批零件的真实平均长度在 20.07 cm 到 20.93 cm 之间。
希望这个详细的总结能帮助你彻底理解单个正态总体的置信区间问题!
在现实生活中,未知方差,估值μ 的置信区间是最经常遇到的。
例 有一大批糖果.现从中随机地取 16 袋,称得重量(以 g 计)如下:
506514508505499493503496504506510502497509512496 设袋装糖果的重量近似地服从正态分布,试求总体均值 μ 的置信水平为 0.95 的置信区间。
解 这里 1−α=0.95,α/2=0.025,n−1=15,t0.025(15)=2.1315 ,由给出的数据算得 xˉ=503.75,s=6.2022 .由上面公式得均值 μ 的一个置信水平为 0.95的置信区间为
(503.75±166.2022×2.1315), 即
(500.4,507.1). 这就是说估计袋装糖果重量的均值在 500.4 g 与 507.1 g 之间,这个估计的可信程度为 95% 。若以此区间内任一值作为 μ 的近似值,其误差不大于 166.2022×2.1315×2=6.61( g) ,这个误差估计的可信程度为 95% .
(3)μ 未知,方差 σ2 的置信区间
由 σ2 的无偏估计为 S2 ,从定理知
σ2n−1S2∼χ2(n−1) 请注意:对于α的处理,我们总是一分为二(不管是不是对称,主要还是为了方便),比如歌手参加比赛,得到10组打分,通常,为了公平我们会去掉1个最高分和1个最低分,剩下的8个取总和(或平均值)作为选手的得分。同样,在概率论里,我们要求 95%可信度,也就是说有5%不可信,这5%的不可信一分为二,前面和后面各占2.5%
由于 χ2 分布是偏态分布,所以将 α 平分为两部分,在 χ2 分布两侧各截面积为 2α 的部分,即采用 χ2 分布的两个分位点 χα/22(n−1) 和 χ1−α/22(n−1) (见图 ).
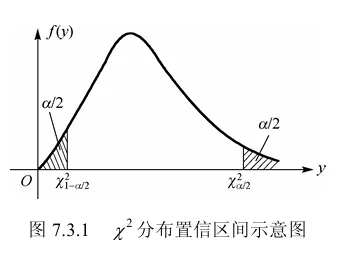
对给定的置信水平 1−α ,有
P{χ1−α/22(n−1)<σ2n−1S2<χα/22(n−1)}=1−α, 即
P{χα/22(n−1)(n−1)S2<σ2<χ1−α/22(n−1)(n−1)S2}=1−α 于是方差 σ2 的 1−α 置信区间为
(χα/22(n−1)(n−1)S2,χ1−α/22(n−1)(n−1)S2) 实际问题中在要考虑精度或稳定性时,需要对正态总体的方差 σ2 进行区间估计,情况下面例题
例 已知某种钢丝的折断力服从正态分布 N(μ,σ2) ,从一批钢丝中任意抽取 10 根,测得折断力数据(单位: kg )如下:
578,572,570,568,572,570,570,596,584,572. 求 σ2 和 σ 的置信度为 0.9 的置信区间.
解:由于 μ 末知,则 σ2 的置信度为 1−α 的置信区间为
[χ2α2(n−1)(n−1)S2,χ1−2α2(n−1)(n−1)S2] 现在带入数据, 均值为 (578+572+570+568+572+570+570+596+584+572)/10=575.2
方差为:
SS=(578−575.2)2+(572−575.2)2+(570−575.2)2+(568−575.2)2+(572−575.2)2+(570−575.2)2+(570−575.2)2+(596−575.2)2+(584−575.2)2+(572−575.2)2=681.60 样本方差公式(无偏估计)s2=n−1SS=9681.60≈75.733
由 n=10 和 α=0.1 ,查表 卡方分布表
注意:需要要查n=9,而不是10. 因为自由度减1才是无偏性估计
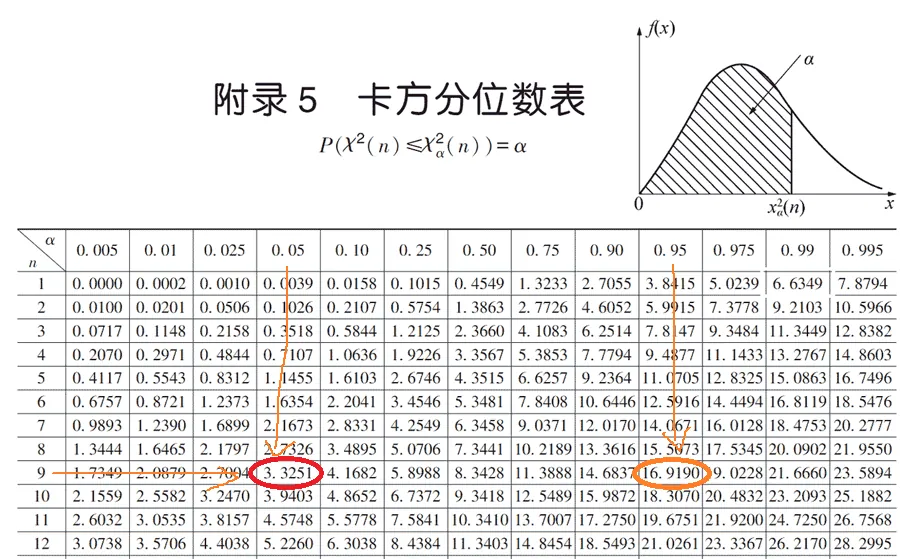
得
χ0.052(9)=16.919,χ0.952(9)=3.325 代入公式即得 σ2 的置信度为 0.9 的置信区间为
[40.28,204.98]
进而得到 σ 的置信度为 0.9 的置信区间为[6.35,14.32] ,本题算出来的样本均值是 575.2,算出来的标准差为6.35和14.32,即 下限浮动为 575.2−6.35=568.8,上限浮动为 575.2+14.32=589.5
结果解读:这个结果的意思是,在这批钢材里,当钢筋受力在 568.8kg∼589.5kg时,我有 90%的把握说,他们会断裂。
(4)μ 已知,方差 σ2 的置信区间
注意:现实中,第(4)种情况是极其少见的,所以基本上不需要掌握,基本上书上也不会介绍
可取枢轴量为
χ2=σ2∑i=1n(Xi−μ)2∼χ2(n) 由
P{χ1−2α2(n)⩽σ2∑i=1n(Xi−μ)2⩽χ2α2(n)}=1−α 可得 σ2 的置信度为 1−α 的置信区间为
[χ2α2(n)∑i=1n(Xi−μ)2,χ1−2α2(n)∑i=1n(Xi−μ)2] 具体推导:略
附录
单侧的置信区间如下表



更详细的附表,请参考 正态总体均值置信区间表
 {width=500px}
{width=500px} {width=500px}
{width=500px} {width=600px}
{width=600px} {width=500px}
{width=500px} {width=600px}
{width=600px}



