枢轴变量的意义
在理解本文前,建议已经看了 置信区间 的介绍
接着上一节,为了估计学生的身高,我测量了50个学生,然后把每个学生的身高描绘出来,这些身高分布呈现正态分布。现在我要使用这50个样本估算全校学生的平均身高,在点估计里,直接使用平均值即可当做总体的平均身高,但是在很多情况下,我们希望获得一个区间,并得到区间的可信度。
参考下图,以95%的可信区间为例,下图阴影部分的面积为0.95,现在样本点已经有了,想象一下,我拿了3把尺子,分别是a1,a2,a3划分区间,在总面积不变的情况下,我希望尺子越短越好,可以证明在左右个为α/2的情况下,尺子最短。
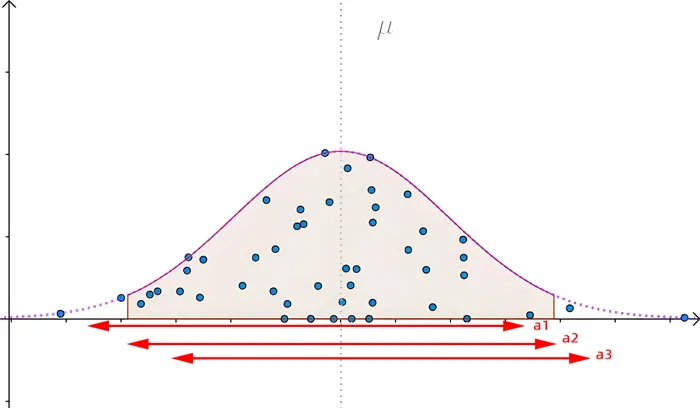
① 如何理解尺子最短?
区间估计要求在保证可信度下,区间尽可能小,这样会更准确。比如我说:我有 95%的把握判断张三的身高为 172-174 和我有 95%的把握判断张三的身高为 160-190, 可以看到,虽然两者置信度一样,但是后面等于没说,就是因为估计的区间太大。
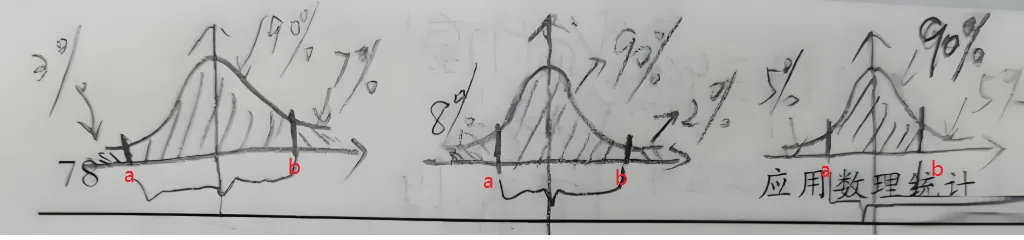
②可以证明,在对称的情况下,尺子最短。参考下图,假设置信区间要求90%的可信度,比如下图左边取 3%,右边取7%, 或者左边取8%,右边取2%,又或者左右两边各取5%。可以证明,只有第三种情况,区间a,b最短,所以使用 α/2
下面视频介绍了上面乘法公式的意义(视频来B站自宋浩《概率论与数理统计》教程)
<video width=600px height="500px"; controls>
枢轴量法求置信区间
构造未知参数 θ 的置信区间的最常用的方法是枢轴量法, 其步骤可以概括为如下三步:
(1) 设法构造一个样本和 θ 的函数 G=G(x1,x2,⋯,xn,θ) 使得 G 的分布不依赖于未知参数.一般称具有这种性质的 G 为枢轴量.
(2) 适当地选择两个常数 c,d, 使对给定的 α(0<α<1), 有
P(c⩽G⩽d)=1−α....(6.6.5) 在离散场合,上式等号改为大于等于( ⩾ )。
(3) 假如能将 c⩽G⩽d 进行不等式等价变形化为 θ^L⩽θ⩽θ^U, 则有
Pθ(θ^L⩽θ⩽θ^U)=1−α,...(6.6.6) 这表明 [θ^L,θ^U] 是 θ 的 1- α 同等置信区间.
上述构造置信区间的关键在于构造枢轴量 G, 故把这种方法称为枢轴量法. 枢轴量的寻找一般从 θ 的点估计出发. 而满足 (6.6.5) 的 c,d 可以有很多, 选择的目的是希望 (6.6.6) 中的平均长度 Eθ(θ^U−θ^L) 尽可能短.
假如可以找到这样的 c,d 使 Eθ(θ^U−θ^L) 达到最短当然是最好的, 不过在不少场合很难做到这一点. 故常这样选择 c 和 d, 使得两个尾部概率各为 α/2, 即
Pθ(G<c)=Pθ(G>d)=α/2, 例题
本例题是上一节 置信区间 例题的进一步分析 ,因此这一节太抽象了,只能靠自己慢慢“悟”吧
例设 X1,X2,⋯,Xn 为来自正态总体 X∼N(μ,σ2) 的样本,其中 σ2 已知, μ 未知,试求出 μ 的置信度为 1−α 的置信区间.
解: 由点估计值,样本均值 Xˉ 是 μ 的良好估计量,且 Xˉ∼N(μ,nσ2) ,故统计量
U=nσXˉ−μ∼N(0,1). 如图6.1所示,根据标准正态分布上 α 分位点的定义,可得
P{−u2α⩽U⩽u2α}=1−α 即
P{−u2α⩽σ/nXˉ−μ⩽u2α}=1−α 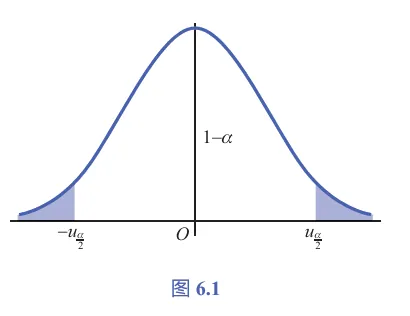
则
P{Xˉ−u2αnσ⩽μ⩽Xˉ+u2αnσ}=1−α 虽然上面推导可能你不太熟悉,但是这个结论需要记住。
由置信区间的定义可知,[Xˉ−u2αnσ,Xˉ+u2αnσ] 即为 μ 的置信度为 1−α 的置信区间.
对此例进行分析,我们发现随机变量 U 在置信区间的构造过程中起着关键作用,它具有下列特点:
(1)是待估参数 μ 和估计量 Xˉ 的函数;
(2)不含其他未知参数;
(3)其分布已知且与未知参数 μ 无关。
我们称满足上述 3 条性质的量 Q 为枢轴量。
在引入枢轴量 Q 的概念后,我们归纳出求置信区间的一般步骤如下:
(1)根据待估参数构造枢轴量 Q ,一般可由未知参数的良好估计量改造得到;
(2)对于给定的置信度 1−α ,利用枢轴量 Q 的分位点确定常数 a 和 b ,使
P{a⩽Q⩽b}=1−α (3)将不等式恒等变形为
P{θ^1⩽θ⩽θ^2}=1−α 即可得到参数 θ 的置信度为 1−α 的置信区间 [θ^1,θ^2] .
例用天平称量某物体的质量 9 次, 得平均值为 xˉ=15.4(g), 已知天平称量结果为正态分布, 其标准差为 0.1(g). 试求该物体质量的 0.95 置信区间.
解:题目说称物体重量服从正态分布,且标准差已经知道了,为 σ=0.1, 因此称重的正态分布就可以写为 X∼(μ,0.12)
其中,μ 为未知数,是我们要估算的。
此处 1−α=0.95,α=0.05, 查表知 u0.975=1.96, 于是该物体质量 μ 的 0.95 置信区间为
xˉ±u1−α/2σ/n=15.4±1.96×0.1/9=15.4±0.0653, 从而该物体质量的 0.95 置信区间为 [ 15.3347,15.4653].
例假设轮胎的寿命服从正态分布. 为估计某种轮胎的平均寿命, 现随机地抽 12 只轮胎试用, 测得它们的寿命 (单位: 万千米) 如下:
\begin{array}
4.68 & 4.85 & 4.32 & 4.85 & 4.61 & 5.02 \\
5.20 & 4.60 & 4.58 & 4.72 & 4.38 & 4.70
\end{array}
试求平均寿命的 0.95 置信区间.
解 此处正态总体标准差未知,可使用 t 分布求均值的置信区间. 本例中经计算有 xˉ=4.7092,s2=0.0615. 取 α=0.05, 查表知 t0.975(11)=2.2010, 于是平均寿命的 0.95 置信区间为
4.7092±2.2010⋅0.0615/12=[4.5516,4.8668]. 在实际问题中, 由于轮胎的寿命越长越好, 因此可以只求平均寿命的置信下限, 也即构造单侧的置信下限。由于
P(sn(xˉ−μ)<t1−α(n−1))=1−α. 由不等式变形可知 μ 的 1−α 置信下限为 xˉ−t1−α(n−1)s/n. 将 t0.95(11)=1.7959 代人计算可得平均寿命 μ 的 0.95 置信下限为 4.5806 (万千米).
枢轴量和统计量的区别:
(1)枢轴量是样本和待估参数的函数,其分布不依赖于任何未知参数;
(2)统计量只是样本的函数,其分布常依赖于未知参数.
例总体 X∼N(μ,σ2),μ,σ2 是未知参数.要估计参数 μ 。设 X1,…,Xn 是一样本,请问下面三个量,
Xˉ,σ/nXˉ−μ,S/nXˉ−μ 哪些是统计量?哪些是枢轴量?
解:(1)只有 Xˉ 是统计量,另两个含有未知参数.所以不是统计量.
(2) Xˉ∼N(μ,σ2/n) ,分布含有未知参数.
σ/nXˉ−μ 含有除了 μ 以外的其他未知参数 σ .
S/nXˉ−μ 只是 μ 和样本的函数,服从 t(n−1) 分布.
所以只有 S/nXˉ−μ 是枢轴量.
例 《微积分》考试结束后,随机选出 100 名学生,计算得他们的平均成绩为 72.3 分,标准差为 15.8 分.假设全部学生的成绩 X∼N(μ,σ2),μ,σ 均未知,求 μ 的置信水平为 95% 的双侧置信区间.
解:解:对于正态总体 X∼N(μ,σ2),X1,…,Xn 是 X 的样本 μ 的极大似然估计是 Xˉ ,
Xˉ∼N(μ,nσ2),⇒σ/nXˉ−μ∼N(0,1) 由于 σ 未知,不能取 σ/nXˉ−μ 作为枢轴量!
S/nXˉ−μ∼t(n−1) ,可以取 S/nXˉ−μ 作为枢轴量
求 a,b ,使得 P(a<S/nXˉ−μ<b)=95% ,且置信区间最短!
即: Xˉ−bnS<μ<Xˉ−anS,⇐a<S/nXˉ−μ<b且 E(Xˉ−anS)−E(Xˉ−bnS)=(b−a)nE(S)=min
等价于在 P(a<S/nXˉ−μ<b)=95% 成立的 a,b 中 b−a=min!注意到 t 分布的对称性,所以
b=−a=t0.025(99)≈z0.025=1.96 由 xˉ=72.3,s=15.8 计算得,μ 的置信水平为 95%的双侧置信区间为(69.2,75.4).
这一置信区间有 95% 的把握包含真值.


