21._连续型_贝塔Beta分布
贝塔分布是统计人员常用的一种数据建模方式,和其它建模不同,他是对概率进行建模。比如盒子里有8个白球2个黑球,前面讨论都是对取得白球数量进行建模,而贝塔分布是对取得白球的概率进行建模
贝塔分布
设 .如果随机变量 服从下列的密度函数,则我们称呼随机变量服从参数为 和 的贝塔分布。
贝塔Beta分布的密度函数如下,我们记作 .
Beta分布的密度函数图像如下
{width=400px}
Beta 应用分布
Beta分布是一个概率的概率分布。它是一种通用的概率分布,可用于对不同场景中的概率进行建模:
广告的点击率的分布;
网站上购买的客户的转化率;
读者为您的博客点赞的可能性;
特朗普赢得一次竞选的可能性;
乳腺癌女性的 5 年生存机会;
由于 Beta 分布对概率进行建模,因此定义域的边界介于 和 之间。
解析贝塔分布
为了掌握 Beta 分布的底层逻辑,我们首先检查一下它的概率密度函数(PDF):
其中:
是 gamma函数
有什么直觉? 让我们先暂时忽略系数 ,只看分子 ,因为 只是使该函数积分为 1 的规格化常数。
上面这句话是什么意思呢?因为密度函数的积分是分布函数,其值必须为1,为了最终积分结果为1,我们会人为增加一些“系数”平衡方程,比如正态分布里含有分母 ,因此不要被Beta分布的复杂公式吓到。
仔细看Beta分母的分子项: 的幂乘以 的幂看起来很熟悉。 我们以前看过,似曾相识的感觉,是!二项式分布
我们从二项式分布的视角来看贝塔时,就容易理解了。

二项式分布和 beta 分布之间的区别在于,前者对成功次数 进行建模,而后者对成功概率进行建模。换句话说,概率是二项式的一个参数;在Beta中,概率是一个随机变量。
理解上面这句话后,再看Beta分布的参数,其中要求 ,这是因为密度的取值范围就是0到1.
理解贝塔分布里的
从二项式分布联想到,你能想到 作为成功的次数和 作为失败的次数,就像二项式分布中的 和 。
-代表成功的次数,类似于二项分布中的 项。 -代表失败的次数,类似于二项分布中的 项。
您可以按照自己的想法选择 和 参数。例如,如果您认为成功的概率非常高(如 ),则可以将 设为 90 ,将 设为 10 。反之,如果您认为失败的概率较高,则应将 设为 设为 10 。
您可以按照自己的想法选择 和 参数。例如,如果您认为成功的概率非常高(如 ),则可以将 设为 90 ,将 设为 10 。反之,如果您认为失败的概率较高,则应将 设为 设为 10 。
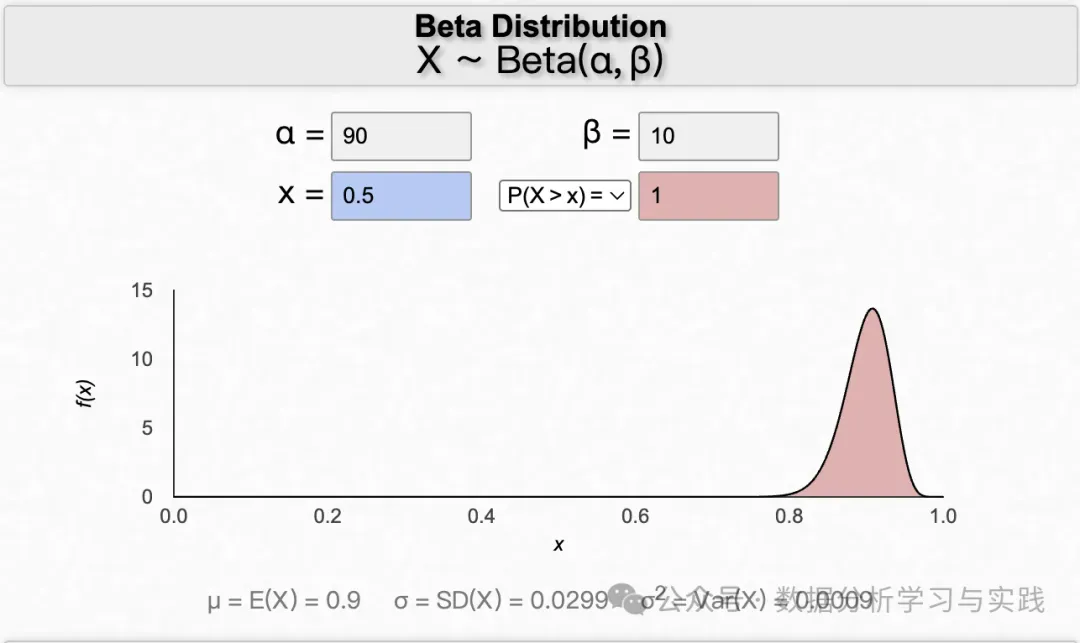
随着 的增加(成功事件增多),概率分布的大部分将向右移动。另一方面, 的增加会使分布向左移动(更多失败事件)。
同样,如果我们同时确定 和 都增加,则分布将变窄。
例子:概率的概率
假设某人同意与你约会的可能性服从 Beta 分布, 。 使用 Beta 分布,您的成功率大于 的概率是多少?用数学术语来说,我们想找到 。
计算 ,我们得到的概率是 0.01953 。不幸的是,这意味着成功率大于 的可能性很低。
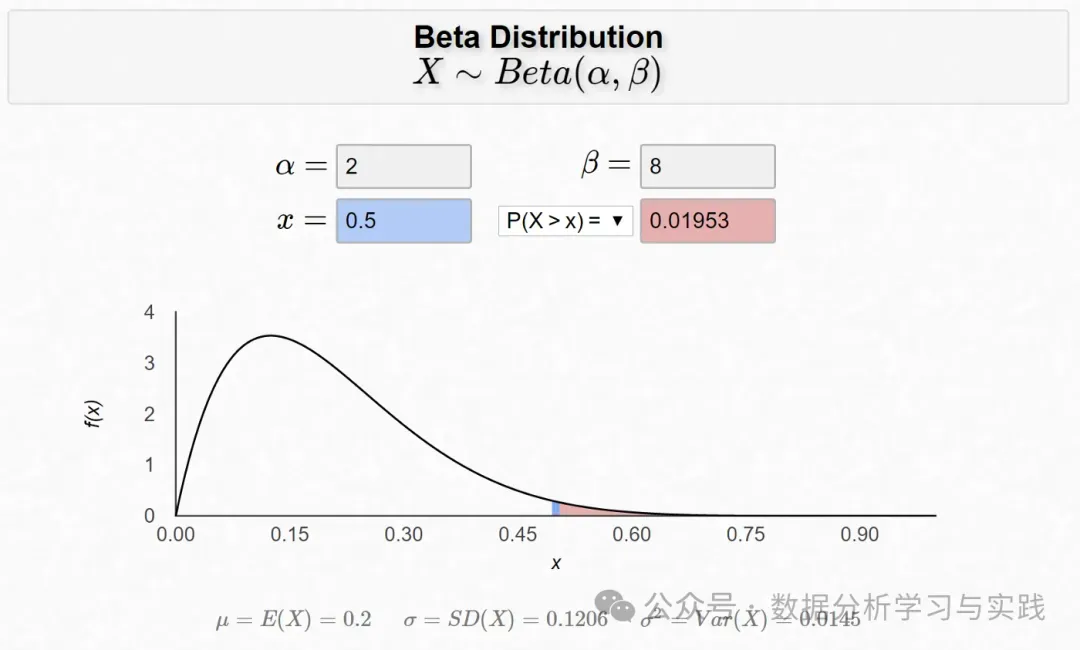
我们为什么使用Beta分布?
说到概率分布建模,有很多选项可供选择。你可能会问,为什么我们要使用 Beta 分布,而不是其他任意的概率分布呢?
如果我们只想创建一个概率分布来模拟概率,我们可以使用区间 上的任意分布。创建一个分布应该很容易。只需使用任何在 0 到 1 之间不会无穷大且保持正值的函数,在这个区间( 0到 1)上进行积分,然后简单地用积分的结果除以该函数。这样就得到了一个概率分布,可以用来建立概率模型。这很有道理,听起来也很简单,但为什么我们坚持使用贝塔分布而不是任意概率分布呢?
Beta分布有何特别之处?
Beta分布是贝叶斯推断中伯努利,二项式,负二项式和几何分布(似乎是涉及成功与失败的分布)的共轭先验,在计算能力不足的情况下,共轭函数对于贝叶斯派来说简直就是救命稻草,而且如此的简单和优雅,像是被上帝亲过一样。
在贝叶斯推理中使用共轭先验(如贝塔分布)具有很大的优势。主要优势之一是使用共轭先验计算后验非常简单。它让我们避免了贝叶斯推断中通常涉及的庞大计算量的数值计算。使用共轭先验时,后验分布与先验分布属于同一族,这大大简化了计算。
如果您不知道共轭先验或贝叶斯推断是什么? 请先理解: 1.作为数据/ML科学家,您的模型永远都不完整。随着输入更多数据,您必须更新模型,这就是我们使用贝叶斯推理的原因。
2.贝叶斯推断中的计算可能非常繁重,有时甚至难以处理。但是,如果我们可以将先验形式的共轭形式使用封闭式公式,那么计算就很容易了。
作为一名数据科学家或机器学习工程师,只要模型还在生产中使用,它就永远不会完成。随着更多数据的到来,你必须更新或重新训练你的模型。这就是我们使用贝叶斯推理的原因。贝叶斯推理的计算量可能会非常大,有时甚至难以实现。但如果我们能使用共轭先验的闭式公式,计算就会变得易如反掌。
在我们的约会例子中,Beta 分布是二项式似然的共轭先验。在建模阶段,如果我们选择使用 Beta 分布作为先验,我们就已经知道后验也将是贝塔分布。因此,在做了更多的实验后(比如请更多的人和你约会),只需将接受和拒绝的次数分别加到现有的参数 上,就可以计算出后验,而不用那么麻烦的用似然乘以先验分布。
总之,贝塔分布是一种方便且可解释的概率模型。它还通过与常见概率分布的共轭关系简化了贝叶斯推断。
Beta分布非常灵活
beta 分布是一种概率分布,可以有多种不同的形状。根据参数 和 的取值,Beta 分布的概率密度函数可以是钟形、有渐近端点的 U 形、严格递增或递减线,甚至是一条水平直线。
a.钟形
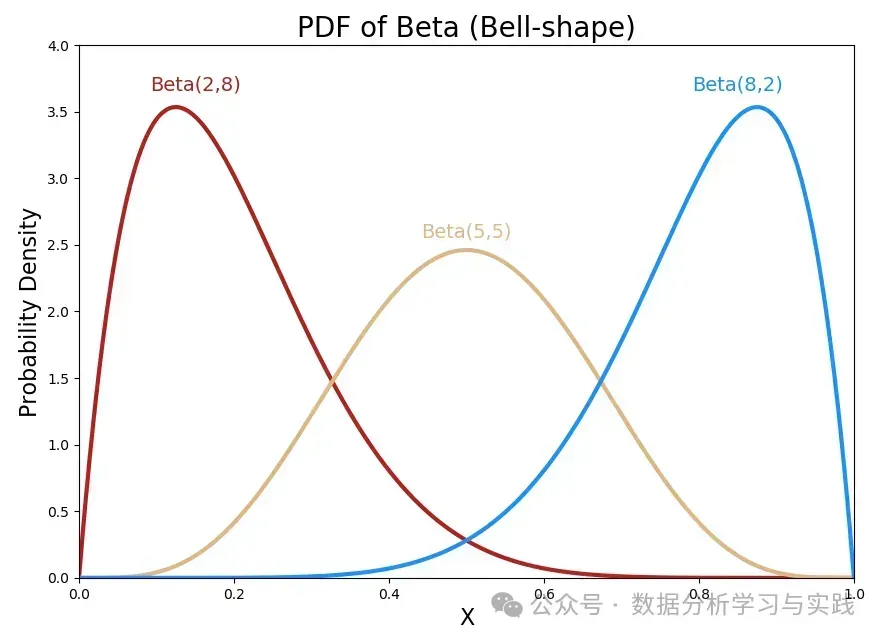
例如,当 和 时,Beta 分布的 PDF 会产生一条蓝色的钟形曲线,而不是红色。 轴代表成功概率。
此外,当 足够大且 和 大致相等时,Beta 分布的PDF可以近似于正态分布。
b.直线
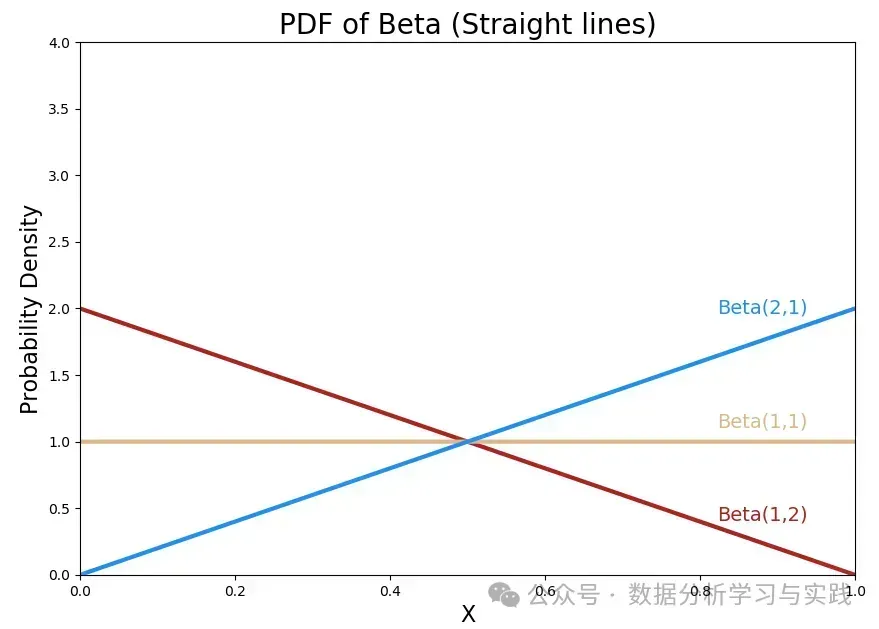 Beta PDF也可以是一条直线!
Beta PDF也可以是一条直线!
c.U形
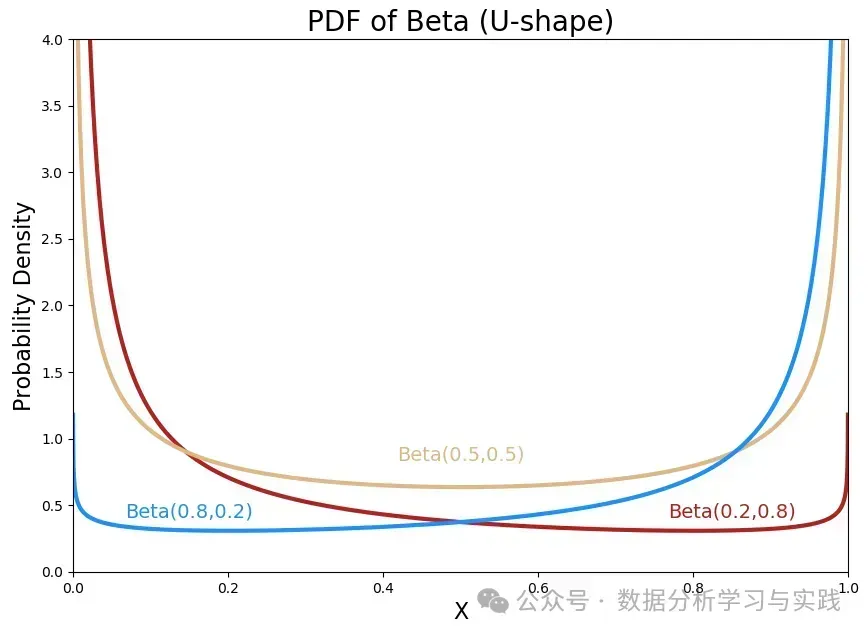
当 和 小于 1 时,分布呈 型,在两端成功的概率最高。
形状的底层逻辑
为什么 是钟形分布? 您可以认为 Beta 分布的形状反映了它所模拟的成功和失败的次数。 例如,如果将 视为成功的次数,将 视为失败的次数, 表示有 1 次成功和 1次失败。因此,成功概率在 0.5 时达到峰值是符合人类认知的。
在这种情况下, 意味着你抛硬币得到了 0 个花面和 0 个 国徽面。那么,您对成功概率的猜测在整个 范围内应该是相同的,正如水平直线所示。
如何理解? 为什么是U型?(-0.5)正面和(-0.5)国徽面是什么意思? 我还没有答案。如果您对U形Beta有个解释,请不吝赐教! 总的来说,beta 分布是一个强大的工具,可用于对各种现象进行建模。 和 参数控制着分布的形状,数值越大,分布越"平滑",数值越小,分布的形状越极端。它的灵活性使其成为数学家、科学家和研究人员的重要工具。
贝塔分布 的数学期望和方差
利用贝塔函数的性质, 不难算得贝塔分布 的数学期望为
方差为
下图给出几种贝塔分布密度函数曲线.
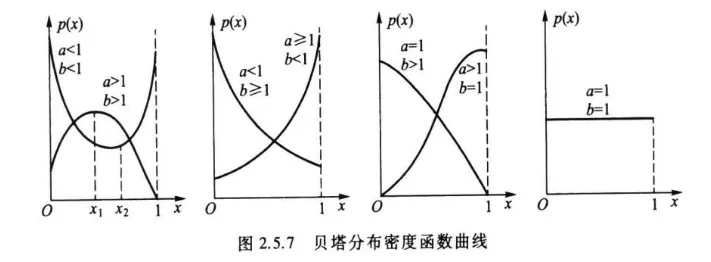
从上图可以看出:
当 时, 是下凸的 形函数.
当 时, 是上凸的单峰函数.
当 时, 是下凸的单调减函数.
当 时, 是下凸的单调增函数.
当 时, .
因为服从贝塔分布 的随机变量是仅在区间 取值的, 所以不合格品率、机器的维修率、市场的占有率、射击的命中率等各种比率选用贝塔分布作为它们的概率分布是恰当的, 只要选择合适的参数 与 即可.
本文部分摘自微信公众号 《数据分析学习与实践》