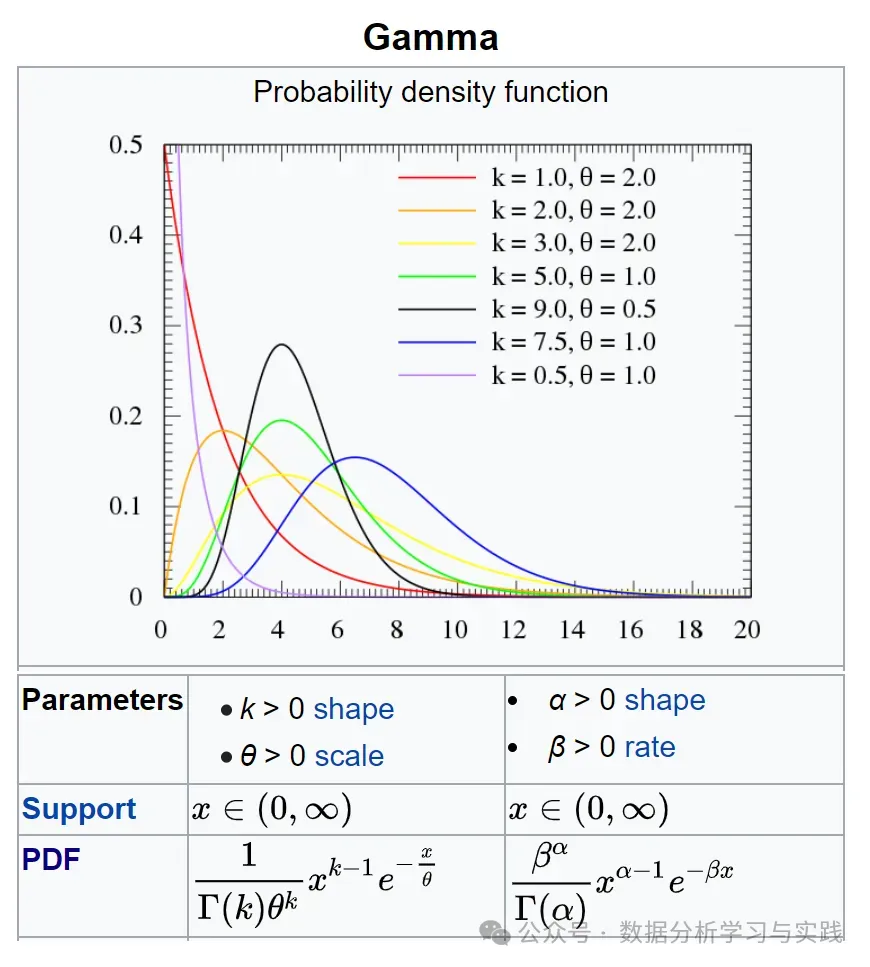
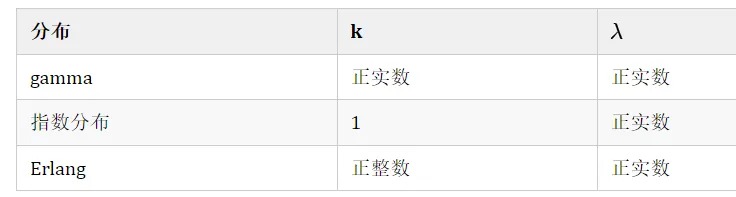
注:在概率论里,和连续分布相关的基本上都和“时间”相关,因为时间是连续的。泊松过程的三个重要分布在概率论和随机过程理论中经常出现,它们分别是:泊松分布 指数分布 伽马分布
伽马分布 若随机变量 X X X
p ( x ) = { λ α Γ ( α ) x α − 1 e − λ x , x ⩾ 0 , 0 , x < 0 , . . . ( 1 ) \boxed{
p(x)= \begin{cases}\dfrac{\lambda^\alpha}{\Gamma(\alpha)} x^{\alpha-1} \mathrm{e}^{-\lambda x}, & x \geqslant 0, \\ 0, & x<0,\end{cases} ...(1)
} p ( x ) = ⎩ ⎨ ⎧ Γ ( α ) λ α x α − 1 e − λ x , 0 , x ⩾ 0 , x < 0 , ... ( 1 ) 则称 X X X X ∼ G a ( α , λ ) X \sim G a(\alpha, \lambda) X ∼ G a ( α , λ ) α > 0 \alpha>0 α > 0 λ > 0 \lambda>0 λ > 0 Γ ( α ) \Gamma(\alpha) Γ ( α )
Γ ( α ) = ∫ 0 ∞ x α − 1 e − x d x \Gamma(\alpha)=\int_0^{\infty} x^{\alpha-1} \mathrm{e}^{-x} \mathrm{~d} x Γ ( α ) = ∫ 0 ∞ x α − 1 e − x d x 对于初次接触伽玛分布的同学,可能会被伽玛分布的密度函数吓跑,感觉太复杂了,请注意:正像正态分布里有2 π \sqrt{2 \pi} 2 π Γ ( α ) \Gamma(\alpha) Γ ( α )
为了方便后面的讲解,这里给出伽玛分布的第二种写法,仅需要简单的变量替换即可, 如果令(1)中 λ = 1 θ \lambda=\frac{1}{\theta} λ = θ 1
p ( x ) = { 1 Γ ( α ) θ α x α − 1 e − x θ , x ⩾ 0 , 0 , x < 0 , . . . ( 2 ) \boxed{
p(x)= \begin{cases}\dfrac{1}{\Gamma(\alpha) \theta^{\alpha}} x^{\alpha-1} e^{-\frac{x}{\theta}}, & x \geqslant 0, \\ 0, & x<0,\end{cases} ...(2)
} p ( x ) = ⎩ ⎨ ⎧ Γ ( α ) θ α 1 x α − 1 e − θ x , 0 , x ⩾ 0 , x < 0 , ... ( 2 ) 在这个写法里,λ \lambda λ 1 7 \frac{1}{7} 7 1 ( λ ) (\lambda) ( λ ) 1 / 3 1 / 3 1/3 ( 1 / λ ) (1 / \lambda) ( 1/ λ ) 泊松分布 里的解释。
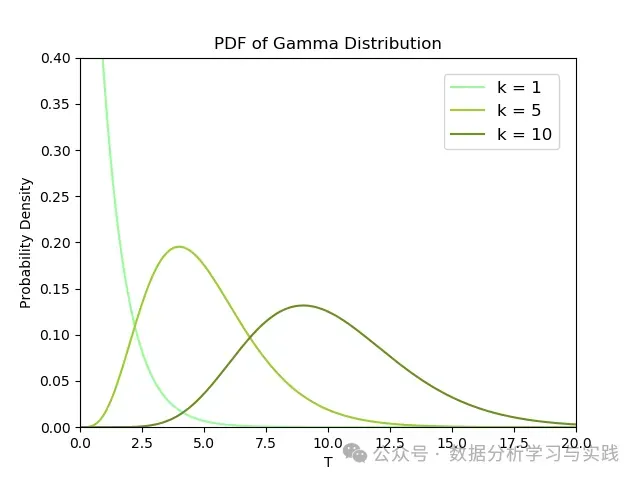
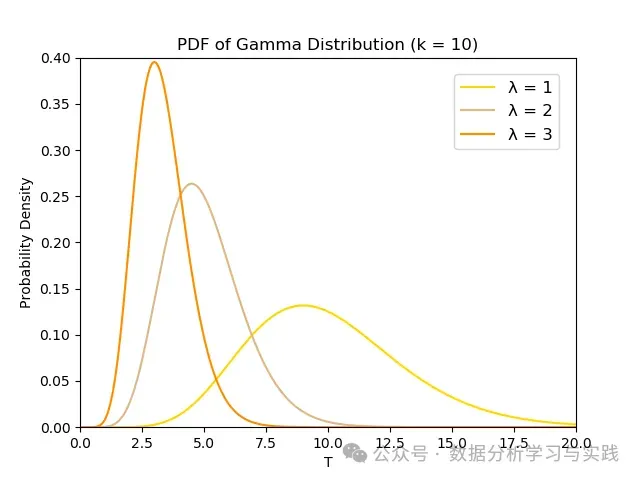
伽马分布的密度函数图像 关于对密度函数的理解,参考本文后半部。
伽玛函数 在理解伽玛分布前,先介绍一下伽玛函数,顾名思义,看到伽玛分布,他一定和伽玛函数有光,伽玛函数的定义是:
Γ ( α ) = ∫ 0 ∞ x α − 1 e − x d x \Gamma(\alpha)=\int_0^{\infty} x^{\alpha-1} \mathrm{e}^{-x} \mathrm{~d} x Γ ( α ) = ∫ 0 ∞ x α − 1 e − x d x 这是一个广义积分,当您第一次看到伽玛函数时,你有没有想过为什么要创造这样一个看起来很复杂又无规律的积分函数?其实伽玛函数并不是凭空产生的。
伽玛函数的理由来自函数图像的绘图。在初中我们学过“描点”绘图,比如要绘出y = x 2 y=x^2 y = x 2 x x x x x x n n n n = − 2 , − 1 , 0 , 1 , 2 n=-2,-1,0,1,2 n = − 2 , − 1 , 0 , 1 , 2 y = n 2 y=n^2 y = n 2 y = x 2 y=x^2 y = x 2 y = n 2 y=n^2 y = n 2
有了这个想法,我们现在要问一个问题:y = x ! y=x! y = x ! x x x 阶乘 定义 )
我们已经知道5 ! = 5 ∗ 4 ∗ 3 ∗ 2 ∗ 1 , 4 ! = 4 ∗ 3 ∗ 2 ∗ 1 , . . .1 ! = 1 5!=5*4*3*2*1, 4!=4*3*2*1,... 1!=1 5 ! = 5 ∗ 4 ∗ 3 ∗ 2 ∗ 1 , 4 ! = 4 ∗ 3 ∗ 2 ∗ 1 , ...1 ! = 1 n ! n! n ! y = x ! y=x! y = x !
我们把问题在具体一点,那 y = 1 2 ! y=\frac{1}{2} ! y = 2 1 ! y = 1 2 ! y=\frac{1}{2} ! y = 2 1 ! Γ ( s + 1 ) = s Γ ( s ) ( s > 0 ) \Gamma(s+1)=s \Gamma(s)(s>0) Γ ( s + 1 ) = s Γ ( s ) ( s > 0 ) Γ ( 1 2 ) = π \Gamma\left(\frac{1}{2}\right)=\sqrt{\pi} Γ ( 2 1 ) = π y = n ! y=n ! y = n ! 高等数学伽玛函数教程
核心结论来了:伽玛函数可以理解为阶乘函数。他把阶乘的定义域从正整数扩展到了实数
进一步的,一说到阶乘,你想到了什么?当然是排列组合了,在一开始的排列组合 会遇到大量阶乘运算,但是传统的阶乘都是正整数运算,伽玛函数相当于把定义域从正整数扩展到了整个实数范围内。
现在我们捋一捋其中的逻辑关系:
排列组合 ⇔ \Leftrightarrow ⇔ ⇔ \Leftrightarrow ⇔
所以,阶乘运算相当于桥梁,联系起了 “排列组合”和“伽玛函数”的内在关系。 也因此,你会在概率论的密度函数里,会有大量的伽玛函数出现。 理解了伽玛函数后,就可以引入伽玛分布了。
为什么要引入伽玛分布 在理解Gamma分布前,让我们思考以下几个问题:
1.为什么我们要发明Gamma分布?(也就是说,为什么这个分布会存在?)
2.什么时候应该用Gamma分布来做模型?我们为什么要发明Gamma分布?
答案:为了预测未来事件发生前的等待时间。 嗯?难道这不是指数分布的研究的问题? 那么,指数分布和Gamma分布的区别是什么呢?
指数分布描述的是独立事件的等待时间。而Gamma分布描述的是直到 k 个事件发生时的等待时间
简单的来说,指数分布解决的问题是“要等到一个随机事件发生,需要经历多久时间”,伽玛分布解决的问题是“要等到 k 个随机事件都发生,需要经历多久时间”
指数分布(Exponential Distribution)对应几何分布
伽马分布(Gamma Distribution)对应负二项分布
推导伽玛分布的密度函数PDF 在指数分布中,我们从泊松过程推导出了指数分布的PDF(详见此处 )。 要很好地理解Gamma分布,需要很好地理解它们。我们的学习顺序应该是:1.泊松分布,2.指数分布,3.gamma分布。
Gamma分布的PDF的推导与指数分布PDF的推导非常相似,除了一点--它是到第 k 个事件的等待时间,而不是第1个事件。
T T T k k k λ \lambda λ k k k λ \lambda λ P ( T > t ) P(T>t) P ( T > t ) k k k t t t P ( X = k ∣ P(X=k | P ( X = k ∣ t t t ) ) ) t t t k k k
上面预订了参数,现在看看怎么推导出伽玛分布的密度函数PDF。要得到密度函数需要先得到伽玛分布的分布函数CDF,然后对CDF微分就是密度函数。
分布函数C D F CDF C D F
P ( T ≤ t ) = 1 − P ( T > t ) = 1 − P ( 0 , 1 , 2 , … K − 1 事件发生在 [ 0 , t ] ) = 1 − ∑ x = 0 k − 1 ( λ t ) x e − λ t x ! \begin{aligned}
P(T \leq t) & =1-P(T>t) \\
& =1-P(0,1,2, \ldots K-1 \text { 事件发生在 }[0, t]) \\
& =1-\sum_{x=0}^{k-1} \frac{(\lambda t)^x e^{-\lambda t}}{x!}
\end{aligned} P ( T ≤ t ) = 1 − P ( T > t ) = 1 − P ( 0 , 1 , 2 , … K − 1 事件发生在 [ 0 , t ]) = 1 − x = 0 ∑ k − 1 x ! ( λ t ) x e − λ t 第一步:与指数分布的推导完全相同,除了多个事件,而不是在 T T T
第三步:x x x
对分布函数C D F CDF C D F P D F PDF P D F
d d t ( C D F ) = d d t ( 1 − ∑ x = 0 k − 1 ( λ t ) x e − λ t x ! ) \frac{d}{d t}(C D F)=\frac{d}{d t}\left(1-\sum_{x=0}^{k-1} \frac{(\lambda t)^x e^{-\lambda t}}{x!}\right) d t d ( C D F ) = d t d ( 1 − x = 0 ∑ k − 1 x ! ( λ t ) x e − λ t ) 现在,让我们对它进行微分。
为了便于微分,我们把 x = 0 x=0 x = 0 ( e − λ t ) \left(e^{-\lambda t}\right) ( e − λ t )
我们得到了Gamma分布的PDF。
这个推导看起来很复杂,但我们只是重新排列变量,应用微分的乘积法则,再到求和,并划掉一些常数项,毕竟常数项的微分等于 0 。
如果你看一下推导的最终输出,当 k = 1 k=1 k = 1 k k k k k k Γ ( k ) = ( k − 1 ) \Gamma(k)=(k-1) Γ ( k ) = ( k − 1 ) Γ \Gamma Γ
λ e − λ t ( λ t ) k − 1 ( k − 1 ) ! = λ e − λ t λ k − 1 t k − 1 ( k − 1 ) ! = λ k t k − 1 e − λ t ( k − 1 ) ! = λ k t k − 1 e − λ t Γ ( k ) \begin{aligned}
\frac{\lambda e^{-\lambda t}(\lambda t)^{k-1}}{(k-1)!} & =\frac{\lambda e^{-\lambda t} \lambda^{k-1} t^{k-1}}{(k-1)!} \\
& =\frac{\lambda^k t^{k-1} e^{-\lambda t}}{(k-1)!} \\
& =\frac{\lambda^k t^{k-1} e^{-\lambda t}}{\Gamma(k)}
\end{aligned} ( k − 1 )! λ e − λ t ( λ t ) k − 1 = ( k − 1 )! λ e − λ t λ k − 1 t k − 1 = ( k − 1 )! λ k t k − 1 e − λ t = Γ ( k ) λ k t k − 1 e − λ t 如果事件的到达遵循速率为 λ \lambda λ k k k Γ ( k , λ ) \Gamma(k, \lambda) Γ ( k , λ )
Gamma分布参数:一个shape一个scale?
第一:它有两种的参数集:
-( α , β ) (\alpha, \beta) ( α , β ) ( k , θ ) (k, \theta) ( k , θ ) ( α , β ) (\alpha, \beta) ( α , β ) k k k λ \lambda λ k k k α , λ \alpha, \lambda α , λ β \beta β ( k , θ ) (k, \theta) ( k , θ ) k k k θ \theta θ λ \lambda λ [ [ [ ] ] ]] ]]
仅仅是PDF表达形式不同而已,所以两种参数化都会产生统一的模型。就像用参数来描述直线,有些人使用 x x x y y y λ \lambda λ λ \lambda λ λ \lambda λ ( α , β ) (\alpha, \beta) ( α , β )
第二,有些学者称 λ \lambda λ θ = 1 / λ \theta=1 / \lambda θ = 1/ λ k k k λ \lambda λ ( k (k ( k λ \lambda λ k k k λ \lambda λ
眼见为实! 让我们来想象一下
K : 你等待发生的事件的数量。 λ \lambda λ
对于一个固定的比率 λ \lambda λ k k k T T T
对于固定数量的事件 k k k λ \lambda λ T T T
例假设某电话总机收到的电话数服从泊松过程,其中每分钟平均有5个.求第个电话后不到一分钟就有第二个电话的概率是多少?
解 泊松过程中两个泊松事件发生的时间间隔服从伽玛分布 β = 0.2 , α = 2. X \beta=0.2, \alpha=2 . X β = 0.2 , α = 2. X
P ( X ⩽ 1 ) = ∫ 0 1 1 β 2 x e − x / β d x = 25 ∫ 0 1 x e − 5 x d x = 1 − e − 5 ( 1 + 5 ) = 0.96. P(X \leqslant 1)=\int_0^1 \frac{1}{\beta^2} x e^{-x / \beta} d x=25 \int_0^1 x e^{-5 x} d x=1-e^{-5}(1+5)=0.96 . P ( X ⩽ 1 ) = ∫ 0 1 β 2 1 x e − x / β d x = 25 ∫ 0 1 x e − 5 x d x = 1 − e − 5 ( 1 + 5 ) = 0.96. 再次分析在本例题里参数意义,因为要求的是“第二个电话概率”,所以事件数量n = 2 n=2 n = 2 α \alpha α α = 2 \alpha=2 α = 2 λ = 5 \lambda=5 λ = 5 λ \lambda λ β \beta β β = 1 / λ = 1 / 5 = 0.2 \beta=1/\lambda=1/5=0.2 β = 1/ λ = 1/5 = 0.2 指数分布 的介绍,他通常叫做速率
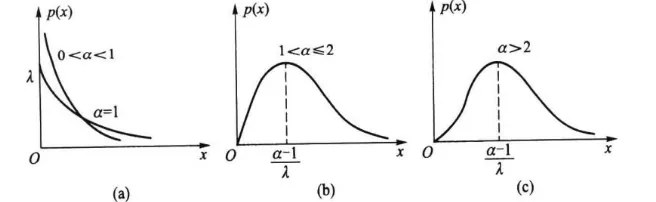
参数图
图2.5.6 给出若干条 λ \lambda λ α \alpha α
当 0 < α < 1 0<\alpha<1 0 < α < 1 p ( x ) p(x) p ( x ) x = 0 x=0 x = 0
当 α = 1 \alpha=1 α = 1 p ( x ) p(x) p ( x ) x = 0 x=0 x = 0 p ( 0 ) = λ p(0)=\lambda p ( 0 ) = λ
当 1 < α ⩽ 2 1<\alpha \leqslant 2 1 < α ⩽ 2 p ( x ) p(x) p ( x )
当 2 < α 2<\alpha 2 < α p ( x ) p(x) p ( x ) α \alpha α p ( x ) p(x) p ( x ) α \alpha α
伽玛分布的应用 假设 x 1 , x 2 , … x n x_1, x_2, \ldots x_n x 1 , x 2 , … x n n n n n n n Y ( Y = X 1 + X 2 + … + X n ) Y\left(Y=X_1+X_2+\ldots+X_n\right) Y ( Y = X 1 + X 2 + … + X n ) Y ∼ Gamma ( α , β ) Y \sim \operatorname{Gamma}(\alpha, \beta) Y ∼ Gamma ( α , β ) Y ∼ Gamma ( α , λ ) Y \sim \operatorname{Gamma}(\alpha, \lambda) Y ∼ Gamma ( α , λ ) α = n \alpha=n α = n β \beta β λ \lambda λ λ \lambda λ
指数分布为 α = 1 \alpha=1 α = 1
伽玛分布的重要性在于它定义了一族分布,而某些分布族是它的特例,但伽玛分布本身在等待时间和可靠性问题方面也有重要的应用.指数分布描述了某个泊松事件发生的等待时间(或泊松事件的时间间隔),而给定数目泊松事件发生的等待时间(或空间)可由伽玛分布描述这个给定的泊松事件数即为伽玛密度函数中的参数a,因此很容易看出,a=1时即为指数分布,伽玛密度函数可以类似上面指数密度的方法得到,细节留给大家证明.下面是伽玛分布在等待时间上应用的一些例子.
虽然伽玛分布的起源是用来处理 α \alpha α
例生物医学试验中经常对老鼠做试验, 剂量反映调查用于确定毒物剂量对老鼠寿命的影响. 所研究的有毒物质为排人空气中的喷气燃料. 该试验确定在一定剂量的有毒物质下,老鼠的生存时间(按周计)具有伽玛分布 α = 5 , β = 10 \alpha=5, \beta=10 α = 5 , β = 10
解 令随机变量 X X X
P ( X ⩽ 60 ) = 1 β 5 ∫ 0 60 x σ − 1 e − x / β Γ ( 5 ) d x . P(X \leqslant 60)=\frac{1}{\beta^5} \int_0^{60} \frac{x^{\sigma-1} e^{-x / \beta}}{\Gamma(5)} d x . P ( X ⩽ 60 ) = β 5 1 ∫ 0 60 Γ ( 5 ) x σ − 1 e − x / β d x . 上述积分的求解可通过利用不完全伽玛函数, 该函数可以得到伽玛分布的累积分布. 不完全伽玛函数为:
F ( x ; α ) = ∫ 0 x y α − 1 e − y Γ ( α ) d y . F(x ; \alpha)=\int_0^x \frac{y^{\alpha-1} e^{-y}}{\Gamma(\alpha)} d y . F ( x ; α ) = ∫ 0 x Γ ( α ) y α − 1 e − y d y . 若令 y = x / β y=x / \beta y = x / β x = β y x=\beta y x = β y
P ( X ⩽ 60 ) = ∫ 0 6 y 4 e − y Γ ( 5 ) d y , P(X \leqslant 60)=\int_0^6 \frac{y^4 e^{-y}}{\Gamma(5)} d y, P ( X ⩽ 60 ) = ∫ 0 6 Γ ( 5 ) y 4 e − y d y , 在附表 A. 24 的不完全伽玛函数表中,上式可以记作 F ( 6 ; 5 ) F(6 ; 5) F ( 6 ; 5 )
P ( X ⩽ 60 ) = F ( 6 ; 5 ) = 0.715 P(X \leqslant 60)=F(6 ; 5)=0.715 P ( X ⩽ 60 ) = F ( 6 ; 5 ) = 0.715 例 由以前的数据知, 在某几个月内顾客对某产品的投诉服从参数 α = 2 , β = 4 \alpha=2, \beta=4 α = 2 , β = 4
解 令 X X X α = 2 , β = 4 \alpha=2 , \beta=4 α = 2 , β = 4 α \alpha α β \beta β X ⩾ 20 X \geqslant 20 X ⩾ 20
P ( X ⩾ 20 ) = 1 − 1 β α ∫ 0 20 x α − 1 e − x / β Γ ( α ) d x . P(X \geqslant 20)=1-\frac{1}{\beta^\alpha} \int_0^{20} \frac{x^{\alpha-1} e^{-x / \beta}}{\Gamma(\alpha)} d x . P ( X ⩾ 20 ) = 1 − β α 1 ∫ 0 20 Γ ( α ) x α − 1 e − x / β d x . 再令 y = x / β y=x / \beta y = x / β
P ( X ⩾ 20 ) = 1 − ∫ 0 5 y e − y Γ ( 2 ) d y = 1 − F ( 5 ; 2 ) = 1 − 0.96 = 0.04 , P(X \geqslant 20)=1-\int_0^5 \frac{y e^{-y}}{\Gamma(2)} d y=1-F(5 ; 2)=1-0.96=0.04, P ( X ⩾ 20 ) = 1 − ∫ 0 5 Γ ( 2 ) y e − y d y = 1 − F ( 5 ; 2 ) = 1 − 0.96 = 0.04 , 查表 得 F ( 5 ; 2 ) = 0.96 F(5 ; 2)=0.96 F ( 5 ; 2 ) = 0.96 α = 2 , β = 4 \alpha=2, \beta=4 α = 2 , β = 4
伽马分布 G a ( α , λ ) G a(\alpha, \lambda) G a ( α , λ ) 利用伽马函数的性质, 不难算得伽马分布 G a ( α , λ ) G a(\alpha, \lambda) G a ( α , λ )
E ( X ) = λ α Γ ( α ) ∫ 0 ∞ x α e − λ x d x = Γ ( α + 1 ) Γ ( α ) 1 λ = α λ , E(X)=\frac{\lambda^\alpha}{\Gamma(\alpha)} \int_0^{\infty} x^\alpha \mathrm{e}^{-\lambda x} \mathrm{~d} x=\frac{\Gamma(\alpha+1)}{\Gamma(\alpha)} \frac{1}{\lambda}=\frac{\alpha}{\lambda}, E ( X ) = Γ ( α ) λ α ∫ 0 ∞ x α e − λ x d x = Γ ( α ) Γ ( α + 1 ) λ 1 = λ α , 又因为
E ( X 2 ) = λ α Γ ( α ) ∫ 0 ∞ x α + 1 e − λ x d x = Γ ( α + 2 ) λ 2 Γ ( α ) = α ( α + 1 ) λ 2 , E\left(X^2\right)=\frac{\lambda^\alpha}{\Gamma(\alpha)} \int_0^{\infty} x^{\alpha+1} \mathrm{e}^{-\lambda x} \mathrm{~d} x=\frac{\Gamma(\alpha+2)}{\lambda^2 \Gamma(\alpha)}=\frac{\alpha(\alpha+1)}{\lambda^2}, E ( X 2 ) = Γ ( α ) λ α ∫ 0 ∞ x α + 1 e − λ x d x = λ 2 Γ ( α ) Γ ( α + 2 ) = λ 2 α ( α + 1 ) , 由此得 X X X
Var ( X ) = E ( X 2 ) − [ E ( X ) ] 2 = α ( α + 1 ) λ 2 − ( α λ ) 2 = α λ 2 . \operatorname{Var}(X)=E\left(X^2\right)-[E(X)]^2=\frac{\alpha(\alpha+1)}{\lambda^2}-\left(\frac{\alpha}{\lambda}\right)^2=\frac{\alpha}{\lambda^2} . Var ( X ) = E ( X 2 ) − [ E ( X ) ] 2 = λ 2 α ( α + 1 ) − ( λ α ) 2 = λ 2 α . 伽马分布的两个特列 (1) α = 1 \alpha=1 α = 1
G a ( 1 , λ ) = Exp ( λ ) . G a(1, \lambda)=\operatorname{Exp}(\lambda) . G a ( 1 , λ ) = Exp ( λ ) . (2) 称 α = n / 2 , λ = 1 / 2 \alpha=n / 2, \lambda=1 / 2 α = n /2 , λ = 1/2 n n n χ 2 \chi^2 χ 2 χ 2 ( n ) \chi^2(n) χ 2 ( n )
G a ( n 2 , 1 2 ) = χ 2 ( n ) , G a\left(\frac{n}{2}, \frac{1}{2}\right)=\chi^2(n), G a ( 2 n , 2 1 ) = χ 2 ( n ) , 其密度函数为
p ( x ) = { 1 2 n 2 Γ ( n 2 ) e − x 2 x n 2 − 1 , x ⩾ 0 , 0 , x < 0. p(x)= \begin{cases}\frac{1}{2^{\frac{n}{2}} \Gamma\left(\frac{n}{2}\right)} \mathrm{e}^{-\frac{x}{2} x^{\frac{n}{2}-1}}, & x \geqslant 0, \\ 0, & x<0 .\end{cases} p ( x ) = ⎩ ⎨ ⎧ 2 2 n Γ ( 2 n ) 1 e − 2 x x 2 n − 1 , 0 , x ⩾ 0 , x < 0. 这里 n n n χ 2 \chi^2 χ 2 χ 2 \chi^2 χ 2
因为 χ 2 \chi^2 χ 2 χ 2 \chi^2 χ 2
E ( X ) = n , Var ( X ) = 2 n . E(X)=n, \quad \operatorname{Var}(X)=2 n .
E ( X ) = n , Var ( X ) = 2 n . 例电子产品的失效常常是由于外界的"冲击引起". 若在 ( 0 , t ) (0, t) ( 0 , t ) N ( t ) N(t) N ( t ) λ t \lambda t λ t n n n S n S_n S n G a ( n , λ ) G a(n, \lambda) G a ( n , λ )
证明 因为事件"第 n n n S n S_n S n t t t ( 0 , t ) (0, t) ( 0 , t ) N ( t ) N(t) N ( t ) n n n
{ S n ⩽ t } = { N ( t ) ⩾ n } . \left\{S_n \leqslant t\right\}=\{N(t) \geqslant n\} . { S n ⩽ t } = { N ( t ) ⩾ n } . 于是, S n S_n S n
F ( t ) = P ( S n ⩽ t ) = P ( N ( t ) ⩾ n ) = ∑ k = n ∞ ( λ t ) k k ! e − λ t F(t)=P\left(S_n \leqslant t\right)=P(N(t) \geqslant n)=\sum_{k=n}^{\infty} \frac{(\lambda t)^k}{k!} \mathrm{e}^{-\lambda t} F ( t ) = P ( S n ⩽ t ) = P ( N ( t ) ⩾ n ) = k = n ∑ ∞ k ! ( λ t ) k e − λ t 用分部积分法可以验证下列等式
∑ k = 0 n − 1 ( λ t ) k k ! e − λ t = λ n Γ ( n ) ∫ t ∞ x n − 1 e − λ x d x \sum_{k=0}^{n-1} \frac{(\lambda t)^k}{k!} \mathrm{e}^{-\lambda t}=\frac{\lambda^n}{\Gamma(n)} \int_t^{\infty} x^{n-1} \mathrm{e}^{-\lambda x} \mathrm{~d} x k = 0 ∑ n − 1 k ! ( λ t ) k e − λ t = Γ ( n ) λ n ∫ t ∞ x n − 1 e − λ x d x 所以
F ( t ) = λ n Γ ( n ) ∫ 0 t x n − 1 e − λ x d x 这就表明 S n ∼ G a ( n , λ ) . 证毕。 \begin{aligned}
&F(t)=\frac{\lambda^n}{\Gamma(n)} \int_0^t x^{n-1} \mathrm{e}^{-\lambda x} \mathrm{~d} x\\
&\text { 这就表明 } S_n \sim G a(n, \lambda) \text {. 证毕。 }
\end{aligned} F ( t ) = Γ ( n ) λ n ∫ 0 t x n − 1 e − λ x d x 这就表明 S n ∼ G a ( n , λ ) . 证毕。 关于更多概率分布表见附录1:常见概率分布表
实例 我们可以在使用指数分布的所有应用中使用gamma分布,例如:
等待时间建模
可靠性(故障)建模
服务时间建模(排队理论)因为指数分布是伽玛分布的特例(只需将 1 代入 k k k
排队理论实例
你去了KFC,并加入队伍开始排队,前面有两个人。排在第一个的正在下单中,排在第二的人正在等待。他们的服务时间 S 1 S 1 S 1 S 2 S 2 S 2
问题:你在队列中等待超过 5 分钟的概率是多少?
P ( T > 5 ) = P ( 在 [ 0 , 5 ] 中发生的次数少于 2 ) = ∑ x = 0 1 ( λ t ) x e − λ t x ! = 0.2873 \begin{aligned}
P(T>5) & =P(\text { 在 }[0,5] \text { 中发生的次数少于 } 2) \\
& =\sum_{x=0}^1 \frac{(\lambda t)^x e^{-\lambda t}}{x!} \\
& =0.2873
\end{aligned} P ( T > 5 ) = P ( 在 [ 0 , 5 ] 中发生的次数少于 2 ) = x = 0 ∑ 1 x ! ( λ t ) x e − λ t = 0.2873 我们所做的就是把 t = 5 t=5 t = 5 λ = 0.5 \lambda=0.5 λ = 0.5
我在 KFC 餐厅等待超过 5 分钟的机会不到 30 % 30 \% 30% k k k
3.伽马分布的特殊情况
埃朗分布Erlang和伽玛Gamma的区别在于,在Gamma分布中,k k k k k k
{width=600px}
 {width=300px}
然后我们就想当然的认为和长相类似,后者就是前者的粗略版。
{width=300px}
然后我们就想当然的认为和长相类似,后者就是前者的粗略版。