17._连续性_一般正态分布化为标准正态分布-Part3 - 概率论与数理统计

为什么要把一般正态分布化为标准正态分布？

因为正态分布表只提供标准正态分布的数据查询，因此需要把一般正态分布转化为标准正态分布。

坐标平移转换公式

在进行下面讲解前，先介绍一个预备知识：图像平移，如下图，假设有一个二次函数，他的图像如下图(红色曲线) $y=4(x-4)^2 ...①$ ，而我们知道②式平方口诀表 $y'=x'^2 ...②$ 如何把①变换为②的模式？答案就是使用简单的线性变换：如果我们把①稍微变形为 $y=[2(x-4)]^2 ...③$ 然后令 $x'=(x-4), y'=y$ 带入③ 就可以直接得到②式 $y'=(2x')^2$ 这样就可以继续使用平方口诀表了。注意：此时值的变换，在①原式里，原来是求当 $x=6$ 时， $y=16$ 而在新变换③里，需要计算 $x'=2(x-4)=4$ 的值, 此时 $y'=16$ 图像平移示意图参考下图。 {width=500px}

一般正态分布化为标准正态分布

一般正态分布的概率密度和分布函数为：

\begin{aligned} & \varphi(x)=\dfrac{1}{\sqrt{2 \pi} \sigma} e^{-\dfrac{(x-\mu)^2}{2 \sigma^2}} \\ & \Phi(x)=\dfrac{1}{\sqrt{2 \pi} \sigma} \int_{-\infty}^x e^{-\dfrac{(t-\mu)^2}{2 \sigma^2}} d t . \end{aligned} ...(1)

当 $\mu=0,\sigma=1$ 时称为标准正态分布，所以标准正态分布的的概率密度和分布函数为：

\begin{aligned} & \varphi_0(x)=\frac{1}{\sqrt{2 \pi}} \cdot \mathrm{e}^{-\frac{x^2}{2}} \\ & \Phi_0(x)=\frac{1}{\sqrt{2 \pi}} \int_{-\infty}^x e^{-\frac{t^2}{2}} d t, \\ \end{aligned} ...(2)

现在要把(1)式化为(2)式，一般正态分布(1)的密度函数，可以写成

\varphi(x)= \dfrac{1}{\sigma} \left [ \dfrac{1}{\sqrt{2\pi} } e^{-\dfrac{(\frac{x-\mu}{\sigma})^2}{2 }}\right] ...(3)

把 $\frac{x-\mu}{\sigma}$ 看成一个整体，则(3)式方括号里面就是标准正态分布，即

\varphi(x) = \dfrac{1}{\sigma}\varphi_0 \left(\frac{x-\mu}{\sigma} \right) \\ \varphi(x) = \dfrac{1}{\sigma}\varphi_0 \left(\frac{x-\mu}{\sigma} \right) \\ ...(4)

在参考上面引例的说明，由此就可以得到一般正态分布化为标准化的方法

一般正态分布化为标准正态分布

设随机变量 $X \sim N\left(\mu, \sigma^2\right)$ ，如果做可逆的变量代换 $X^{\prime}=\frac{X-\mu}{\sigma}$ ，那么

f\left(x^{\prime}\right)=\frac{1}{\sqrt{2 \pi}} e^{-\frac{x^{\prime 2}}{2}}

即 $X^{\prime} \sim N(0,1)$ ，是标准正态分布。我们把上述变量替换称作正态分布的标准化，并得到一般正态分布转化为标准正态分布的转化公式，即

\boxed{ \begin{aligned} &\varphi(x) = \dfrac{1}{\sigma}\varphi_0 \left(\frac{x- \mu}{\sigma} \right) \\ &\Phi(x)= \Phi_0(x) \left(\frac{x- \mu}{\sigma} \right) \end{aligned} ...(*) }

这样，研究任意正态分布仅需研究标准正态分布的情形即可。

提示：如果上面推导你实在不理解也没关心，只要记住转换公式就可以了。

标准化的通俗解释

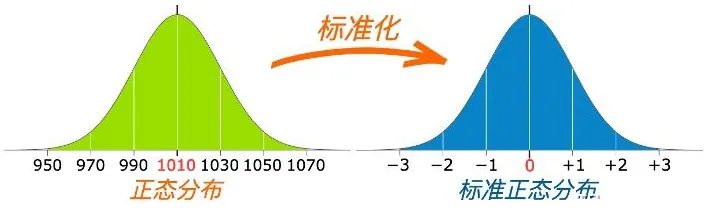
把一般正态分布转化为标准正态分布，原来的曲线的形状不会变化，即不会改变图像的高矮胖瘦，只是位置发生平移，比如下图中的例子，经过标准化实际上只是均数从1010移到了0。 $图片$ {width=500px}

标准正态分布性质

标准正态分布 $x \sim N(0,1)$ 有如下性质:

概率密度函数图像是关于 $x=0$ 对称的，根据函数的奇偶性，所以 $f(-x)=f(x)$ ;
概率密度函数图像在 $x=0$ 处达到极大（也是最大）；
分布函数有性质 $F(-x)=1-F(x)$ . 关于最后一点的性质，可以参考附录1：置信区间与上 $\alpha$ 分位数

若 $X \sim N\left(\mu, \sigma^2\right)$ ，则可利用标准正态分布函数 $\Phi(x)$ 通过查附录求得 $X$ 落在任一区间 $(a, b](a<b)$ 内的概率，即

\begin{aligned} P(a<X \leqslant b) & =P\left(\frac{a-\mu}{\sigma}<\frac{X-\mu}{\sigma} \leqslant \frac{b-\mu}{\sigma}\right) \\ & =P\left(\frac{X-\mu}{\sigma} \leqslant \frac{b-\mu}{\sigma}\right)-P\left(\frac{X-\mu}{\sigma} \leqslant \frac{a-\mu}{\sigma}\right) \\ & =\Phi\left(\frac{b-\mu}{\sigma}\right)-\Phi\left(\frac{a-\mu}{\sigma}\right) \end{aligned}

例 设随机变量 $X \sim N(0,1)$ ，查表求下列概率值: (1) $P(-1<X \leq 1.22)$ ; (2) $P(|X| \leq 1.22)$ 解 (1) 查表并计算可得

\begin{aligned} P(-1<X \leq 1.22) & =\Phi(1.22)-\Phi(-1)=\Phi(1.22)-(1-\Phi(1)) \\ & =0.8888-1+0.8413=0.7301 \end{aligned}

(2) 同样地

\begin{aligned} P(|X| \leq 1.22) & =P(-1.22 \leq X \leq 1.22)=\Phi(1.22)+\Phi(-1.22) \\ & =2 \Phi(1.22)-1=0.7776 \end{aligned}

例设 $X \sim N(1,4)$ ，求 $F(5) 、 P(0<X \leqslant 1.6) 、 P(|X-1| \leqslant 2)$ ．解这里 $\mu=1, \sigma=2$ ，故

\begin{gathered} F(5)=P(X \leqslant 5)=P\left(\frac{X-1}{2} \leqslant \frac{5-1}{2}\right)=\Phi\left(\frac{5-1}{2}\right)=\Phi(2) \approx 0.9772 \\ P(0<X \leqslant 1.6)=\Phi\left(\frac{1.6-1}{2}\right)-\Phi\left(\frac{0-1}{2}\right)=\Phi(0.3)-\Phi(-0.5) \\ =0.6197-[1-\Phi(0.5)]=0.6197-(1-0.6915)=0.3094 \\ \begin{aligned} P(|X-1| \leqslant 2) & =P(-1 \leqslant X \leqslant 3)=P\left(-1 \leqslant \frac{X-1}{2} \leqslant 1\right)=\Phi(1)-\Phi(-1)=2 \Phi(1)-1 \\ & =2 \times 0.8413-1=0.6826 \end{aligned} \end{gathered}