正态分布表的使用
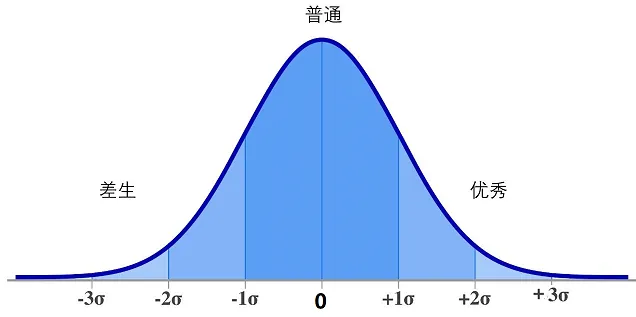
在介绍标准正态分布 x∼N(0,1)时提到,标准正态分布密度函数图像 如下
 {width=550px}
{width=550px}
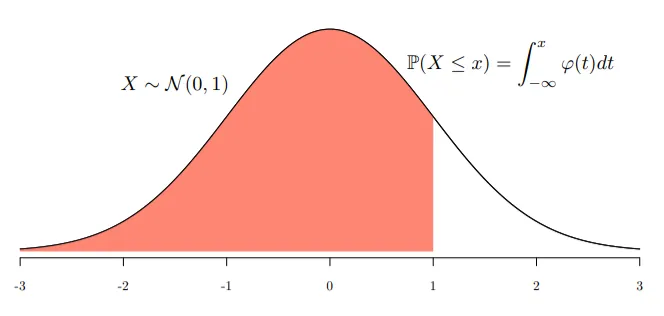
标准正态分布的密度函数图像的意义
 {width=550px}
{width=550px}
从上面两个图里可以知道正态分布有如下性质:
性质1. 概率密度函数图像是关于 x=0 对称的,根据函数的奇偶性,所以 φ0(−x)=φ0(x);
性质2 概率密度函数图像在 x=0 处达到极大(参考密度函数图像,很容易理解);
性质3 分布函数有性质 Φ0(−x)=1−Φ0(x),且Φ0(u)=0.5
请务必牢记分布函数的定义,分布函数F(X)=P(X⩽x)他是一个累加值。比如考试分F(90)=P(X<90)=80 表示分数小于90分的人数为80人,F(60)=P(X<60)=20 表示分数小于60分的人数为20人, 现在要求分数在60−90之间的人数,显然就是F(90)−F(60)=80−20=60人,分布函数求导就是密度函数,密度函数积分就是分布函数。而积分的本质就是求面积,所以密度函数曲线围成的整个面积就是所有的概率为1.通常认为分布函数的作用用来计算密度函数,单纯看分布函数图像其实看不出多少有价值的东西。数学上的表达就是密度函数在区间(a,b)上的积分。所以,概率的大小就是“概率密度函数曲线下的面积”的大小,这个不太起眼的概念实际上就决定了你日后是否能理解假设检验中所谓的“拒绝域”。
性质3可以通过正态密度函数的积分进行计算,但是我们准备从密度函数的图像上来解释一下Φ0(−x)=1−Φ0(x)的意义。
根据分布函数的定义,他表示的是概率的累加值,而所有概率的可能性为100%,所以分布函数的整体值就是1。也就是说,密度函数曲线下所围成的总面积为1.
例求Φ0(−2)
解:
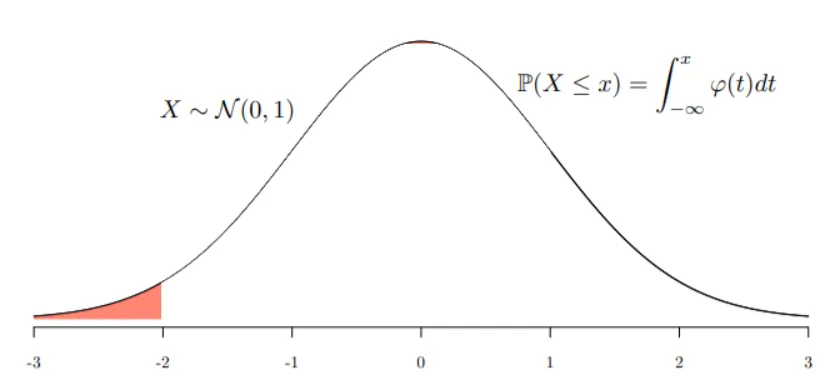
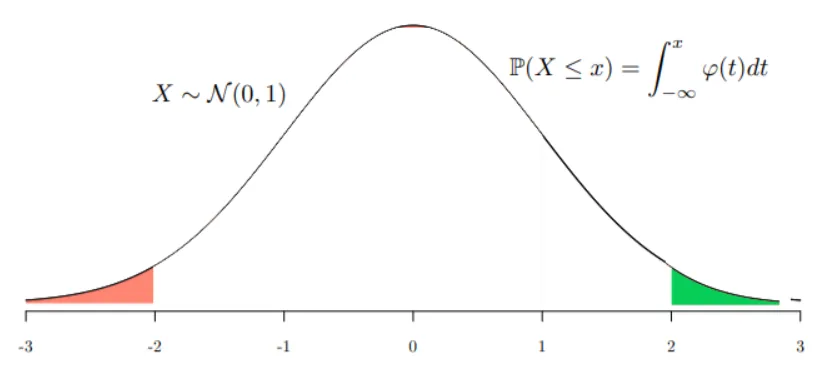
STEP1 要求Φ0(−2),根据分布函数的定义即是求Φ0(−2)=P(X≤−2) ,也就是求红色区域的面积。
 {width=400px}
{width=400px}
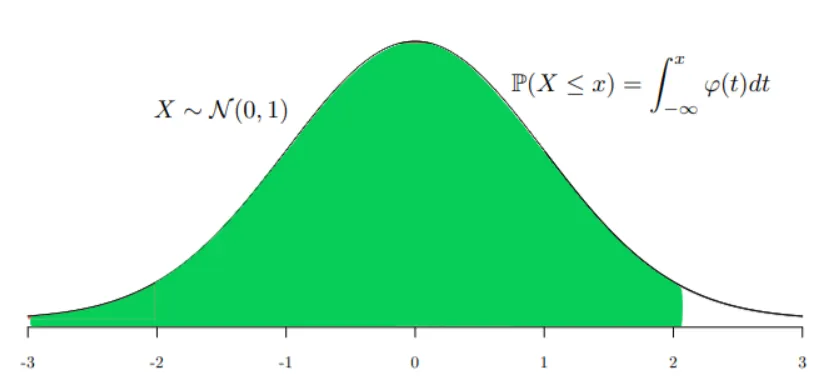
STEP2 很遗憾,从正态表里,查不到Φ0(−2),但是根据对称性可以查到 Φ0(2) ,而Φ0(2)=P(X≤2) 表示的下图绿色图形的面积。
 {width=400px}
{width=400px}
STEP3 我们用总面积减去上面大的绿色曲面面积,就可以得到下图小的绿色曲面面积。
 {width=400px}
{width=400px}
STEP4 根据对称性,上图红色曲面面积就等于小的绿色曲面面积。
STEP5 因此,查表知 Φ0(2)=0.9772,所以 Φ0(−2)=1−0.9772=0.0228
例求Φ0(1.65)
解:题目已经是标准正态分布,直接差表 Φ0(1.65)=0.9505
例 求标准正态分布,P{∣X∣≤2} 的值。
解:P{∣X∣≤2}=P{−2≤X≤2}
在例1里,已经算出其值,所以
=Φ0(2)−Φ0(−2)=0.972−0.0228=0.9492
下面我们再来分析一下例3的题目:
P{∣X∣≤2}=Φ0(2)−Φ0(−2)
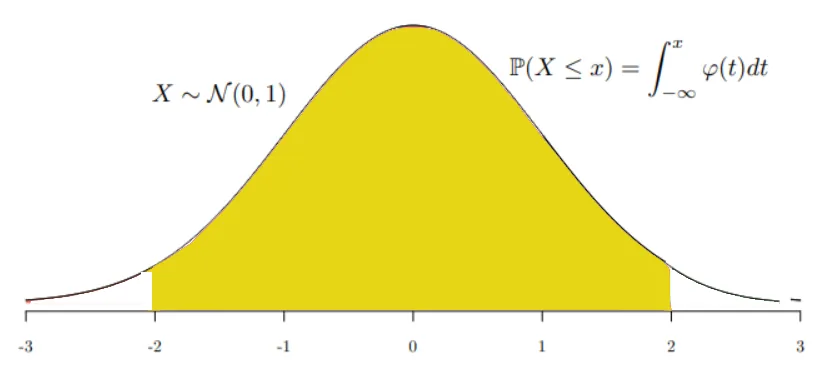
在例1里,已经知道Φ0(2) 表示的是大的绿色曲面面积
Φ0(−2) 表示的是左下角小的红色的曲面面积,因此这个结果是如下曲面面积
 {width=400px}
{width=400px}
例 有一批袋装大米,质量误差服从X∼N(50,1)的正态分布,求质量范围在49 51之间的概率。
解:这是一个一般正态分布,因X∼N(50,1),所以μ=50,σ=1
要求质量在49−51之间,就是求 P{49≤X≤51}=Φ(51)−Φ0(49)
利用上节介绍的一般正态分布化为标准正态分布公式:
Φ(x)=Φ0(x)(σx−μ) ,做一个线性变换的
Φ(51)−Φ(49)=Φ0(1)−Φ0(−1)=2Φ0(1)−1
标准正态分布的分位数概念
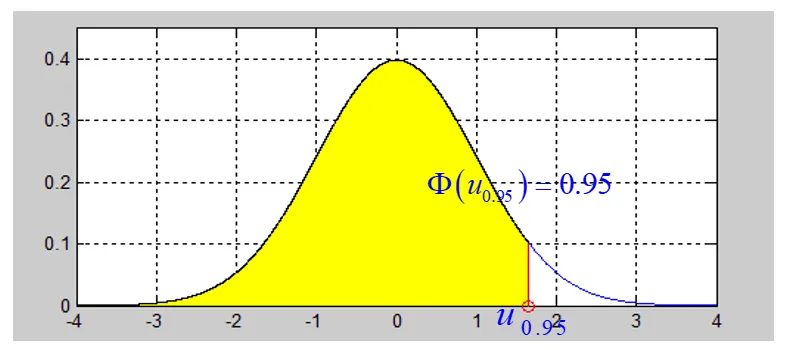
设 X∼N(0,1), 对给定的 α, 若 数 uα 满足
Φ(uα)=∫−∞uαφ(x)dx=P(X≤uα)=α 称 uα 为随机变量X的 α− 分位数
分位数的几何意义
 {width=500px}
{width=500px}
上 α 分位数 与下 α 分位数
为什么要引入分位数?其实就方便统计,比如班级里考试,这次考试有30%的同学考试成绩超过90分,在这句话里, 90分就是一个分为点,他把整个成绩分成了90分上和90分下,而 30% 则包含了90分以上的占比。
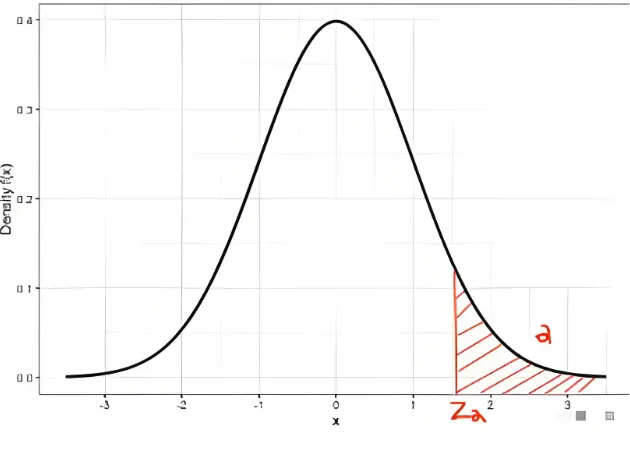
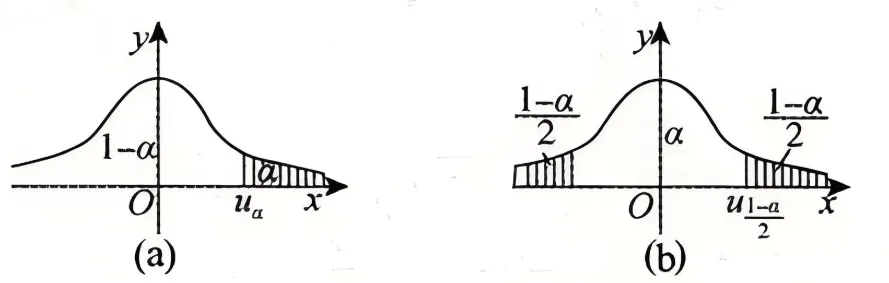
上 α 分位数 定义 P=(X⩾Za)=a, 在标准正态分布的概率分布图中, 临界值右侧曲线下的面积大小为 a (下图)。
 {width=300px}
{width=300px}
根据定义其意思等价于
∫zα+∞f(z)dz=α 或者 ∫−∞zαf(z)dz=1−α ,其中 f(z) 是 Z 的概率分布函数。
右侧尾部的阴影部分面积为α,这个区域在右单侧检验时也叫拒绝域或否定域。α也称(差异)显著性水平,置信水平则等于接受域的面积1−α 。
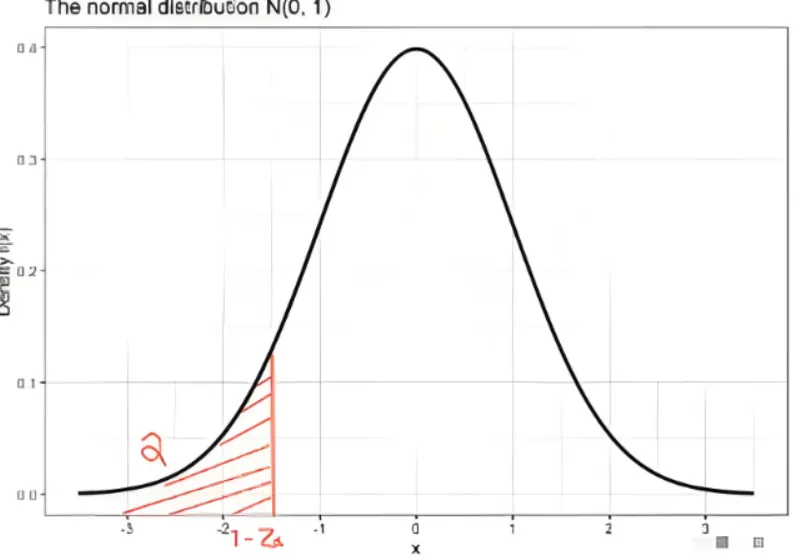
下a 分位数, 则是 P=(X⩽Z1−a)=a, 临界值左侧曲线下的面积大小为 a (下图)。
 {width=300px}
{width=300px}
根据定义:随机变量 Z 的下 α 分位点 z1−α 满足:P{Z<z1−α}=α, 0<α<1 .
即 ∫−∞z1−αf(z)dz=α 或者 ∫z1−α+∞f(z)dz=1−α ,其中 f(z) 是 Z 的概率分布函数。
注意:记号 z1−α 的定义来自 ∫z1−α+∞f(z)dz=1−α ,表示该点右侧累积概率为 1−α ,满足下 α 分位点的定义。
另一种记法(已经不能显示"下"的意思了)P{Z>z1−α}=1−α, 0<α<1 .
下a 分位点通常作为左单侧检验或者双侧尾部检验的参考值,与假设命题、置信水平或显著性水平配合使用。
概率统计背景
要理解上 α 分位数 与下 α 分位数 这其中的区别还是需要一点小常识。
总体来说,全国各大高校统计真题分为五大门派:纯贾、贾茆、纯茆、贾Pro、茆Pro。
这里的贾不仅仅指贾俊平的《统计学》,而是以贾俊平《统计学》为代表的偏文、偏经济的一类教材,比如袁卫的《统计学》等。
同样,这里的茆不仅仅只是茆诗松的《概率论与数理统计》,而是以茆诗松《概率论与数理统计》为代表的偏数理的一类教材,比如盛骤的《概率论与数理统计》等。
 {width=500px}
{width=500px}
经过不断的合并,最后形成两点派别,贾派对应的高校包括中央财经大学、天津财经大学、西安科技大学等,茆派对应的高校包括北京师范大学、深圳大学、广东财经大学等
在贾书中,使用的是上分位数,而在茆书中,使用的却是下 α 分位数,所以对于贾书中的 Zα, 我们在茆书中查表的时候, 应该查找 Z(1−α), 以 α=0.05 为例, 当贾书中求标准正态分布的上 0.05 分位数时,我们査找茆书的时候,应该査找Z0.95=1.645,而不是Z0.05=1.645 所以一定要区分清楚!
目前,在考研老师出题里,我们一般使用的上 a 分位数,但是也有老师使用下a 分位数
例 设随机变量 X 服从正态分布 N(0,1) ,对给定的 α(0<α<1) ,数 uα 满足 P{X>uα}=α ,若 P{∣X∣<x}=α ,则 x 等于( ).
(A)u2α
(B)u1−2α
(C)u21−α
(D)u1−α
解 应选(C).
如图所示,从几何直观看,条件中给出的 uα 即为上侧 α 分位数。类比可得 P{∣X∣<u21−α}=α ,故选择(C).
例某学校规定划分考生成绩的等级方法如下:考试成绩的实际考分在前10%的为 A 等,考分在前 10% 以后但在前 50% 的为 B 等,考分在前 50% 以后但在前 85% 的为 C等,考分在后 10% 的为D等.某次期末考试中,设考生的成绩X服从正态分 布 X∼N(μ,σ2) ,经计算可知 μ=73,σ2=144 ,求这次期末考试等级划 分的具体分数线。
解 由题意可知 X∼N(73,144) ,则
P(X≥a)=1−Φ(12a−73)=0.1⇒(12a−73)=u0.9=1.282⇒a=88.384≈88 又 P(X≥b)=1−Φ(12a−73)=0.5⇒(12b−73)=u0.5=0⇒b=73 又 P(X≤c)=Φ(12a−73)=0.5⇒(12c−73)=u0.1=−u0.9=−1.282⇒c≈58 综述所求,可知,在此次考试中,分数在88.384以上的,为等级A,分数在73至88.384之间的,为等级B,分数在57.616至73之间的,为等级C,分数在57.616以下的,为等级D。90)
例 上α 分位数 在上面列子中知道,Φ0(−2)=0.0228 表示小的红色曲面面积如下图,但是,利用图像的对称性,我们也知道Φ0(2)右侧的绿色的曲面面积也等于0.0228, 我们把这个0.0228称作上α 分位数,记做 α0.0228
换句话说,上α 分位数可以看成是右侧小绿色曲面面积。
 {width=400px}
{width=400px}
例知某门课程考生分数 X 服从正态分布 N(75,102), 若把考生分数在后 10% 的评为 C 级, 则 C 级的分数线为 \hx 分. (结果四舍五入, 已知 Φ(1.285)=0.9, 其中 Φ(x) 为正态分布函数)
解:有 0.9=1−P(10X−75≤10x−75)=1−Φ(10x−75)=Φ(−10x−75)
则 −10x−75=1.285, 有 x=62.15
本节内容节选自 附录1:置信区间与上α分位数
正态分布表的使用方法
正态分布表如下图,为了让列表不太长,我们把 "0.1" 的值垂直排列,然后把每个 0.1 后面的 "0.01" 值水平排列。形成一个方表,也就是
第一列:0,0.1,0.2,3.0 精确到小数点的第一位
第一行:0,0.01,0.02,0.03...0.09 精确到小数点的第二位
因此要查一个数,比如 Φ0(1.96) 需要把1.96分解为1.9加上0.06, 然后按行找到1.9,按列找到0.06,即可得到0.975
再比如
Φ0(0)=0.5000 第一行第一列
Φ0(0.01)=0.5040 第一行第二列
Φ0(0.10)=0.5398 第二行第一列
Φ0(0.11)=0.5438 第二行第一列

 {width=550px}
{width=550px} {width=550px}
{width=550px} {width=400px}
{width=400px} {width=400px}
{width=400px} {width=400px}
{width=400px} {width=400px}
{width=400px} {width=500px}
{width=500px} {width=300px}
{width=300px} {width=300px}
{width=300px} {width=500px}
{width=500px}
 {width=400px}
{width=400px}