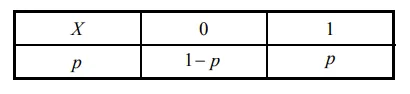本节简单的说,抽查一个产品,质量可能合格或者不合格,这是两点分布(也叫伯努利分布)。
理解常见的随机变量与分布
在学习本章内容时,会学习二项分布、泊松分别、指数分布、正态分布等,读者需要记住常见情况下使用哪种分布。比如医院急求病人分布,轮胎损坏分布等,必须知道在这种情况下应该大致使用哪种分布。如果不了解每个分布应用的场景,将难于做题。考试基本上就考那几种场景。
伯努利试验
设对一随机试验 E ,我们只关心某个事件 A 发生与否,此时试验的结果可以看成只有两种: A 发生或者 A 不发生。那么称这个试验为伯努利试验.
比如产品质量的合格与不合格,投币的正面与反面,成绩的及格与不及格,对候选人的支持与不支持,足球比赛的输与赢,明天的下雨与不下雨,战争的胜利与失败,电力的超载与非超载等等都可以看成伯努利试验(Bernoulli distribution)。
对于伯努利实验,我们需要把他“数字化”,就像投硬币,如果用1表示正面,那么用0就就可以表示反面。 再如检查产品是否合格,如果用1表示合格,那么用0就表示不合格,因此我们引入伯努利分布:
伯努利分布(两点分布)
两点分布,国外叫做伯努利分布(Bernoulli distribution),因为他是伯努利发现的,国内在高中通常叫做0-1分布,到了大学通常叫做两点分布。
伯努利分布:
若随机变量 X 只可能取 x1 与 x2 两个值, 它对应取值的概率分别是
P{X=x1}=1−p,P{X=x2}=p(0<p<1), 则称 X 服从参数为 p 的叫做伯努利分布或者两点分布,记做X∼b(1,p).
这里,我们可以把结果 1 看作成功,把结果 0 看作失败。
因为这里X 取值为 X=0 或X=1 时, 所以伯努利分布布也称为 (0−1)分布, 记为 X∼(0−1) 分布,。
伯努利分布可以用下表列出。
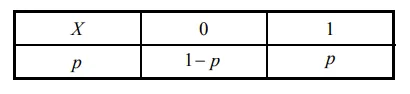
通俗理解,成功的概率为p, 失败的概率为1−p , 其分布列也可以写成函数形式,即
P(X=x)=px(1−p)1−x,x=0,1. 伯努利分布 b(1,p) 主要用来描述一次伯努利试验中成功的次数.一个服从伯努利分布的随机变量并没有太多用处但是,如果考虑多枚硬币或者不断地重复抛掷同1枚硬币,那么情况就会发生很大的变化这就是下一节介绍的二项分布。
伯努利分布应用场景
在一些随机试验中, 它的样本空间只包含两个元素,即 Ω={ω1,ω2}, 因此可以在 Ω 上定义一个服从 X∼(0−1) 分布的随机变量: X=X(ω)={0,1,ω=ω1ω=ω2 来描述随机试验结果. 因此,只包含两个基本事件的随机试验可以用两点分布来描述. 也就是说,若一个随机试验只关心某事件出现与否,则可用一个服从 (0−1) 分布的随机变量来描述。例如,抛一枚硬币试验中出现 "正面" 与 "反面" 的概率分布;产品抽验试验中 "正品"与 "次品"的概率分布等.
例 200 件产品中, 有 196 件是正品, 4 件是次品, 今从中随机地抽取一件, 若规定
X={1, 取到正品 0, 取到次品 则 P{X=1}=200196=0.98,P{X=0}=2004=0.02, 于是, X 服从参数为 0.98 的两点分布,即X∼b(1,0.98)
伯努利分布的数学期望和方差
从0-1分布表里不难得出
E(X)D(X)=1⋅p+0⋅q=p=E(X2)−[E(X)]2=12⋅p+02⋅(1−p)−p2=pq. 因此伯努利分布的数学期望和方差为
X∼b(1,p) 两点分布的数学期望: p
X∼b(1,p) 两点分布的方差: p(1−p)
例从装有 6 只白球和 8 只红球的口袋中任取一球,用 X 表示"取到的红球数",求 X的分布律.
解 X 的可能取值是 0,1 满足伯努利分布
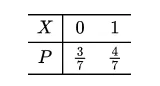
P{X=0}=C141C61=73,P{X=1}=C141C81=74 所以,X 的分布律如表 所示.
例一箱产品中只有 10 件,其中 8 件正品, 2 件次品.从中任取 1 件,设
X={1, 当取正品时, 0, 当取次品时 , 求 X 的分布律.
解 由已知,得 X∼(0−1) ,其中参数 p=P{X=1}=C101C81=54 .
所以,X 的分布律如表 所示.

从上面3个例子可以看到伯努利分布虽然简单,但是应用广泛。
初学者常见的疑问
问: 伯努利分布是一个离散型概率分布,所以只有概率质量函数 P(X) 而没有概率密度函数 f(x) ,并且 X 只定义在 {0,1} 而非 [0,1] 。那为什么要把 P(X) 写作 px∗(1−p)1−x ,而不是只给出其在 0 和 1 两个点的概率值 p 和 1−p 。为什么要为一个只在两点有定义的离散函数构造一个过这两点的定义更广的连续函数?
答: 伯努利分布是一个离散型概率分布,用于描述只有两个可能结果的随机试验,例如抛硬市的结果可以是正面(1)或反面(0)。在伯努利分布中,参数p表示事件的成功概率,而1-p表示事件的失败概率。
关于你提到的概率质量函数 P(X) ,通常会用px(1−p)1−x来表示。这里的 x 是伯努利随机变量X的取值,他是一个定值,就是只取0或1。让我们来解释一下为什么使用这个形式。
在伯努利分布中,我们需要考虑事件成功和失败的概率。当事件成功 (X=1) 时,我们希望概率质量函数给出 p 的概率值。当事件失败 (X=0) 时,我们希望概率质量函数给出 1−p 的概率值。
我们可以观察到,在 X=1 时, px(1−p)1−x=p 。同样地,在 X=0 时, px(1−p)1−x=(1−p) 。
这种写法的好处是,通过使用 px(1−p)1−x ,我们可以用一个统一的表达式来表示伯努利分布在 X=0 和 X=1 两个点上的概率。这样的表达形式更加紧凑和简洁。
虽然伯努利分布的定义域是离散的,只包括 0 和 1 ,但是通过引入连续函数的表示形式,我们可以更方便地与其他概率分布进行比较和推广。这种方式在概率论和统计学中是常见的做法,可以帮助我们更好地理解和分析不同的概率分布。
关于更多概率分布表见附录1:常见概率分布表