0.3 行列式

只用一个数概括一种多变量现象。这在数学中常常很有用，其中行列式就是一例。行列式只对方阵 $A \in M_{n}(\mathbf{F})$ 有定义，并且它可以按两种重要的，完全不同的等价方式来描述。我们把 $A \in M_{n}(\mathbf{F})$ 的行列式记作 $\det A$ 。

0.3.1 Laplace展开对 $A = \left[a_{ij}\right] \in M_n(\mathbf{F})$ 的行列式可归纳定义如下，假设行列式在 $M_{n}$ （F）上已定义，设 $A_{ij} \in M_{n - 1}(\mathbf{F})$ 表示从 $A \in M_{n}(\mathbf{F})$ 中划去第 $i$ 行和第 $j$ 列后得到的子矩阵．于是，对所有的 $i \leqslant n, j \leqslant n$

而这个相同的值就是det $A$ ，等式左边是依第 $\pmb{i}$ 行关于诸子式的Laplace展开式，而右边是依第 $\pmb{j}$ 列的Laplace展开式[见(0.7.1)]．对于任意选择的行和列，其中任一展开式都得到 $\pmb{A}$ 的行列式．归纳过程从 $1\times 1$ 矩阵开始，定义它的行列式为单个元的值．于是

等等，显然，如果 $A \in M_n(\mathbf{C})$ ，则 $\det A^r = \det A$ ， $\prod_{i} \det A^i = \overline{\det A}$ 。

0.3.2 交错和 受上述低维例子的启发，对于 $A = [a_{ij}] \in M_n(\mathbb{F})$ ，还有

其中，求和取遍1，2，…，n的所有n！个排列σ，排列σ的“正负号"或“正负号函数”sgnσ是|1或-1，取决于由{1，2，…，n}开始到得到排列σ所需对换(或两两交换)的最小数是偶数还是奇数．于是，每个乘积

都在行列式中出现，如果 $\sigma$ 是偶排列，则在乘积前冠以 $+$ 号，如果 $\sigma$ 是奇排列，就冠以 $^{\cdot}$ 号.

如果系数 $\operatorname{sgn} \sigma$ 用某些其他的函数来代替，那么所谓的广义矩阵函数就取代了 $\det A$ 。一个例子是 per $A$ ，称为 $A$ 的积和式（permanent），其中 $\operatorname{sgn} \sigma$ 被恒等于 1 的函数所代替。

0.3.3 初等变换 有三种简单的基本变换，人们常常可以利用这些变换把任一个矩阵化简成与该矩阵相抵的、唯一简单的形式（即标准形），以便用它来解线性方程组。计算行列式，矩阵求逆和研究矩阵的秩，等等。我们集中讨论关于行的变换，它们是如下一种变换。

第一种：交换矩阵的两行

交换第 $i$ 行和第 $j$ 行可以经左乘以矩阵

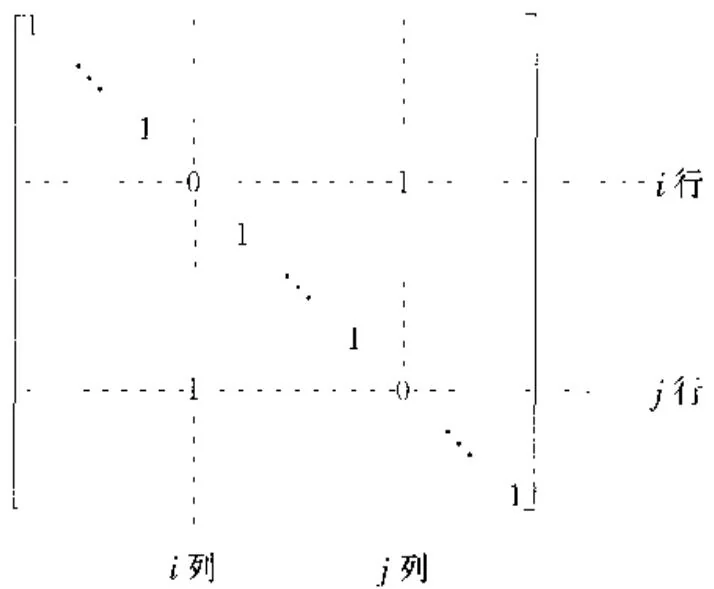
来实现，其中，在 $i$ 、 $j$ 位置和 $j$ ， $i$ 位置上的两个非对角元是1，而所有未注明的元都是0.

第二种：用一个非零纯量乘某一行

用一个纯量 $c$ 乘 $A$ 的第 $i$ 行可以经左乘以矩阵

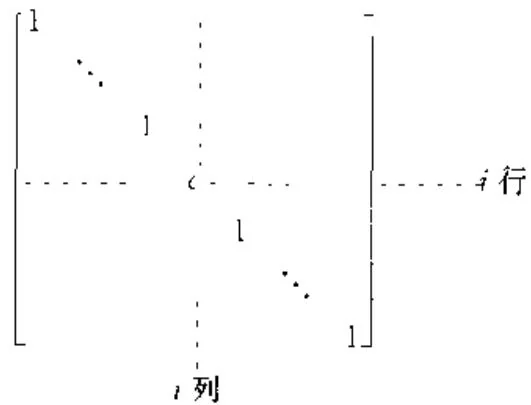
来实现，其中纯量 $i$ 出现在 $i, i$ 位置.

第三种；把某一行的纯量倍数加到另一行

用 $c$ 乘第 $i$ 行加到第 $j$ 行相当于把 $A$ 左乘以矩阵

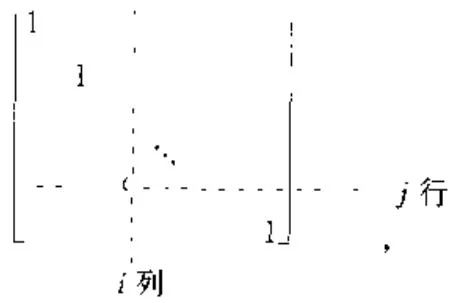
其中纯量 $\pmb{\mathcal{C}}$ 出现在 $j,i$ 位置．注意，上述每个作初等变换的矩阵，正好是把相应的初等变换施于单位矩阵 $\pmb{I}$ 的结果.

第一种初等变换在行列式上的作用是将行列式乘以 $-1$ ；第二种变换的作用是将它乘以纯量 $c$ ；第三种变换不改变行列式。由此可知，如果一个矩阵有一个零行，或有两行相关，或任意 $k$ 行相关，那么它的行列式为零。一个矩阵的行列式是零，当且仅当它的诸行的一个子集线性相关。

0.3.4 行简化梯形阵 对每个 $A \in M_{m,n}(\mathbf{F})$ ，在 $M_{m,n}(\mathbf{F})$ 中存在一个标准形， $A$ 的行简化梯形 (RREF)，它可以经（不唯一的）一系列初等变换得到。许多矩阵有相同的 RREF，每个矩阵不管经一列什么样的初等变换而得到，它只有一个 RREF。RREF 的定义是：

(a) 各非零行的第一个非零元是 1;
（b）具有上述首元1的列的所有其他元都为零；
（c）全由零元组成的行出现在矩阵的底部；
(d) 诸首元1位于从左到右的“阶梯型”之中，即下一行的首元1必须出现在其上一行的首元1的右边。例如，

是RREF. $A \in M_{n}(\mathbf{F})$ 的行列式是非零的，当且仅当它的RREF是单位矩阵

（它的行列式是1）. 记录下把 $A$ 化成RREF的每个初等变换对 $A$ 的行列式的作用，可以用来计算 $\det A$ 的值.

考虑线性方程组 $Ax = b$ ，其中 $A \in M_{m,n}(\mathbf{F})$ 和 $b \in \mathbb{F}^{m}$ 已知，而 $x \in \mathbb{F}^{n}$ 未知。对 $A$ 和 $b$ 施以相同的初等变换，解集合不变。解可以从 $[Ab]$ 的RREF看出来。事实上，RREF是唯一的，并且两个方程组 $Ax = b$ 是解等价的（有相同的解集合），当且仅当两个增广矩阵 $[Ab]$ 有相同的RREF。

后面，将讨论RREF在求矩阵的秩和逆中的作用

0.3.5 乘法性质 行列式函数最关键和最重要的性质是，它是可相乘的：对于 $A$ ， $B \in M_{n}(\mathbf{F})$ ，

用初等变换把 $A$ 和 $B$ 都行简化就可以证明这个等式.

0.3.6 行列式的函数特征 把行列式分别看成每一行(或列)的函数，而让其余各行(或列)不变，那么它是该行(或列)各元的线性函数。从 Laplace 展开式来看，这是很明显的，因为一个给定的元的系数正好是它的上余子式，而余子式是固定不变的。如果一个函数依次对其各变元的一个给定划分中的每一组变元都是线性的，就称这个函数是多重线性的。这是相当广泛的一类函数。例如，函数 $f(x_{1}, x_{2}) = x_{1}x_{2}$ 关于划分 $\{x_{1}\}, \{x_{2}\}$ 是多重线性的。又如，行列式作为矩阵的各元的函数，它对相应于各行(或列)的划分是多重线性的。

人们自然要问，是否迄今所提到的行列式的任何一组性质都把它描述成 $A \in M_n$ 的 $n^2$ 个元

[1] 的一个纯量值函数，行列式是唯一满足下列条件的函数 $f: M_{n}(\mathbf{F}) \to \mathbf{F}$

（a）多重线性的；
（b）交错的：第一种初等变换使结果乘以-1；
(c) 规范的: $f(I) = 1$ , 其中 $I \in M_{n}(\mathbf{F})$ 是单位矩阵.

积和式函数（这是另一类广义矩阵函数）也是多重线性的和规范的，但它不是交错的。