3.3 QR分解 QR分解是将一个矩阵分解一个正交矩阵(酉矩阵)和一个三角矩阵的乘积. QR分解被广泛应用于线性最小二乘问题的求解和矩阵特征值的计算.
3.3.1 QR分解的存在性与唯一性 定理3.9 (QR分解) [73] 设 A ∈ C m × n A \in \mathbb{C}^{m \times n} A ∈ C m × n m ≥ n m \geq n m ≥ n Q ∈ C m × n Q \in \mathbb{C}^{m \times n} Q ∈ C m × n Q ∗ Q = I n × n Q^{*}Q = I_{n \times n} Q ∗ Q = I n × n R ∈ C n × n R \in \mathbb{C}^{n \times n} R ∈ C n × n
A = Q R . (3.8) A = Q R. \tag {3.8} A = QR . ( 3.8 ) 若 A A A R R R Q Q Q R R R
证明. 设 A = [ a 1 , a 2 , … , a n ] ∈ C m × n A = [a_{1}, a_{2}, \ldots, a_{n}] \in \mathbb{C}^{m \times n} A = [ a 1 , a 2 , … , a n ] ∈ C m × n A A A rank ( A ) = n \operatorname{rank}(A) = n rank ( A ) = n A A A
算法3.3.Gram-Schmidt正交化过程 1: r 11 = ∥ a 1 ∥ 2 r_{11} = \left\| a_1\right\| _2 r 11 = ∥ a 1 ∥ 2 q 1 = a 1 / r 11 q_{1} = a_{1} / r_{11} q 1 = a 1 / r 11 j = 2 j = 2 j = 2 n n n q j = a j q_{j} = a_{j} q j = a j i = 1 i = 1 i = 1 j − 1 j - 1 j − 1 r i j = ( a j , q i ) % r_{ij} = (a_j, q_i) \quad \% r ij = ( a j , q i ) % q j = q j − r i j q i q_{j} = q_{j} - r_{ij}q_{i} q j = q j − r ij q i r j j = ∥ q j ∥ 2 r_{jj} = \| q_j\| _2 r jj = ∥ q j ∥ 2 q j = q j / r j j q_{j} = q_{j} / r_{jj} q j = q j / r jj
由算法3.3可知
a 1 = r 11 q 1 , a j = r 1 j q 1 + r 2 j q 2 + ⋯ + r j j q j = [ q 1 , q 2 , … , q j ] [ r 1 j r 2 j ⋮ r j j ] , j = 2 , 3 , … , n . a _ {1} = r _ {1 1} q _ {1}, \quad a _ {j} = r _ {1 j} q _ {1} + r _ {2 j} q _ {2} + \dots + r _ {j j} q _ {j} = [ q _ {1}, q _ {2}, \ldots , q _ {j} ] \left[ \begin{array}{c} r _ {1 j} \\ r _ {2 j} \\ \vdots \\ r _ {j j} \end{array} \right], \quad j = 2, 3, \ldots , n. a 1 = r 11 q 1 , a j = r 1 j q 1 + r 2 j q 2 + ⋯ + r jj q j = [ q 1 , q 2 , … , q j ] r 1 j r 2 j ⋮ r jj , j = 2 , 3 , … , n . 记 Q = [ q 1 , q 2 , … , q n ] Q = [q_{1}, q_{2}, \ldots, q_{n}] Q = [ q 1 , q 2 , … , q n ] R = [ r i j ] n × n R = [r_{ij}]_{n \times n} R = [ r ij ] n × n
r i j = { q i ∗ a j , f o r i ≤ j 0 , f o r i > j (3.9) r _ {i j} = \left\{ \begin{array}{l l} q _ {i} ^ {*} a _ {j}, & \text {f o r} i \leq j \\ 0, & \text {f o r} i > j \end{array} \right. \tag {3.9} r ij = { q i ∗ a j , 0 , f o r i ≤ j f o r i > j ( 3.9 ) 于是Gram-Schmidt正交化过程可表示为
[ a 1 , a 2 , … , a n ] = [ q 1 , q 2 , … , q n ] [ r 11 r 12 … r 1 n r 22 … r 2 n ⋱ r n − 1 , n r n n ] , 即 A = Q R . [ a _ {1}, a _ {2}, \ldots , a _ {n} ] = [ q _ {1}, q _ {2}, \ldots , q _ {n} ] \left[ \begin{array}{c c c c} {{r _ {1 1}}} & {{r _ {1 2}}} & {{\dots}} & {{r _ {1 n}}} \\ {} & {{r _ {2 2}}} & {{\dots}} & {{r _ {2 n}}} \\ {} & {} & {{\ddots}} & {{r _ {n - 1, n}}} \\ {} & {} & {} & {{r _ {n n}}} \end{array} \right], \quad \text {即} \quad A = Q R. [ a 1 , a 2 , … , a n ] = [ q 1 , q 2 , … , q n ] r 11 r 12 r 22 … … ⋱ r 1 n r 2 n r n − 1 , n r nn , 即 A = QR . 如果 A A A
如果 a 1 = 0 a_1 = 0 a 1 = 0 q 1 = 0 q_1 = 0 q 1 = 0 q 1 = a 1 / ∥ a 1 ∥ 2 q_1 = a_1 / \|a_1\|_2 q 1 = a 1 /∥ a 1 ∥ 2
对于 j = 2 , 3 , … , n j = 2,3,\ldots ,n j = 2 , 3 , … , n q ~ j = a j − ∑ i = 1 j − 1 ( q i ∗ a j ) q i \tilde{q}_j = a_j - \sum_{i = 1}^{j - 1}(q_i^* a_j)q_i q ~ j = a j − ∑ i = 1 j − 1 ( q i ∗ a j ) q i q ~ j = 0 \tilde{q}_j = 0 q ~ j = 0 a j a_{j} a j a 1 , a 2 , … , a j − 1 a_1,a_2,\dots ,a_{j - 1} a 1 , a 2 , … , a j − 1 q j = 0. q_{j} = 0. q j = 0. q j = q ~ j / ∥ q ~ j ∥ 2 q_{j} = \tilde{q}_{j} / \| \tilde{q}_{j}\|_{2} q j = q ~ j /∥ q ~ j ∥ 2
于是我们有
其中 Q = [ q 1 , q 2 , … , q n ] Q = [q_{1}, q_{2}, \ldots, q_{n}] Q = [ q 1 , q 2 , … , q n ] R = [ r i j ] n × n R = [r_{ij}]_{n \times n} R = [ r ij ] n × n Q Q Q q k = 0 q_{k} = 0 q k = 0 R R R k k k
设 rank ( A ) = l < n \operatorname{rank}(A) = l < n rank ( A ) = l < n Q Q Q l l l q i 1 , q i 2 , … , q i l q_{i_1}, q_{i_2}, \ldots, q_{i_l} q i 1 , q i 2 , … , q i l C m \mathbb{C}^m C m C m \mathbb{C}^m C m
q i 1 , q i 2 , … , q i l , q ~ 1 , … , q ~ m − l . q _ {i _ {1}}, q _ {i _ {2}}, \dots , q _ {i _ {l}}, \tilde {q} _ {1}, \dots , \tilde {q} _ {m - l}. q i 1 , q i 2 , … , q i l , q ~ 1 , … , q ~ m − l . 然后我们用 q ~ 1 \tilde{q}_1 q ~ 1 Q Q Q q ~ 2 \tilde{q}_2 q ~ 2 Q Q Q Q Q Q Q ~ \tilde{Q} Q ~ Q ~ ∈ C m × n \tilde{Q} \in \mathbb{C}^{m \times n} Q ~ ∈ C m × n
Q ~ R = Q R . \tilde {Q} R = Q R. Q ~ R = QR . 这是由于 Q ~ \tilde{Q} Q ~ R R R
A = Q ~ R . A = \tilde {Q} R. A = Q ~ R . 下面证明满秩矩阵QR分解的存在唯一性
存在性: 由于 A A A R = [ r i j ] n × n R = [r_{ij}]_{n \times n} R = [ r ij ] n × n r j j > 0 r_{jj} > 0 r jj > 0 A = Q R A = QR A = QR Q Q Q
唯一性: 假设 A A A
A = Q 1 R 1 = Q 2 R 2 , A = Q _ {1} R _ {1} = Q _ {2} R _ {2}, A = Q 1 R 1 = Q 2 R 2 , 其中 Q 1 , Q 2 ∈ C m × n Q_{1}, Q_{2} \in \mathbb{C}^{m \times n} Q 1 , Q 2 ∈ C m × n R 1 , R 2 ∈ C n × n R_{1}, R_{2} \in \mathbb{C}^{n \times n} R 1 , R 2 ∈ C n × n
Q 1 = Q 2 R 2 R 1 − 1 . (3.10) Q _ {1} = Q _ {2} R _ {2} R _ {1} ^ {- 1}. \tag {3.10} Q 1 = Q 2 R 2 R 1 − 1 . ( 3.10 ) 于是
1 = ∥ Q 1 ∥ 2 = ∥ Q 2 R 2 R 1 − 1 ∥ 2 = ∥ R 2 R 1 − 1 ∥ 2 . 1 = \| Q _ {1} \| _ {2} = \| Q _ {2} R _ {2} R _ {1} ^ {- 1} \| _ {2} = \| R _ {2} R _ {1} ^ {- 1} \| _ {2}. 1 = ∥ Q 1 ∥ 2 = ∥ Q 2 R 2 R 1 − 1 ∥ 2 = ∥ R 2 R 1 − 1 ∥ 2 . 又 R 1 , R 2 R_{1}, R_{2} R 1 , R 2 R 2 R 1 − 1 R_{2}R_{1}^{-1} R 2 R 1 − 1 R 2 ( i , i ) / R 1 ( i , i ) R_{2}(i,i) / R_{1}(i,i) R 2 ( i , i ) / R 1 ( i , i )
i = 1 , 2 , … , n . i = 1,2,\dots ,n. i = 1 , 2 , … , n .
R 2 ( i , i ) R 1 ( i , i ) ≤ ρ ( R 2 R 1 − 1 ) ≤ ∥ R 2 R 1 − 1 ∥ 2 ≤ 1 , i = 1 , 2 , … , n . \frac {R _ {2} (i , i)}{R _ {1} (i , i)} \leq \rho \left(R _ {2} R _ {1} ^ {- 1}\right) \leq \| R _ {2} R _ {1} ^ {- 1} \| _ {2} \leq 1, \quad i = 1, 2, \dots , n. R 1 ( i , i ) R 2 ( i , i ) ≤ ρ ( R 2 R 1 − 1 ) ≤ ∥ R 2 R 1 − 1 ∥ 2 ≤ 1 , i = 1 , 2 , … , n . 同理可证 R 1 ( i , i ) / R 2 ( i , i ) ≤ 1. R_{1}(i,i) / R_{2}(i,i)\leq 1. R 1 ( i , i ) / R 2 ( i , i ) ≤ 1.
R 1 ( i , i ) = R 2 ( i , i ) , i = 1 , 2 , … , n . R _ {1} (i, i) = R _ {2} (i, i), \quad i = 1, 2, \dots , n. R 1 ( i , i ) = R 2 ( i , i ) , i = 1 , 2 , … , n . 又 ∥ Q 1 ∥ F 2 = t r ( Q 1 ∗ Q 1 ) = n , \| Q_1\| _F^2 = \mathrm{tr}(Q_1^* Q_1) = n, ∥ Q 1 ∥ F 2 = tr ( Q 1 ∗ Q 1 ) = n ,
∥ R 2 R 1 − 1 ∥ F 2 = ∥ Q 2 R 2 R 1 − 1 ∥ F 2 = ∥ Q 1 ∥ F 2 = n . \| R _ {2} R _ {1} ^ {- 1} \| _ {F} ^ {2} = \| Q _ {2} R _ {2} R _ {1} ^ {- 1} \| _ {F} ^ {2} = \| Q _ {1} \| _ {F} ^ {2} = n. ∥ R 2 R 1 − 1 ∥ F 2 = ∥ Q 2 R 2 R 1 − 1 ∥ F 2 = ∥ Q 1 ∥ F 2 = n . 由于 R 2 R 1 − 1 R_{2}R_{1}^{-1} R 2 R 1 − 1 R 2 R 1 − 1 R_{2}R_{1}^{-1} R 2 R 1 − 1 R 2 = R 1 R_{2} = R_{1} R 2 = R 1 Q 2 = A R 2 − 1 = Q_{2} = AR_{2}^{-1} = Q 2 = A R 2 − 1 = A R 1 − 1 = Q 1 AR_1^{-1} = Q_1 A R 1 − 1 = Q 1 A A A
A 有时也将 QR 分解定义为: 存在酉矩阵 Q ∈ C m × m Q \in \mathbb{C}^{m \times m} Q ∈ C m × m
其中 R = [ R 11 0 ] ∈ C m × n R = \left[ \begin{array}{c} R_{11} \\ 0 \end{array} \right] \in \mathbb{C}^{m \times n} R = [ R 11 0 ] ∈ C m × n
如果 A A A Q Q Q R R R A A A A x = b Ax = b A x = b
Gram-Schmidt正交化与正交投影 Gram-Schmidt 正交化过程的第 j j j
q ~ j = a j − r 1 j q 1 − r 2 j q 2 − ⋯ − r j − 1 , j q j − 1 \tilde {q} _ {j} = a _ {j} - r _ {1 j} q _ {1} - r _ {2 j} q _ {2} - \dots - r _ {j - 1, j} q _ {j - 1} q ~ j = a j − r 1 j q 1 − r 2 j q 2 − ⋯ − r j − 1 , j q j − 1 可以看作是 a j a_{j} a j span { q 1 , q 2 , … , q j − 1 } \operatorname{span}\{q_1, q_2, \ldots, q_{j-1}\} span { q 1 , q 2 , … , q j − 1 } r i j q i r_{ij}q_i r ij q i a j a_{j} a j q i q_i q i
P s p a n { q i } a j = ( q i q i ⊺ ) a j = ( q i ⊺ a j ) q i = r i j q i . P _ {\mathrm {s p a n} \{q _ {i} \}} a _ {j} = (q _ {i} q _ {i} ^ {\intercal}) a _ {j} = (q _ {i} ^ {\intercal} a _ {j}) q _ {i} = r _ {i j} q _ {i}. P span { q i } a j = ( q i q i ⊺ ) a j = ( q i ⊺ a j ) q i = r ij q i . 下面给出QR分解的具体实现方法,分别基于MGS正交化过程, Householder变换和Givens变换.
3.3.2 基于MGS的QR分解 在证明QR分解的存在性时,我们利用了Gram-Schmidt正交化过程.但由于数值稳定性方面的原因,在实际计算中,我们一般不采用Gram-Schmidt正交化过程,取而代之的是修正的Gram-Schmidt正交化过程(modified Gram-Schmidt process,MGS),即对正交化过程做如下修改:
Gram-Schmidt 正交化过程的第 j j j
(1) 计算 r i j = ( a j , q i ) r_{ij} = (a_j, q_i) r ij = ( a j , q i ) i = 1 , 2 , … , j − 1 i = 1, 2, \ldots, j - 1 i = 1 , 2 , … , j − 1 q ~ j = a j − r 1 j q 1 − r 2 j q 2 − ⋯ − r j − 1 , j q j − 1 ; \tilde{q}_j = a_j - r_{1j}q_1 - r_{2j}q_2 - \dots -r_{j - 1,j}q_{j - 1}; q ~ j = a j − r 1 j q 1 − r 2 j q 2 − ⋯ − r j − 1 , j q j − 1 ; r j j = ∥ q ~ j ∥ r_{jj} = \|\tilde{q}_j\| r jj = ∥ q ~ j ∥ q j = q ~ j / r j j q_j = \tilde{q}_j / r_{jj} q j = q ~ j / r jj
(1) 令 q ~ j = a j \tilde{q}_j = a_j q ~ j = a j r i j = ( q ~ j , q i ) r_{ij} = (\tilde{q}_j, q_i) r ij = ( q ~ j , q i ) q ~ j = q ~ j − r i j q i \tilde{q}_j = \tilde{q}_j - r_{ij}q_i q ~ j = q ~ j − r ij q i i = 1 , 2 , … , j − 1 i = 1, 2, \ldots, j-1 i = 1 , 2 , … , j − 1 r j j = ∥ q ~ j ∥ r_{jj} = \|\tilde{q}_j\| r jj = ∥ q ~ j ∥ q j = q ~ j / r j j q_j = \tilde{q}_j / r_{jj} q j = q ~ j / r jj
可以证明, 数学上这两个算法完全等价, 即 r i j r_{ij} r ij q j q_j q j
算法3.4.基于MGS的QR分解 % \% % A ∈ C m × n A \in \mathbb{C}^{m \times n} A ∈ C m × n Q = [ q 1 , … , q n ] ∈ R m × n Q = [q_1, \ldots, q_n] \in \mathbb{R}^{m \times n} Q = [ q 1 , … , q n ] ∈ R m × n R ∈ R n × n R \in \mathbb{R}^{n \times n} R ∈ R n × n A = Q R A = QR A = QR
1: Set R = [ r i j ] = 0 n × n R = [r_{ij}] = 0_{n \times n} R = [ r ij ] = 0 n × n n × n n \times n n × n a 1 = 0 a_1 = 0 a 1 = 0 q 1 = 0 q_{1} = 0 q 1 = 0 r 11 = ∥ a 1 ∥ 2 , q 1 = a 1 / ∥ a 1 ∥ 2 r_{11} = \| a_1\| _2, \quad q_1 = a_1 / \| a_1\| _2 r 11 = ∥ a 1 ∥ 2 , q 1 = a 1 /∥ a 1 ∥ 2 j = 2 j = 2 j = 2 n n n q j = a j q_{j} = a_{j} q j = a j i = 1 i = 1 i = 1 j − 1 j - 1 j − 1 % \% % r i j = ( q j , q i ) , q j = q j − r i j q i r_{ij} = (q_j,q_i),\quad q_j = q_j - r_{ij}q_i r ij = ( q j , q i ) , q j = q j − r ij q i q j ≠ 0 q_{j}\neq 0 q j = 0 r j j = ∥ q j ∥ 2 , q j = q j / r j j r_{jj} = \| q_j\| _2, \quad q_j = q_j / r_{jj} r jj = ∥ q j ∥ 2 , q j = q j / r jj
A 本算法的运算量大约为 2 m n 2 2mn^{2} 2 m n 2 R R R Q ∈ R m × n , R ∈ R n × n Q\in \mathbb{R}^{m\times n},R\in \mathbb{R}^{n\times n} Q ∈ R m × n , R ∈ R n × n
3.3.3 基于Householder变换的QR分解 由定理3.5可知, 通过Householder变换, 我们可以将任何一个非零变量 x ∈ R n x \in \mathbb{R}^n x ∈ R n ∥ x ∥ 2 e 1 \| x\|_2e_1 ∥ x ∥ 2 e 1
设 A ∈ R m × n A \in \mathbb{R}^{m \times n} A ∈ R m × n m ≥ n m \geq n m ≥ n H 1 ∈ R m × m H_1 \in \mathbb{R}^{m \times m} H 1 ∈ R m × m
H 1 [ a 11 a 21 ⋮ a m 1 ] = [ r 1 0 ⋮ 0 ] . H _ {1} \left[ \begin{array}{c} a _ {1 1} \\ a _ {2 1} \\ \vdots \\ a _ {m 1} \end{array} \right] = \left[ \begin{array}{c} r _ {1} \\ 0 \\ \vdots \\ 0 \end{array} \right]. H 1 a 11 a 21 ⋮ a m 1 = r 1 0 ⋮ 0 . 于是
H 1 A = [ r 1 a ~ 12 … a ~ 1 n 0 ⋮ A ~ 2 0 ] , H _ {1} A = \left[ \begin{array}{c c c c} r _ {1} & \tilde {a} _ {1 2} & \dots & \tilde {a} _ {1 n} \\ \hline 0 & & \\ \vdots & & \tilde {A} _ {2} \\ 0 & & \end{array} \right], H 1 A = r 1 0 ⋮ 0 a ~ 12 … A ~ 2 a ~ 1 n , 其中 A ~ 2 ∈ R ( m − 1 ) × ( n − 1 ) \tilde{A}_2\in \mathbb{R}^{(m - 1)\times (n - 1)} A ~ 2 ∈ R ( m − 1 ) × ( n − 1 ) H ~ 2 ∈ R ( m − 1 ) × ( m − 1 ) \tilde{H}_2\in \mathbb{R}^{(m - 1)\times (m - 1)} H ~ 2 ∈ R ( m − 1 ) × ( m − 1 ) A ~ 2 \tilde{A}_2 A ~ 2
H ~ 2 A ~ 2 = [ r 2 a ~ 23 … a ~ 2 n 0 ⋮ A ~ 3 0 ] . \tilde {H} _ {2} \tilde {A} _ {2} = \left[ \begin{array}{c c c c} r _ {2} & \tilde {a} _ {2 3} & \dots & \tilde {a} _ {2 n} \\ \hline 0 & & \\ \vdots & & \tilde {A} _ {3} \\ 0 & & \end{array} \right]. H ~ 2 A ~ 2 = r 2 0 ⋮ 0 a ~ 23 … A ~ 3 a ~ 2 n . 令 H 2 = [ 1 0 0 H ~ 2 ] H_{2} = \left[ \begin{array}{cc}1 & 0\\ 0 & \tilde{H}_{2} \end{array} \right] H 2 = [ 1 0 0 H ~ 2 ] H 2 ∈ R m × m H_{2}\in \mathbb{R}^{m\times m} H 2 ∈ R m × m
H 2 H 1 A = [ r 1 a ~ 12 a ~ 13 … a ~ 1 n 0 r 2 a ~ 23 … a ~ 2 n 0 0 ⋮ ⋮ A ~ 3 0 0 ] . H _ {2} H _ {1} A = \left[ \begin{array}{c c c c c} r _ {1} & \tilde {a} _ {1 2} & \tilde {a} _ {1 3} & \dots & \tilde {a} _ {1 n} \\ 0 & r _ {2} & \tilde {a} _ {2 3} & \dots & \tilde {a} _ {2 n} \\ \hline 0 & 0 & & & \\ \vdots & \vdots & & \tilde {A} _ {3} \\ 0 & 0 & & & \end{array} \right]. H 2 H 1 A = r 1 0 0 ⋮ 0 a ~ 12 r 2 0 ⋮ 0 a ~ 13 a ~ 23 … … A ~ 3 a ~ 1 n a ~ 2 n . 不断重复上述过程, 我们就可以得到一系列的 Householder 变换
H k = [ I k − 1 0 0 H ~ k ] , H ~ k ∈ R ( n + 1 − k ) × ( n + 1 − k ) , k = 1 , 2 , … , n , H _ {k} = \left[ \begin{array}{c c} I _ {k - 1} & 0 \\ 0 & \tilde {H} _ {k} \end{array} \right], \quad \tilde {H} _ {k} \in \mathbb {R} ^ {(n + 1 - k) \times (n + 1 - k)}, \quad k = 1, 2, \ldots , n, H k = [ I k − 1 0 0 H ~ k ] , H ~ k ∈ R ( n + 1 − k ) × ( n + 1 − k ) , k = 1 , 2 , … , n , 使得
H n … H 2 H 1 A = [ r 1 a ~ 12 … a ~ 1 n 0 r 2 … a ~ 2 n ⋮ ⋱ ⋮ 0 0 … r n 0 0 … 0 ⋮ ⋮ ⋮ 0 0 … 0 ] ≜ R . H _ {n} \dots H _ {2} H _ {1} A = \left[ \begin{array}{c c c c} r _ {1} & \tilde {a} _ {1 2} & \dots & \tilde {a} _ {1 n} \\ 0 & r _ {2} & \dots & \tilde {a} _ {2 n} \\ \vdots & & \ddots & \vdots \\ 0 & 0 & \dots & r _ {n} \\ 0 & 0 & \dots & 0 \\ \vdots & \vdots & & \vdots \\ 0 & 0 & \dots & 0 \end{array} \right] \triangleq R. H n … H 2 H 1 A = r 1 0 ⋮ 0 0 ⋮ 0 a ~ 12 r 2 0 0 ⋮ 0 … … ⋱ … … … a ~ 1 n a ~ 2 n ⋮ r n 0 ⋮ 0 ≜ R . 由于Householder变换都是正交矩阵,令
Q ≜ ( H n … H 2 H 1 ) − 1 = H 1 − 1 H 2 − 1 … H n − 1 = H 1 H 2 … H n , Q \triangleq \left(H _ {n} \dots H _ {2} H _ {1}\right) ^ {- 1} = H _ {1} ^ {- 1} H _ {2} ^ {- 1} \dots H _ {n} ^ {- 1} = H _ {1} H _ {2} \dots H _ {n}, Q ≜ ( H n … H 2 H 1 ) − 1 = H 1 − 1 H 2 − 1 … H n − 1 = H 1 H 2 … H n , 则 Q Q Q
A = ( H n − 1 ⋅ ⋅ ⋅ H 2 H 1 ) − 1 R = Q R . A = (H _ {n - 1} \cdot \cdot \cdot H _ {2} H _ {1}) ^ {- 1} R = Q R. A = ( H n − 1 ⋅ ⋅ ⋅ H 2 H 1 ) − 1 R = QR . 以上就是基于Householder变换的QR分解的具体实现过程.最后所得到的上三角矩阵 R R R A A A
如果不需要生成 Q Q Q 2 m n 2 − 2 n 3 / 3 2mn^{2} - 2n^{3}/3 2 m n 2 − 2 n 3 /3
矩阵 Q Q Q
{ Q = I m , Q = Q H k , k = 1 , 2 , … , n . \left\{ \begin{array}{l} Q = I _ {m}, \\ Q = Q H _ {k}, \quad k = 1, 2, \ldots , n. \end{array} \right. { Q = I m , Q = Q H k , k = 1 , 2 , … , n . 如果保留了每一步的Householder向量, 则 Q Q Q
Q = H k Q , k = n , n − 1 , … , 1. Q = H _ {k} Q, \quad k = n, n - 1, \dots , 1. Q = H k Q , k = n , n − 1 , … , 1. 这样做的好处是一开始 Q Q Q Q Q Q Q Q Q
采用向后累积方法计算 Q Q Q 4 m 2 n − 4 m n 2 + 4 n 3 / 3 4m^{2}n - 4mn^{2} + 4n^{3} / 3 4 m 2 n − 4 m n 2 + 4 n 3 /3 Q Q Q n n n 2 m n 2 − 2 n 3 / 3 2mn^{2} - 2n^{3} / 3 2 m n 2 − 2 n 3 /3 4 m n 2 − 4 n 3 / 3 4mn^{2} - 4n^{3} / 3 4 m n 2 − 4 n 3 /3 m = n m = n m = n 8 n 3 / 3 8n^{3} / 3 8 n 3 /3
算法3.5.基于Householder变换的QR分解 % \% % A ∈ R m × n A \in \mathbb{R}^{m \times n} A ∈ R m × n Q Q Q R R R A = Q R A = QR A = QR Q ∈ R m × m Q \in \mathbb{R}^{m \times m} Q ∈ R m × m R ∈ R m × n R \in \mathbb{R}^{m \times n} R ∈ R m × n % \% % R R R A A A
1: Set Q = I m × m Q = I_{m \times m} Q = I m × m k = 1 k = 1 k = 1 n n n x = A ( k : m , k ) x = A(k:m,k) x = A ( k : m , k ) [ β k , v k ] = H o u s e ( x ) [\beta_k, v_k] = \mathbf{House}(x) [ β k , v k ] = House ( x ) A ( k : m , k : n ) = ( I m − k + 1 − β k v k v k ⊤ ) A ( k : m , k : n ) A(k:m,k:n) = (I_{m - k + 1} - \beta_kv_kv_k^\top)A(k:m,k:n) A ( k : m , k : n ) = ( I m − k + 1 − β k v k v k ⊤ ) A ( k : m , k : n ) = A ( k : m , k : n ) − β k v k ( v k T A ( k : m , k : n ) ) = A(k:m,k:n) - \beta_{k}v_{k}\big(v_{k}^{\mathsf{T}}A(k:m,k:n)\big) = A ( k : m , k : n ) − β k v k ( v k T A ( k : m , k : n ) ) Q ( : , k : m ) = Q ( : , k : m ) ( I m − k + 1 − β k v k v k ⊤ ) Q(:, k : m) = Q(:, k : m)(I_{m-k+1} - \beta_k v_k v_k^\top) Q ( : , k : m ) = Q ( : , k : m ) ( I m − k + 1 − β k v k v k ⊤ ) = Q ( : , k : m ) − β k ( Q ( : , k : m ) v k ) v k T = Q(:,k:m) - \beta_{k}\big(Q(:,k:m)v_{k}\big)v_{k}^{\mathsf{T}} = Q ( : , k : m ) − β k ( Q ( : , k : m ) v k ) v k T
上面的算法只是关于Householder QR分解的一个简单描述,并没有考虑运算量问题.在实际计算时,我们通常会保留所有的Householder向量(用于向后累积法计算 Q Q Q k k k H ~ k \tilde{H}_k H ~ k v k v_{k} v k m − k + 1 m - k + 1 m − k + 1 v k v_{k} v k v k v_{k} v k v k ( 2 : e n d ) v_{k}(2:end) v k ( 2 : e n d ) m − k m - k m − k
Householder 向量存放在 A A A A A A R R R
事实上, 如果没有明确要求生成 Q Q Q v k v_{k} v k β k \beta_{k} β k Q Q Q
我们也可以考虑块Householder QR分解,以便充分利用3级BLAS运算,提高计算效率.
3.3.4 列主元QR分解 如果 A A A l ≜ rank ( A ) < n l \triangleq \operatorname{rank}(A) < n l ≜ rank ( A ) < n P P P A P AP A P l l l A P AP A P
定理3.10 (列主元QR分解) 设 A ∈ C m × n A \in \mathbb{C}^{m \times n} A ∈ C m × n m ≥ n m \geq n m ≥ n rank ( A ) = l < n \operatorname{rank}(A) = l < n rank ( A ) = l < n P P P Q ∈ C m × m Q \in \mathbb{C}^{m \times m} Q ∈ C m × m
A P = Q [ R 11 R 12 0 0 ] m × n , A P = Q \left[ \begin{array}{c c} R _ {1 1} & R _ {1 2} \\ 0 & 0 \end{array} \right] _ {m \times n}, A P = Q [ R 11 0 R 12 0 ] m × n , 其中 R 11 ∈ C l × l R_{11}\in \mathbb{C}^{l\times l} R 11 ∈ C l × l r 11 ≥ r 22 ≥ ⋯ ≥ r l l > 0 r_{11}\geq r_{22}\geq \dots \geq r_{ll} > 0 r 11 ≥ r 22 ≥ ⋯ ≥ r ll > 0
A 上述结论也可简化为
A P = Q 1 [ R 11 R 12 ] , A P = Q _ {1} \left[ \begin{array}{c c} R _ {1 1} & R _ {1 2} \end{array} \right], A P = Q 1 [ R 11 R 12 ] , 其中 Q 1 ∈ C m × l Q_{1}\in \mathbb{C}^{m\times l} Q 1 ∈ C m × l Q Q Q l l l
列主元QR分解的实现过程与QR分解基本类似,只是在第 k k k
假设经过 k − 1 k - 1 k − 1
A P ( k − 1 ) = Q ( k − 1 ) [ R 11 ( k − 1 ) R 12 ( k − 1 ) 0 R 22 ( k − 1 ) ] ≜ Q ( k − 1 ) R ( k − 1 ) , 即 ( Q ( k − 1 ) ) T A P ( k − 1 ) = R ( k − 1 ) , A P ^ {(k - 1)} = Q ^ {(k - 1)} \left[ \begin{array}{c c} {{R _ {1 1} ^ {(k - 1)}}} & {{R _ {1 2} ^ {(k - 1)}}} \\ {{0}} & {{R _ {2 2} ^ {(k - 1)}}} \end{array} \right] \triangleq Q ^ {(k - 1)} R ^ {(k - 1)}, \quad \text {即} \quad \left(Q ^ {(k - 1)}\right) ^ {\mathsf {T}} A P ^ {(k - 1)} = R ^ {(k - 1)}, A P ( k − 1 ) = Q ( k − 1 ) [ R 11 ( k − 1 ) 0 R 12 ( k − 1 ) R 22 ( k − 1 ) ] ≜ Q ( k − 1 ) R ( k − 1 ) , 即 ( Q ( k − 1 ) ) T A P ( k − 1 ) = R ( k − 1 ) , 其中 P ( k − 1 ) P^{(k - 1)} P ( k − 1 ) Q ( k − 1 ) Q^{(k - 1)} Q ( k − 1 ) R 11 ( k − 1 ) ∈ R ( k − 1 ) × ( k − 1 ) R_{11}^{(k - 1)}\in \mathbb{R}^{(k - 1)\times (k - 1)} R 11 ( k − 1 ) ∈ R ( k − 1 ) × ( k − 1 )
下面考虑第 k k k
(1) 首先计算 R 22 ( k − 1 ) R_{22}^{(k - 1)} R 22 ( k − 1 ) R 22 ( k − 1 ) = 0 R_{22}^{(k - 1)} = 0 R 22 ( k − 1 ) = 0 k − 1 = l k - 1 = l k − 1 = l k ≤ l k \leq l k ≤ l R 22 ( k − 1 ) ≠ 0 R_{22}^{(k-1)} \neq 0 R 22 ( k − 1 ) = 0 i k i_k i k i k ≠ 1 i_k \neq 1 i k = 1 R ( k − 1 ) R^{(k-1)} R ( k − 1 ) k k k i k + k − 1 i_k + k - 1 i k + k − 1 P k P_k P k R ( k − 1 ) R^{(k - 1)} R ( k − 1 ) k − 1 k - 1 k − 1
R ( k − 1 ) P k ≜ [ R 11 ( k − 1 ) R ~ 12 ( k − 1 ) 0 R ~ 22 ( k − 1 ) ] . R ^ {(k - 1)} P _ {k} \triangleq \left[ \begin{array}{c c} R _ {1 1} ^ {(k - 1)} & \tilde {R} _ {1 2} ^ {(k - 1)} \\ 0 & \tilde {R} _ {2 2} ^ {(k - 1)} \end{array} \right]. R ( k − 1 ) P k ≜ [ R 11 ( k − 1 ) 0 R ~ 12 ( k − 1 ) R ~ 22 ( k − 1 ) ] . 构造 R ~ 22 ( k − 1 ) \tilde{R}_{22}^{(k - 1)} R ~ 22 ( k − 1 ) H ~ k \tilde{H}_k H ~ k H k = [ I k − 1 0 0 H ~ k ] , P ( k ) = P ( k − 1 ) P k , H_{k} = \left[ \begin{array}{cc}I_{k - 1} & 0\\ 0 & \tilde{H}_{k} \end{array} \right],P^{(k)} = P^{(k - 1)}P_k, H k = [ I k − 1 0 0 H ~ k ] , P ( k ) = P ( k − 1 ) P k ,
H k ( Q ( k − 1 ) ) T A P ( k ) = H k R ( k − 1 ) P k = [ R 11 ( k − 1 ) R ~ 12 ( k − 1 ) 0 H ~ k R ~ 22 ( k − 1 ) ] ≜ R ( k ) , H _ {k} \left(Q ^ {(k - 1)}\right) ^ {\mathsf {T}} A P ^ {(k)} = H _ {k} R ^ {(k - 1)} P _ {k} = \left[ \begin{array}{c c} R _ {1 1} ^ {(k - 1)} & \tilde {R} _ {1 2} ^ {(k - 1)} \\ 0 & \tilde {H} _ {k} \tilde {R} _ {2 2} ^ {(k - 1)} \end{array} \right] \triangleq R ^ {(k)}, H k ( Q ( k − 1 ) ) T A P ( k ) = H k R ( k − 1 ) P k = [ R 11 ( k − 1 ) 0 R ~ 12 ( k − 1 ) H ~ k R ~ 22 ( k − 1 ) ] ≜ R ( k ) , 其中 H ~ k R ~ 22 ( k − 1 ) \tilde{H}_k\tilde{R}_{22}^{(k - 1)} H ~ k R ~ 22 ( k − 1 ) R ~ 22 ( k − 1 ) \tilde{R}_{22}^{(k - 1)} R ~ 22 ( k − 1 ) Q ( k ) ≜ Q ( k − 1 ) H k T Q^{(k)}\triangleq Q^{(k - 1)}H_k^{\mathsf{T}} Q ( k ) ≜ Q ( k − 1 ) H k T
A P ( k ) = Q ( k ) R ( k ) = [ R 11 ( k ) R 12 ( k ) 0 R 22 ( k ) ] , A P ^ {(k)} = Q ^ {(k)} R ^ {(k)} = \left[ \begin{array}{c c} R _ {1 1} ^ {(k)} & R _ {1 2} ^ {(k)} \\ 0 & R _ {2 2} ^ {(k)} \end{array} \right], A P ( k ) = Q ( k ) R ( k ) = [ R 11 ( k ) 0 R 12 ( k ) R 22 ( k ) ] , 其中 R 11 ( k ) ∈ R k × k R_{11}^{(k)}\in \mathbb{R}^{k\times k} R 11 ( k ) ∈ R k × k
依此类推, 直到第 l l l A A A R 11 R_{11} R 11
下面是列主元 QR 分解的一个应用.
推论3.11 (满秩分解) 设 A ∈ C m × n A \in \mathbb{C}^{m \times n} A ∈ C m × n rank ( A ) = r ≤ min { m , n } \operatorname{rank}(A) = r \leq \min\{m, n\} rank ( A ) = r ≤ min { m , n } F ∈ C m × r F \in \mathbb{C}^{m \times r} F ∈ C m × r G ∈ C r × n G \in \mathbb{C}^{r \times n} G ∈ C r × n
3.3.5 基于Givens变换的QR分解 我们同样可以利用Givens变换来做QR分解
设 A ∈ R n × n A \in \mathbb{R}^{n \times n} A ∈ R n × n G 21 G_{21} G 21 A A A
G 21 [ a 11 a 21 a 31 ⋮ a n 1 ] = [ a ~ 11 0 a 31 ⋮ a n 1 ] . G _ {2 1} \left[ \begin{array}{c} a _ {1 1} \\ a _ {2 1} \\ a _ {3 1} \\ \vdots \\ a _ {n 1} \end{array} \right] = \left[ \begin{array}{c} \tilde {a} _ {1 1} \\ 0 \\ a _ {3 1} \\ \vdots \\ a _ {n 1} \end{array} \right]. G 21 a 11 a 21 a 31 ⋮ a n 1 = a ~ 11 0 a 31 ⋮ a n 1 . 由于 G 21 G_{21} G 21 G 31 G_{31} G 31 G 21 A G_{21}A G 21 A G 31 G_{31} G 31 G 41 , G 51 , … , G n 1 G_{41}, G_{51}, \ldots, G_{n1} G 41 , G 51 , … , G n 1 G n 1 ⋯ G 21 A G_{n1} \cdots G_{21}A G n 1 ⋯ G 21 A
G n 1 … G 21 A = [ ∗ ∗ … ∗ 0 ∗ … ∗ ⋮ ⋮ ⋮ 0 ∗ … ∗ ] . G _ {n 1} \dots G _ {2 1} A = \left[ \begin{array}{c c c c} * & * & \dots & * \\ 0 & * & \dots & * \\ \vdots & \vdots & & \vdots \\ 0 & * & \dots & * \end{array} \right]. G n 1 … G 21 A = ∗ 0 ⋮ 0 ∗ ∗ ⋮ ∗ … … … ∗ ∗ ⋮ ∗ . 下面我们可以对第二列进行类似的处理.构造Givens变换 G 32 , G 42 , … , G n 2 G_{32},G_{42},\ldots ,G_{n2} G 32 , G 42 , … , G n 2 n _n n
以此类推, 我们对其他列也做类似的处理. 最后, 通过构造 1 2 n ( n − 1 ) \frac{1}{2} n(n - 1) 2 1 n ( n − 1 ) A A A
化成一个上三角矩阵 R R R
R = G n , n − 1 … G 21 A . R = G _ {n, n - 1} \dots G _ {2 1} A. R = G n , n − 1 … G 21 A . 令 Q = ( G n , n − 1 … G 21 ) T Q = (G_{n,n - 1}\dots G_{21})^{\mathsf{T}} Q = ( G n , n − 1 … G 21 ) T Q Q Q A A A
与Householder变换一样,在进行Givens变换时,我们不需要显式地写出Givens矩阵.
对于稠密矩阵而言, 基于Givens变换的QR分解的运算量比Householder变换要多很多.A ∈ R m × n A \in \mathbb{R}^{m \times n} A ∈ R m × n m > n m > n m > n
下面是基于Givens变换的QR分解的算法描述
算法3.6.基于Givens变换的QR分解 % \% % A ∈ R m × n A \in \mathbb{R}^{m \times n} A ∈ R m × n Q Q Q R R R A = Q R A = QR A = QR Q ∈ R m × m Q \in \mathbb{R}^{m \times m} Q ∈ R m × m R ∈ R m × n R \in \mathbb{R}^{m \times n} R ∈ R m × n
% \% % R R R A A A
1: Set Q = I m × m Q = I_{m \times m} Q = I m × m k = 1 k = 1 k = 1 n n n i = k + 1 i = k + 1 i = k + 1 m m m [ c , s ] = givens ( a k k , a i k ) [c, s] = \text{givens}(a_{kk}, a_{ik}) [ c , s ] = givens ( a kk , a ik ) [ A ( k , k : n ) A ( i , k : n ) ] = G [ A ( k , k : n ) A ( i , k : n ) ] \begin{bmatrix} A(k,k:n)\\ A(i,k:n) \end{bmatrix} = G\begin{bmatrix} A(k,k:n)\\ A(i,k:n) \end{bmatrix} [ A ( k , k : n ) A ( i , k : n ) ] = G [ A ( k , k : n ) A ( i , k : n ) ] G = [ c s − s c ] G = \begin{bmatrix} c & s\\ -s & c \end{bmatrix} G = [ c − s s c ] [ Q ( 1 : m , k ) , Q ( 1 : m , i ) ] = [ Q ( 1 : m , k ) , Q ( 1 : m , i ) ] G T [Q(1:m,k),Q(1:m,i)] = [Q(1:m,k),Q(1:m,i)]G^{\mathsf{T}} [ Q ( 1 : m , k ) , Q ( 1 : m , i )] = [ Q ( 1 : m , k ) , Q ( 1 : m , i )] G T
3.3.6 QR分解的稳定性 基于Householder变换和Givens变换的QR分解都具有很好的数值稳定性.详细分析可以参考[135]和[70].基于MGS的QR分解也是向后稳定的,参见[98].
当需要计算矩阵 Q Q Q A A A Q Q Q A A A
但是, 由于舍入误差的原因, 最后得到的矩阵 Q Q Q Q Q Q Q Q Q
Q T Q = I + E M G S 其 中 ∥ E M G S ∥ 2 = c 1 ( m , n ) ε u κ 2 ( A ) 1 − c 1 ( m , n ) ε u κ 2 ( A ) , Q ^ {\mathsf {T}} Q = I + E _ {M G S} \quad \text {其 中} \quad \| E _ {M G S} \| _ {2} = \frac {c _ {1} (m , n) \varepsilon_ {u} \kappa_ {2} (A)}{1 - c _ {1} (m , n) \varepsilon_ {u} \kappa_ {2} (A)}, Q T Q = I + E MGS 其 中 ∥ E MGS ∥ 2 = 1 − c 1 ( m , n ) ε u κ 2 ( A ) c 1 ( m , n ) ε u κ 2 ( A ) , 其中 c 1 ( m , n ) c_{1}(m,n) c 1 ( m , n ) m , n m,n m , n
而通过Householder变换计算的矩阵 Q Q Q
Q T Q = I + E H 其 中 ∥ E H ∥ 2 ≈ ε u . Q ^ {\mathsf {T}} Q = I + E _ {H} \quad \text {其 中} \quad \| E _ {H} \| _ {2} \approx \varepsilon_ {u}. Q T Q = I + E H 其 中 ∥ E H ∥ 2 ≈ ε u . 因此, 如果正交性至关重要, 则当 A A A
另外, 基于MGS的QR分解所计算得到的 Q Q Q Q Q Q R R R
∥ A − Q R ∥ ≈ ∥ A ∥ 2 ε u , ( ∥ A − Q R ∥ ≤ c 2 ( m , n ) ∥ A ∥ 2 ε u ) \| A - Q R \| \approx \| A \| _ {2} \varepsilon_ {u}, \quad (\| A - Q R \| \leq c _ {2} (m, n) \| A \| _ {2} \varepsilon_ {u}) ∥ A − QR ∥ ≈ ∥ A ∥ 2 ε u , ( ∥ A − QR ∥ ≤ c 2 ( m , n ) ∥ A ∥ 2 ε u ) 而且存在单位列正交矩阵 Q ~ \tilde{Q} Q ~
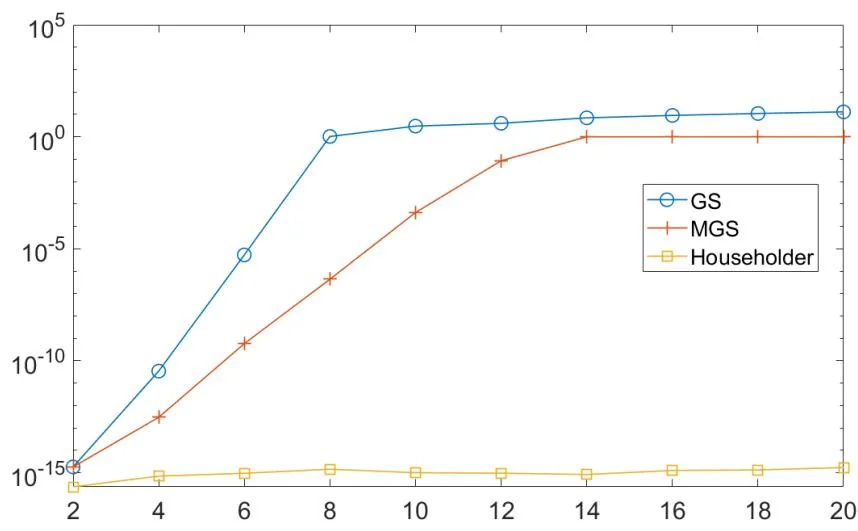
∥ A − Q ~ R ∥ ≈ ∥ A ∥ 2 ε u . \left\| A - \tilde {Q} R \right\| \approx \left\| A \right\| _ {2} \varepsilon_ {u}. A − Q ~ R ≈ ∥ A ∥ 2 ε u . 例3.3 编写程序, 分别用GS, MGS和Householder变换计算 n n n H H H ∥ Q ~ R ~ − H ∥ 2 \| \tilde{Q}\tilde{R} - H\|_2 ∥ Q ~ R ~ − H ∥ 2 ∥ Q ~ T Q ~ − I ∥ 2 \|\tilde{Q}^{\mathsf{T}}\tilde{Q} - I\|_2 ∥ Q ~ T Q ~ − I ∥ 2 Q ~ \tilde{Q} Q ~ R ~ \tilde{R} R ~
也可以通过重正交来提升MGS的稳定性,即进行两次MGS.
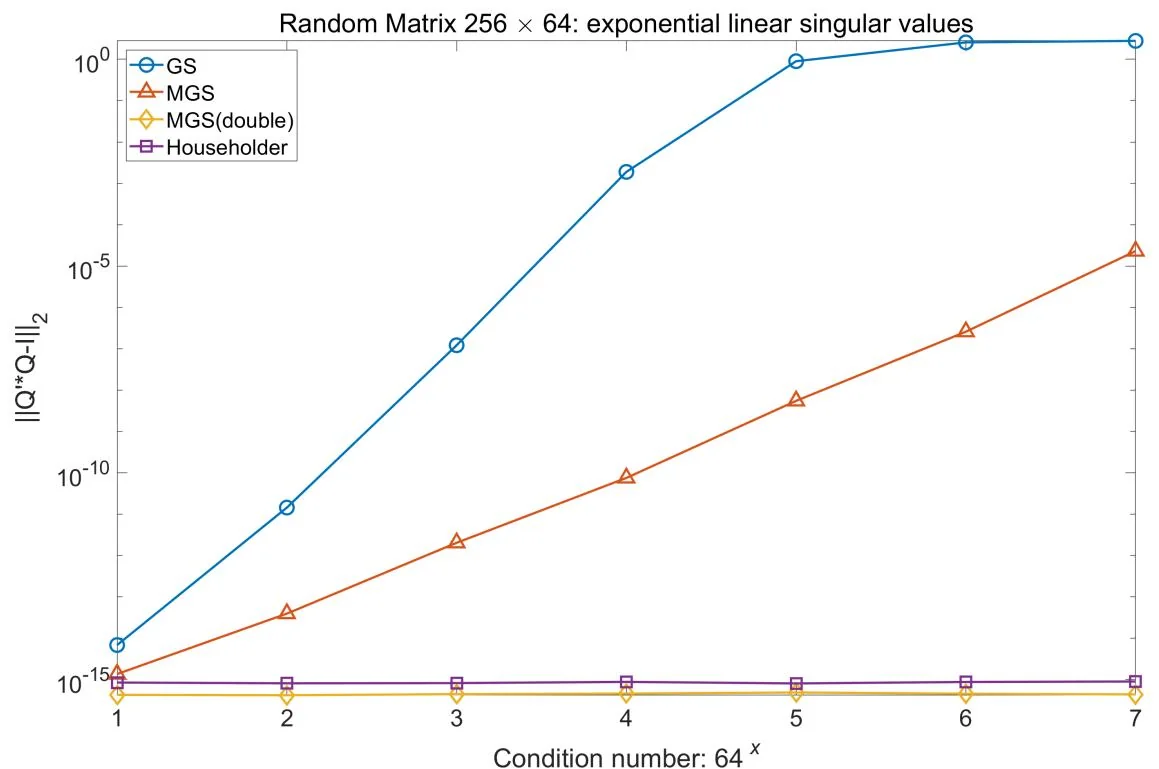
例3.4 编写程序, 分别用 GS, MGS, 两次 MGS 和 Householder 变换计算 QR 分解. 下面是针对 256 的随机矩阵, 在不同条件数下各种方法的稳定性, 试验结果如下, 其中 MGS(double) 是指两次 MGS. (QR_3methods_MGS2.m, QR_3methods_256_64.m)