3.2 几类重要的矩阵变换 矩阵计算的一个基本思想就是把复杂的问题转化为等价的且易于求解的问题. 完成这个转化的基本工具就是矩阵变换, 除了高等代数 (或线性代数) 中提到的三类初等变换以外, 在矩阵计算中常用的矩阵变换还有: Gauss 变换, Householder 变换和 Givens 变换, 其中 Gauss 变换主要用于矩阵的 LU 分解, Householder 变换和 Givens 变换是正交变换, 可用于计算线性最小二乘问题、矩阵特征值和奇异值问题等.
3.2.1 初等矩阵变换 本科高等代数教材中介绍了三类初等矩阵变换, 这里将其推广到更一般的情形. 我们称
E ( u , v , τ ) = I − τ u v ∗ (3.3) E (u, v, \tau) = I - \tau u v ^ {*} \tag {3.3} E ( u , v , τ ) = I − τu v ∗ ( 3.3 ) 为初等矩阵变换或初等矩阵, 其中 u , v ∈ C n u, v \in \mathbb{C}^n u , v ∈ C n τ \tau τ
高等代数中介绍的三类初等变换 (elementary transformation) 分别是 (以行变换为例): (1) 交换两行; (2) 某行乘以一个非零常数; (3) 某行乘以一个常数后加到另外一行. 这三类变换所对应的矩阵为 (简单示例)
E 1 = [ 1 ⋱ 0 1 ⋱ 0 ⋱ 1 ] , E 2 = [ 1 ⋱ 1 c 1 ⋱ 1 ] , E 3 = [ 1 ⋱ 1 c ⋱ 1 ⋱ 1 ] . E _ {1} = \left[ \begin{array}{c c c c c} 1 & & & & \\ & \ddots & & & \\ & & 0 & 1 & \\ & & \ddots & 0 & \\ & & & \ddots & 1 \end{array} \right], E _ {2} = \left[ \begin{array}{c c c c c} 1 & & & & \\ & \ddots & 1 & & \\ & & c & & \\ & & & 1 & \\ & & & \ddots & 1 \end{array} \right], E _ {3} = \left[ \begin{array}{c c c c c} 1 & & & & \\ & \ddots & & \\ & & 1 & & \\ & & c & \ddots & 1 \\ & & & & \ddots & 1 \end{array} \right]. E 1 = 1 ⋱ 0 ⋱ 1 0 ⋱ 1 , E 2 = 1 ⋱ 1 c 1 ⋱ 1 , E 3 = 1 ⋱ 1 c ⋱ 1 ⋱ 1 . 可以验证, 它们都可以表示为 (3.3) 形式, 留作练习
下面的定理给出了初等矩阵的基本性质
定理3.1 设 E ( u , v , τ ) E(u,v,\tau) E ( u , v , τ )
(1) det ( E ( u , v , τ ) ) = 1 − τ v ∗ u \operatorname{det}(E(u, v, \tau)) = 1 - \tau v^* u det ( E ( u , v , τ )) = 1 − τ v ∗ u 1 − τ v ∗ u ≠ 0 1 - \tau v^{*}u\neq 0 1 − τ v ∗ u = 0 E ( u , v , τ ) E(u,v,\tau) E ( u , v , τ )
( E ( u , v , τ ) ) − 1 = E ( u , v , γ ) , 其 中 γ = τ τ v ∗ u − 1 . (E (u, v, \tau)) ^ {- 1} = E (u, v, \gamma), \quad \text {其 中} \gamma = {\frac {\tau}{\tau v ^ {*} u - 1}}. ( E ( u , v , τ ) ) − 1 = E ( u , v , γ ) , 其 中 γ = τ v ∗ u − 1 τ . (3) 对任意非零向量 x , y ∈ C n x, y \in \mathbb{C}^n x , y ∈ C n u , v ∈ C n u, v \in \mathbb{C}^n u , v ∈ C n τ ∈ C \tau \in \mathbb{C} τ ∈ C
E ( u , v , τ ) x = y . E (u, v, \tau) x = y. E ( u , v , τ ) x = y . (板书)
证明. (1) 易知
[ I 0 v ∗ 1 ] [ I − τ u v ∗ − τ u 0 1 ] [ I 0 − v ∗ 1 ] = [ I − τ u 0 1 − τ v ∗ u ] . \left[ \begin{array}{c c} I & 0 \\ v ^ {*} & 1 \end{array} \right] \left[ \begin{array}{c c} I - \tau u v ^ {*} & - \tau u \\ 0 & 1 \end{array} \right] \left[ \begin{array}{c c} I & 0 \\ - v ^ {*} & 1 \end{array} \right] = \left[ \begin{array}{c c} I & - \tau u \\ 0 & 1 - \tau v ^ {*} u \end{array} \right]. [ I v ∗ 0 1 ] [ I − τu v ∗ 0 − τu 1 ] [ I − v ∗ 0 1 ] = [ I 0 − τu 1 − τ v ∗ u ] . 由行列式的乘法可知
det ( [ I 0 v ∗ 1 ] ) ⋅ det ( [ I − τ u v ∗ − τ u 0 1 ] ) ⋅ det ( [ I 0 − v ∗ 1 ] ) = det ( [ I − τ u 0 1 − τ v ∗ u ] ) . \det \left(\left[ \begin{array}{c c} I & 0 \\ v ^ {*} & 1 \end{array} \right]\right) \cdot \det \left(\left[ \begin{array}{c c} I - \tau u v ^ {*} & - \tau u \\ 0 & 1 \end{array} \right]\right) \cdot \det \left(\left[ \begin{array}{c c} I & 0 \\ - v ^ {*} & 1 \end{array} \right]\right) = \det \left(\left[ \begin{array}{c c} I & - \tau u \\ 0 & 1 - \tau v ^ {*} u \end{array} \right]\right). det ( [ I v ∗ 0 1 ] ) ⋅ det ( [ I − τu v ∗ 0 − τu 1 ] ) ⋅ det ( [ I − v ∗ 0 1 ] ) = det ( [ I 0 − τu 1 − τ v ∗ u ] ) .
所以
det ( E ( u , v , τ ) ) = det ( I − τ u v ∗ ) = 1 − τ v ∗ u . \det \left(E (u, v, \tau)\right) = \det (I - \tau u v ^ {*}) = 1 - \tau v ^ {*} u. det ( E ( u , v , τ ) ) = det ( I − τu v ∗ ) = 1 − τ v ∗ u . (2) 若 1 − τ v ∗ u ≠ 0 1 - \tau v^{*}u \neq 0 1 − τ v ∗ u = 0 det ( E ( u , v , τ ) ) ≠ 0 \operatorname{det}\left(E(u,v,\tau)\right) \neq 0 det ( E ( u , v , τ ) ) = 0 E ( u , v , τ ) E(u,v,\tau) E ( u , v , τ )
E ( u , v , τ ) E ( u , v , γ ) = I − τ u v ∗ − γ ( 1 − τ v ∗ u ) u v ∗ = I − τ u v ∗ − τ τ v ∗ u − 1 ( 1 − τ v ∗ u ) u v ∗ = I . \begin{array}{l} E (u, v, \tau) E (u, v, \gamma) = I - \tau u v ^ {*} - \gamma (1 - \tau v ^ {*} u) u v ^ {*} \\ = I - \tau u v ^ {*} - \frac {\tau}{\tau v ^ {*} u - 1} (1 - \tau v ^ {*} u) u v ^ {*} \\ = I. \\ \end{array} E ( u , v , τ ) E ( u , v , γ ) = I − τu v ∗ − γ ( 1 − τ v ∗ u ) u v ∗ = I − τu v ∗ − τ v ∗ u − 1 τ ( 1 − τ v ∗ u ) u v ∗ = I . (3) 留作练习.
更一般地, 我们有下面的结论
Sylverster 降幂公式 设 A ∈ C m × n , B ∈ C n × m A\in \mathbb{C}^{m\times n},B\in \mathbb{C}^{n\times m} A ∈ C m × n , B ∈ C n × m m ≥ n m\geq n m ≥ n
det ( λ I − A B ) = λ m − n det ( λ I − B A ) . (3.4) \det (\lambda I - A B) = \lambda^ {m - n} \det (\lambda I - B A). \tag {3.4} det ( λ I − A B ) = λ m − n det ( λ I − B A ) . ( 3.4 ) 因此 A B AB A B B A BA B A
(留作练习)
定理3.2 设 A ∈ C n × n A \in \mathbb{C}^{n \times n} A ∈ C n × n A A A A A A
3.2.2 Gauss变换 设 l j = [ 0 , … , 0 , l j + 1 , j , … , l n , j ] ⊤ , j = 1 , 2 , … , n , l_{j} = [0,\dots ,0,l_{j + 1,j},\dots ,l_{n,j}]^{\top},j = 1,2,\dots ,n, l j = [ 0 , … , 0 , l j + 1 , j , … , l n , j ] ⊤ , j = 1 , 2 , … , n ,
L ( l j ) ≜ E ( l j , e j , − 1 ) = I + l j e j T = [ 1 ⋱ 1 l j + 1 , j 1 ⋮ ⋱ l n , j 1 ] . L (l _ {j}) \triangleq E (l _ {j}, e _ {j}, - 1) = I + l _ {j} e _ {j} ^ {\mathsf {T}} = \left[ \begin{array}{c c c c c c} 1 & & & & & \\ & \ddots & & & & \\ & & 1 & & & \\ & & l _ {j + 1, j} & 1 & & \\ & & \vdots & & \ddots & \\ & & l _ {n, j} & & & 1 \end{array} \right]. L ( l j ) ≜ E ( l j , e j , − 1 ) = I + l j e j T = 1 ⋱ 1 l j + 1 , j ⋮ l n , j 1 ⋱ 1 . 显然, Gauss 变换也属于初等矩阵变换. 向量 l j l_{j} l j
det ( L ( l j ) ) = 1 , ( L ( l j ) ) − 1 = E ( l j , e j , 1 ) = E ( − l j , e j , − 1 ) = L ( − l j ) . \det (L (l _ {j})) = 1, \quad (L (l _ {j})) ^ {- 1} = E (l _ {j}, e _ {j}, 1) = E (- l _ {j}, e _ {j}, - 1) = L (- l _ {j}). det ( L ( l j )) = 1 , ( L ( l j ) ) − 1 = E ( l j , e j , 1 ) = E ( − l j , e j , − 1 ) = L ( − l j ) . Gauss变换是对单位矩阵的秩1修正, 主要功能是消零, 即将指定的某些元素变为零.
3.2.3 Householder变换 定义3.1 我们称矩阵
H = I − β v v ∗ , 0 ≠ v ∈ C n , β = 2 v ∗ v (3.5) H = I - \beta v v ^ {*}, \quad 0 \neq v \in \mathbb {C} ^ {n}, \quad \beta = \frac {2}{v ^ {*} v} \tag {3.5} H = I − β v v ∗ , 0 = v ∈ C n , β = v ∗ v 2 ( 3.5 ) 为 Householder 矩阵或 Householder 变换, 向量 v v v H ( v ) H(v) H ( v )
Householder 矩阵也是初等矩阵.
H = I − 2 v v ∗ , v ∈ C n 且 ∥ v ∥ 2 = 1. H = I - 2 v v ^ {*}, \quad v \in \mathbb {C} ^ {n} \text {且} \| v \| _ {2} = 1. H = I − 2 v v ∗ , v ∈ C n 且 ∥ v ∥ 2 = 1. Householder 矩阵有时也称为初等 Hermite 矩阵 [151].
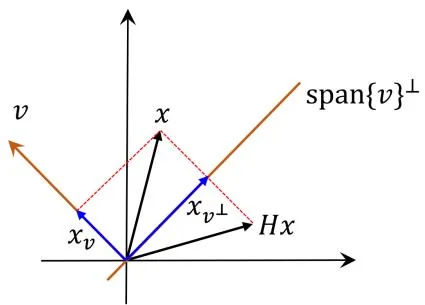
从几何上看, 一个 Householder 变换是一个关于超平面 span { v } ⊥ \operatorname{span}\{v\}^{\perp} span { v } ⊥ C n = span { v } ⊕ span { v } ⊥ \mathbb{C}^n = \operatorname{span}\{v\} \oplus \operatorname{span}\{v\}^{\perp} C n = span { v } ⊕ span { v } ⊥ x ∈ C n x \in \mathbb{C}^n x ∈ C n
x = x v + x v ⊥ , 其 中 x v ∈ span { v } , x v ⊥ ∈ span { v } ⊥ . x = x _ {v} + x _ {v ^ {\perp}}, \quad \text {其 中} \quad x _ {v} \in \operatorname {s p a n} \{v \}, x _ {v ^ {\perp}} \in \operatorname {s p a n} \{v \} ^ {\perp}. x = x v + x v ⊥ , 其 中 x v ∈ span { v } , x v ⊥ ∈ span { v } ⊥ . 易知 x v = v ∗ x v ∗ v v . x_{v} = \frac{v^{*}x}{v^{*}v} v. x v = v ∗ v v ∗ x v .
H x = x − β v v ∗ x = x − 2 v ∗ x v ∗ v v = − v ∗ x v ∗ v v + x v ⊥ = − x v + x v ⊥ , H x = x - \beta v v ^ {*} x = x - \frac {2 v ^ {*} x}{v ^ {*} v} v = - \frac {v ^ {*} x}{v ^ {*} v} v + x _ {v ^ {\perp}} = - x _ {v} + x _ {v ^ {\perp}}, H x = x − β v v ∗ x = x − v ∗ v 2 v ∗ x v = − v ∗ v v ∗ x v + x v ⊥ = − x v + x v ⊥ , 即 H x Hx H x x x x span { v } ⊥ \operatorname{span}\{v\}^{\perp} span { v } ⊥ v v v H x Hx H x x x x span { v } ⊥ \operatorname{span}\{v\}^{\perp} span { v } ⊥
下面是关于Householder矩阵的几个基本性质
定理3.3 设 H ∈ C n × n H \in \mathbb{C}^{n \times n} H ∈ C n × n
(1) H ∗ = H H^{*} = H H ∗ = H H H H H ∗ H = I H^{*}H = I H ∗ H = I H H H H 2 = I H^{2} = I H 2 = I H − 1 = H H^{-1} = H H − 1 = H det ( H ) = − 1 \operatorname{det}(H) = -1 det ( H ) = − 1 H H H λ = 1 \lambda = 1 λ = 1 λ = − 1 \lambda = -1 λ = − 1 λ = 1 \lambda = 1 λ = 1 n − 1 n - 1 n − 1
Householder 矩阵的一个非常重要的应用就是可以将一个向量除第一个元素以外的所有元素都化为零. 我们首先给出一个引理.
引理3.4设 x , y ∈ C n x,y\in \mathbb{C}^n x , y ∈ C n H ( v ) H(v) H ( v ) y = H ( v ) x y = H(v)x y = H ( v ) x ∥ x ∥ 2 = ∥ y ∥ 2 \| x\| _2 = \| y\| _2 ∥ x ∥ 2 = ∥ y ∥ 2 x ∗ y ∈ R x^{*}y\in \mathbb{R} x ∗ y ∈ R
证明. 若 ∥ x ∥ 2 = ∥ y ∥ 2 \| x\| _2 = \| y\| _2 ∥ x ∥ 2 = ∥ y ∥ 2 x ∗ y ∈ R x^{*}y\in \mathbb{R} x ∗ y ∈ R y ∗ y = x ∗ x y^{*}y = x^{*}x y ∗ y = x ∗ x x ∗ y = y ∗ x . x^{*}y = y^{*}x. x ∗ y = y ∗ x .
∥ x − y ∥ 2 2 = ( x − y ) ∗ ( x − y ) = x ∗ x − y ∗ x − x ∗ y + y ∗ y = 2 ( x ∗ x − y ∗ x ) . \left\| x - y \right\| _ {2} ^ {2} = (x - y) ^ {*} (x - y) = x ^ {*} x - y ^ {*} x - x ^ {*} y + y ^ {*} y = 2 \left(x ^ {*} x - y ^ {*} x\right). ∥ x − y ∥ 2 2 = ( x − y ) ∗ ( x − y ) = x ∗ x − y ∗ x − x ∗ y + y ∗ y = 2 ( x ∗ x − y ∗ x ) . 令 v = x − y v = x - y v = x − y
H ( v ) x = x − 2 ( x − y ) ( x − y ) ∗ x ∥ x − y ∥ 2 2 = x − 2 ( x − y ) ( x ∗ x − y ∗ x ) 2 ( x ∗ x − y ∗ x ) = y , H (v) x = x - \frac {2 (x - y) (x - y) ^ {*} x}{\| x - y \| _ {2} ^ {2}} = x - \frac {2 (x - y) (x ^ {*} x - y ^ {*} x)}{2 (x ^ {*} x - y ^ {*} x)} = y, H ( v ) x = x − ∥ x − y ∥ 2 2 2 ( x − y ) ( x − y ) ∗ x = x − 2 ( x ∗ x − y ∗ x ) 2 ( x − y ) ( x ∗ x − y ∗ x ) = y , 即存在 Householder 矩阵 H ( v ) H(v) H ( v ) y = H ( v ) x y = H(v)x y = H ( v ) x
反之, 如果存在 Householder 矩阵 H H H y = H x y = Hx y = H x H H H x ∗ y = x ∗ H x ∈ R x^{*}y = x^{*}Hx \in \mathbb{R} x ∗ y = x ∗ H x ∈ R H H H ∥ y ∥ 2 = ∥ H x ∥ 2 = ∥ x ∥ 2 \|y\|_{2} = \|Hx\|_{2} = \|x\|_{2} ∥ y ∥ 2 = ∥ H x ∥ 2 = ∥ x ∥ 2
Householder 向量也可以取 v = e i θ ( x − y ) , 0 ≤ θ < 2 π v = e^{\mathrm{i}\theta}(x - y), 0 \leq \theta < 2\pi v = e i θ ( x − y ) , 0 ≤ θ < 2 π
如果 x , y x, y x , y x ∗ y ∈ R x^{*}y \in \mathbb{R} x ∗ y ∈ R ∥ x ∥ 2 = ∥ y ∥ 2 \| x \|_{2} = \| y \|_{2} ∥ x ∥ 2 = ∥ y ∥ 2
由引理3.4, 我们可以立即得到下面的结论
定理3.5设 x = [ x 1 , x 2 , … , x n ] ⊤ ∈ R n x = [x_{1},x_{2},\ldots ,x_{n}]^{\top}\in \mathbb{R}^{n} x = [ x 1 , x 2 , … , x n ] ⊤ ∈ R n H ( v ) H(v) H ( v ) H ( v ) x = α e 1 H(v)x = \alpha e_1 H ( v ) x = α e 1 α = ∥ x ∥ 2 \alpha = \| x\| _2 α = ∥ x ∥ 2 α = − ∥ x ∥ 2 ) , e 1 = [ 1 , 0 , … , 0 ] ⊤ ∈ R n . \alpha = -\| x\| _2),e_1 = [1,0,\dots ,0]^{\top}\in \mathbb{R}^{n}. α = − ∥ x ∥ 2 ) , e 1 = [ 1 , 0 , … , 0 ] ⊤ ∈ R n .
在后面的讨论中, 我们将定理中的向量 v v v x x x
设 x = [ x 1 , x 2 , … , x n ] T ∈ R n x = [x_{1}, x_{2}, \ldots, x_{n}]^{\mathsf{T}} \in \mathbb{R}^{n} x = [ x 1 , x 2 , … , x n ] T ∈ R n H ( v ) H(v) H ( v ) v v v
v = x − α e 1 = [ x 1 − α , x 2 , … , x n ] ⊺ . v = x - \alpha e _ {1} = \left[ x _ {1} - \alpha , x _ {2}, \dots , x _ {n} \right] ^ {\intercal}. v = x − α e 1 = [ x 1 − α , x 2 , … , x n ] ⊺ . 在实际计算中, 为了尽可能地减少舍入误差, 我们通常避免两个相近的数做减运算, 否则就会损失有效数字. 因此, 我通常取
α = − sign ( x 1 ) ⋅ ∥ x ∥ 2 . (3.6) \alpha = - \operatorname {s i g n} \left(x _ {1}\right) \cdot \| x \| _ {2}. \tag {3.6} α = − sign ( x 1 ) ⋅ ∥ x ∥ 2 . ( 3.6 ) 事实上, 我们也可以取 α = s i g n ( x 1 ) ∥ x ∥ 2 \alpha = \mathrm{sign}(x_1)\| x\| _2 α = sign ( x 1 ) ∥ x ∥ 2 v v v v 1 v_{1} v 1
α = sign ( x 1 ) ∥ x ∥ 2 , v 1 = x 1 − α = x 1 2 − ∥ x ∥ 2 2 x 1 + α = − ( x 2 2 + x 3 2 + ⋯ + x n 2 ) x 1 + α . (3.7) \alpha = \operatorname {s i g n} \left(x _ {1}\right) \| x \| _ {2}, \quad v _ {1} = x _ {1} - \alpha = \frac {x _ {1} ^ {2} - \| x \| _ {2} ^ {2}}{x _ {1} + \alpha} = \frac {- \left(x _ {2} ^ {2} + x _ {3} ^ {2} + \cdots + x _ {n} ^ {2}\right)}{x _ {1} + \alpha}. \tag {3.7} α = sign ( x 1 ) ∥ x ∥ 2 , v 1 = x 1 − α = x 1 + α x 1 2 − ∥ x ∥ 2 2 = x 1 + α − ( x 2 2 + x 3 2 + ⋯ + x n 2 ) . ( 3.7 ) 在 v 1 v_{1} v 1 α \alpha α x 1 x_{1} x 1 α \alpha α
v 1 = { x 1 − α , i f s i g n ( x 1 ) < 0 − ( x 2 2 + x 3 2 + ⋯ + x n 2 ) x 1 + α , o t h e r w i s e v _ {1} = \left\{ \begin{array}{l l} x _ {1} - \alpha , & \text {i f s i g n} (x _ {1}) < 0 \\ \frac {- (x _ {2} ^ {2} + x _ {3} ^ {2} + \cdots + x _ {n} ^ {2})}{x _ {1} + \alpha}, & \text {o t h e r w i s e} \end{array} \right. v 1 = { x 1 − α , x 1 + α − ( x 2 2 + x 3 2 + ⋯ + x n 2 ) , i f s i g n ( x 1 ) < 0 o t h e r w i s e 无论怎样选取 α \alpha α H = I − β v v ∗ H = I - \beta vv^{*} H = I − β v v ∗
β = 2 v ∗ v = 2 ( x 1 − α ) 2 + x 2 2 + ⋯ + x n 2 = 2 2 α 2 − 2 α x 1 = − 1 α v 1 . \beta = \frac {2}{v ^ {*} v} = \frac {2}{(x _ {1} - \alpha) ^ {2} + x _ {2} ^ {2} + \cdots + x _ {n} ^ {2}} = \frac {2}{2 \alpha^ {2} - 2 \alpha x _ {1}} = - \frac {1}{\alpha v _ {1}}. β = v ∗ v 2 = ( x 1 − α ) 2 + x 2 2 + ⋯ + x n 2 2 = 2 α 2 − 2 α x 1 2 = − α v 1 1 .
思考:如果 x x x
在实数域中计算Householder向量 v v v 2 n 2n 2 n 3 n 3n 3 n
算法3.1.计算Householder向量 % \% % x ∈ R n x \in \mathbb{R}^n x ∈ R n v ∈ R n v \in \mathbb{R}^n v ∈ R n H x = ∥ x ∥ 2 e 1 Hx = \| x\|_2 e_1 H x = ∥ x ∥ 2 e 1 H = I − β v v ∗ H = I - \beta vv^* H = I − β v v ∗
1: function [ β , v ] = H o u s e ( x ) [\beta, v] = \mathbf{House}(x) [ β , v ] = House ( x ) n = length ( x ) n = \text{length}(x) n = length ( x ) length ( x ) \text{length}(x) length ( x ) x x x σ = x 2 2 + x 3 2 + ⋯ + x n 2 \sigma = x_2^2 +x_3^2 +\dots +x_n^2 σ = x 2 2 + x 3 2 + ⋯ + x n 2 v = x v = x v = x σ = 0 \sigma = 0 σ = 0 x 1 > = 0 x_{1} > = 0 x 1 >= 0 β = 0 \beta = 0 β = 0 % v 1 = 0 \% v_{1} = 0 % v 1 = 0 σ = 0 \sigma = 0 σ = 0 x 1 < 0 x_{1} < 0 x 1 < 0 v 1 = 2 x 1 , β = 2 / v 1 2 v_{1} = 2x_{1},\beta = 2 / v_{1}^{2} v 1 = 2 x 1 , β = 2/ v 1 2 α = x 1 2 + σ % α = ∥ x ∥ 2 \alpha = \sqrt{x_1^2 + \sigma} \quad \% \alpha = \| x\|_2 α = x 1 2 + σ % α = ∥ x ∥ 2 x 1 < = 0 x_{1} < = 0 x 1 <= 0 v 1 = x 1 − α v_{1} = x_{1} - \alpha v 1 = x 1 − α v 1 = − σ / ( x 1 + α ) v_{1} = -\sigma /(x_{1} + \alpha) v 1 = − σ / ( x 1 + α ) β = 2 / ( v 1 2 + σ ) \beta = 2 / (v_1^2 +\sigma) β = 2/ ( v 1 2 + σ )
可以证明,上述算法具有很好的数值稳定性[135],即
∥ H ~ − H ∥ 2 = O ( ε u ) , \| \tilde {H} - H \| _ {2} = \mathcal {O} (\varepsilon_ {u}), ∥ H ~ − H ∥ 2 = O ( ε u ) , 其中 H ~ \tilde{H} H ~ ε u \varepsilon_{u} ε u
在实际计算时, 我们可以将向量 v v v v 1 = 1 v_{1} = 1 v 1 = 1 v v v v ( 2 : n ) v(2:n) v ( 2 : n ) x ( 2 : n ) x(2:n) x ( 2 : n ) x x x
思考: 这里要求 v 1 ≠ 0 v_{1} \neq 0 v 1 = 0 v 1 = 0 v_{1} = 0 v 1 = 0
为了避免可能产生的溢出, 我们也可以事先将 x x x x = x / ∥ x ∥ 2 x = x / \| x\| _2 x = x /∥ x ∥ 2
Householder 变换与矩阵的乘积 设 A ∈ R m × n , H = I − β v v ∗ ∈ R m × m A\in \mathbb{R}^{m\times n},H = I - \beta vv^{*}\in \mathbb{R}^{m\times m} A ∈ R m × n , H = I − β v v ∗ ∈ R m × m
H A = ( I − β v v ∗ ) A = A − β v ( v ∗ A ) . H A = (I - \beta v v ^ {*}) A = A - \beta v (v ^ {*} A). H A = ( I − β v v ∗ ) A = A − β v ( v ∗ A ) . 因此, 在做 Householder 变换时, 并不需要生成 Householder 矩阵, 只需要 Householder 向量即可. 上面矩阵相乘的总运算量大约为 4 m n 4mn 4 mn
注记 Householder 矩阵早在 1932 年就出现了 [128], 但直到 1958 年才由 Householder 用于矩阵的三角化 [75].
关于其他类型的 Householder 变换 (包括复数情形), 可以参见 [36].
3.2.4 Givens变换 为简单起见, 我们这里这讨论实数域中的 Givens 变换. 设 θ ∈ [ 0 , 2 π ] \theta \in [0,2\pi] θ ∈ [ 0 , 2 π ]
G ( i , j , θ ) = [ 1 ⋱ c … s ⋮ ⋱ ⋮ − s … c ⋱ 1 ] ∈ R n × n , ( i ≤ j ) G (i, j, \theta) = \left[ \begin{array}{c c c c c c} 1 & & & & & \\ & \ddots & & & & \\ & & c & \dots & s & \\ & & \vdots & \ddots & \vdots & \\ & & - s & \dots & c & \\ & & & & \ddots & \\ & & & & & 1 \end{array} \right] \in \mathbb {R} ^ {n \times n}, \qquad (i \leq j) G ( i , j , θ ) = 1 ⋱ c ⋮ − s … ⋱ … s ⋮ c ⋱ 1 ∈ R n × n , ( i ≤ j ) 为Givens变换(或Givens旋转,或Givens矩阵),其中 c = cos ( θ ) c = \cos (\theta) c = cos ( θ ) s = sin ( θ ) s = \sin (\theta) s = sin ( θ ) ( i , i ) (i,i) ( i , i ) ( j , j ) (j,j) ( j , j ) c c c ( i , j ) (i,j) ( i , j ) ( j , i ) (j,i) ( j , i ) s s s − s -s − s G ( i , j , θ ) G(i,j,\theta) G ( i , j , θ )
定理3.6 G ( i , j , θ ) G(i,j,\theta) G ( i , j , θ ) det ( G ( i , j , θ ) ) = 1 \operatorname{det}(G(i,j,\theta)) = 1 det ( G ( i , j , θ )) = 1
Givens 变换不是初等矩阵变换, 事实上, 它是单位矩阵的一个秩 2 修正, 即
G ( i , j , θ ) = I + [ e i , e j ] [ c − 1 s − s c − 1 ] [ e i , e j ] T . G (i, j, \theta) = I + [ e _ {i}, e _ {j} ] \left[ \begin{array}{c c} c - 1 & s \\ - s & c - 1 \end{array} \right] [ e _ {i}, e _ {j} ] ^ {\mathsf {T}}. G ( i , j , θ ) = I + [ e i , e j ] [ c − 1 − s s c − 1 ] [ e i , e j ] T . 如果是定义在复数域上的Givens变换,则 c = e i α cos θ , s = e i β sin θ , 0 ≤ α , β , θ < 2 π . c = e^{\mathrm{i}\alpha}\cos \theta ,s = e^{\mathrm{i}\beta}\sin \theta ,0\leq \alpha ,\beta ,\theta < 2\pi . c = e i α cos θ , s = e i β sin θ , 0 ≤ α , β , θ < 2 π .
例3.1 设 x = [ x 1 x 2 ] ∈ R 2 x = \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} \in \mathbb{R}^2 x = [ x 1 x 2 ] ∈ R 2 G = [ c s − s c ] ∈ R 2 × 2 G = \begin{bmatrix} c & s \\ -s & c \end{bmatrix} \in \mathbb{R}^{2 \times 2} G = [ c − s s c ] ∈ R 2 × 2 G x = [ r 0 ] Gx = \begin{bmatrix} r \\ 0 \end{bmatrix} G x = [ r 0 ] c , s c, s c , s r r r
c = x 1 r , s = x 2 r , r = x 1 2 + x 2 2 , 即 G = 1 r [ x 1 x 2 − x 2 x 1 ] . c = {\frac {x _ {1}}{r}}, \quad s = {\frac {x _ {2}}{r}}, \quad r = {\sqrt {x _ {1} ^ {2} + x _ {2} ^ {2}}}, \quad \text {即} \quad G = {\frac {1}{r}} {\left[ \begin{array}{l l} {{x _ {1}}} & {{x _ {2}}} \\ {{- x _ {2}}} & {{x _ {1}}} \end{array} \right]}. c = r x 1 , s = r x 2 , r = x 1 2 + x 2 2 , 即 G = r 1 [ x 1 − x 2 x 2 x 1 ] . 也就是说, 通过Givens变换, 我们可以将向量 x ∈ R 2 x \in \mathbb{R}^2 x ∈ R 2
事实上, 对任意一个向量 x ∈ R n x \in \mathbb{R}^n x ∈ R n x x x
算法3.2.Givens变换 % \% % x = [ x 1 , x 2 ] T ∈ R 2 x = [x_1, x_2]^{\mathsf{T}} \in \mathbb{R}^2 x = [ x 1 , x 2 ] T ∈ R 2 c c c s s s G x = [ r , 0 ] T Gx = [r, 0]^{\mathsf{T}} G x = [ r , 0 ] T r = ∥ x ∥ 2 r = \|x\|_2 r = ∥ x ∥ 2 [ c , s ] = givens ( x 1 , x 2 ) [c, s] = \text{givens}(x_1, x_2) [ c , s ] = givens ( x 1 , x 2 ) x 2 = 0 x_{2} = 0 x 2 = 0 c = sign ( x 1 ) , s = 0 c = \operatorname{sign}(x_1),\quad s = 0 c = sign ( x 1 ) , s = 0 ∣ x 2 ∣ > ∣ x 1 ∣ |x_2| > |x_1| ∣ x 2 ∣ > ∣ x 1 ∣ τ = x 1 x 2 , s = s i g n ( x 2 ) 1 + τ 2 , c = s τ \tau = \frac{x_1}{x_2},\quad s = \frac{\mathrm{sign}(x_2)}{\sqrt{1 + \tau^2}},\quad c = s\tau τ = x 2 x 1 , s = 1 + τ 2 sign ( x 2 ) , c = s τ τ = x 2 x 1 , c = sign ( x 1 ) 1 + τ 2 , s = c τ \tau = \frac{x_2}{x_1},\quad c = \frac{\operatorname{sign}(x_1)}{\sqrt{1 + \tau^2}},\quad s = c\tau τ = x 1 x 2 , c = 1 + τ 2 sign ( x 1 ) , s = c τ
10: end if
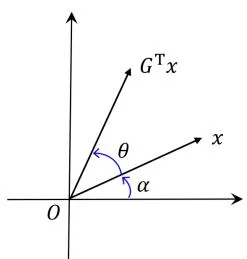
例3.2 (Givens变换的几何意义) 设 x = [ x 1 x 2 ] = [ r cos α r sin α ] ∈ R 2 x = \left[ \begin{array}{l} x_{1} \\ x_{2} \end{array} \right] = \left[ \begin{array}{l} r \cos \alpha \\ r \sin \alpha \end{array} \right] \in \mathbb{R}^{2} x = [ x 1 x 2 ] = [ r cos α r sin α ] ∈ R 2 r = x 1 2 + x 2 2 , α = arctan x 2 x 1 r = \sqrt{x_1^2 + x_2^2}, \alpha = \arctan \frac{x_2}{x_1} r = x 1 2 + x 2 2 , α = arctan x 1 x 2
G T x = [ cos θ sin θ − sin θ cos θ ] T [ r cos α r sin α ] = [ r ( cos θ cos α − sin θ sin α ) r ( sin θ cos α + cos θ sin α ) ] = [ r cos ( α + θ ) r sin ( α + θ ) ] , G ^ {\mathsf {T}} x = \left[ \begin{array}{c c} \cos \theta & \sin \theta \\ - \sin \theta & \cos \theta \end{array} \right] ^ {\mathsf {T}} \left[ \begin{array}{c} r \cos \alpha \\ r \sin \alpha \end{array} \right] = \left[ \begin{array}{c} r (\cos \theta \cos \alpha - \sin \theta \sin \alpha) \\ r (\sin \theta \cos \alpha + \cos \theta \sin \alpha) \end{array} \right] = \left[ \begin{array}{c} r \cos (\alpha + \theta) \\ r \sin (\alpha + \theta) \end{array} \right], G T x = [ cos θ − sin θ sin θ cos θ ] T [ r cos α r sin α ] = [ r ( cos θ cos α − sin θ sin α ) r ( sin θ cos α + cos θ sin α ) ] = [ r cos ( α + θ ) r sin ( α + θ ) ] , 也就是说, G T x G^{\mathsf{T}}x G T x x x x θ \theta θ θ = − α \theta = -\alpha θ = − α G x = [ r 0 ] Gx = \begin{bmatrix} r \\ 0 \end{bmatrix} G x = [ r 0 ]
Givens变换与矩阵的乘积 设 A ∈ R m × n A \in \mathbb{R}^{m \times n} A ∈ R m × n G = G ( i , j , θ ) ∈ R m G = G(i, j, \theta) \in \mathbb{R}^m G = G ( i , j , θ ) ∈ R m G ⊤ A G^\top A G ⊤ A i i i j j j A A A i i i j j j 6 n 6n 6 n
同样地, 如果是右乘Givens变换, 则只会影响其第 i i i j j j 6 m 6m 6 m
任何一个正交矩阵都可以写成若干个Householder矩阵或Givens矩阵的乘积(见习题3.5和3.23),所以正交矩阵所对应的线性变换可以看作是反射变换和旋转变换的推广,因此它不会改变向量的长度与(不同向量之间的)角度。
3.2.5 正交变换的舍入误差分析 引理3.7设 P ∈ R n × n P\in \mathbb{R}^{n\times n} P ∈ R n × n P ~ \tilde{P} P ~
fl ( P ~ A ) = P ( A + E ) , fl ( A P ~ ) = ( A + F ) P , \operatorname {f l} (\tilde {P} A) = P (A + E), \quad \operatorname {f l} (A \tilde {P}) = (A + F) P, fl ( P ~ A ) = P ( A + E ) , fl ( A P ~ ) = ( A + F ) P , 其中 ∥ E ∥ 2 = O ( ε u ) ⋅ ∥ A ∥ 2 , ∥ F ∥ 2 = O ( ε u ) ⋅ ∥ A ∥ 2 . \| E\| _2 = \mathcal{O}(\varepsilon_u)\cdot \| A\| _2,\| F\| _2 = \mathcal{O}(\varepsilon_u)\cdot \| A\| _2. ∥ E ∥ 2 = O ( ε u ) ⋅ ∥ A ∥ 2 , ∥ F ∥ 2 = O ( ε u ) ⋅ ∥ A ∥ 2 .
这说明对一个矩阵做Householder变换或Givens变换是向后稳定的.
定理3.8 考虑对矩阵 A A A
f l ( P ~ k … P ~ 1 A Q ~ 1 … Q ~ k ) = P k … P 1 ( A + E ) Q 1 … Q k , \mathrm {f l} \left(\tilde {P} _ {k} \dots \tilde {P} _ {1} A \tilde {Q} _ {1} \dots \tilde {Q} _ {k}\right) = P _ {k} \dots P _ {1} (A + E) Q _ {1} \dots Q _ {k}, fl ( P ~ k … P ~ 1 A Q ~ 1 … Q ~ k ) = P k … P 1 ( A + E ) Q 1 … Q k , 其中 ∥ E ∥ 2 = O ( ε u ) ⋅ ( k ∥ A ∥ 2 ) \| E\| _2 = \mathcal{O}(\varepsilon_u)\cdot (k\| A\| _2) ∥ E ∥ 2 = O ( ε u ) ⋅ ( k ∥ A ∥ 2 )
一般地, 假设 X X X X ~ \tilde{X} X ~ X X X A A A
fl ( X ~ A ) = X A + E = X ( A + X − 1 E ) ≜ X ( A + F ) , \operatorname {f l} (\tilde {X} A) = X A + E = X (A + X ^ {- 1} E) \triangleq X (A + F), fl ( X ~ A ) = X A + E = X ( A + X − 1 E ) ≜ X ( A + F ) , 其中 ∥ E ∥ 2 = O ( ε u ) ∥ X A ∥ 2 ≤ O ( ε u ) ∥ X ∥ 2 ∥ A ∥ 2 \| E\| _2 = \mathcal{O}(\varepsilon_u)\| X A\| _2\leq \mathcal{O}(\varepsilon_u)\| X\| _2\| A\| _2 ∥ E ∥ 2 = O ( ε u ) ∥ X A ∥ 2 ≤ O ( ε u ) ∥ X ∥ 2 ∥ A ∥ 2
∥ F ∥ 2 = ∥ X − 1 E ∥ 2 ≤ O ( ε u ) ∥ X − 1 ∥ 2 ∥ X ∥ 2 ∥ A ∥ 2 = O ( ε u ) κ 2 ( X ) ∥ A ∥ 2 . \| F \| _ {2} = \| X ^ {- 1} E \| _ {2} \leq \mathcal {O} (\varepsilon_ {u}) \| X ^ {- 1} \| _ {2} \| X \| _ {2} \| A \| _ {2} = \mathcal {O} (\varepsilon_ {u}) \kappa_ {2} (X) \| A \| _ {2}. ∥ F ∥ 2 = ∥ X − 1 E ∥ 2 ≤ O ( ε u ) ∥ X − 1 ∥ 2 ∥ X ∥ 2 ∥ A ∥ 2 = O ( ε u ) κ 2 ( X ) ∥ A ∥ 2 . 因此, 舍入误差可能会放大 κ 2 ( X ) \kappa_{2}(X) κ 2 ( X ) X X X κ 2 ( X ) \kappa_{2}(X) κ 2 ( X )