3.5 线性最小二乘问题的求解方法
3.5.1 正规方程
这里我们考虑超定线性最小二乘问题的求解
定理3.23 设 A∈Rm×n ( m≥n ). 则 x∗∈Rn 是线性最小二乘问题 (3.1) 的解当且仅当残量 r=b−Ax∗ 与 Ran(A) (值域) 正交, 即 x∗ 是下面的正规方程的解
AT(b−Ax)=0或ATAx=ATb.(3.22) (板书)
证明. 充分性: 设 x∗ 是正规方程 (3.21) 的解. 对任意向量 y∈Rn , 由 (b−Ax∗)⊥Ran(A) 可知
∥Ay−b∥22=∥(Ax∗−b)+A(y−x∗)∥22=∥Ax∗−b∥22+∥A(y−x∗)∥22≥∥Ax∗−b∥22. 因此, x∗ 是线性最小二乘问题 (3.1) 的解
必要性:设 x∗ 是线性最小二乘问题(3.1)的解.用反证法,假定 z≜AT(b−Ax∗)=0 取 y=x∗+αz ,其中 α>0 ,则有
∥Ay−b∥22=∥Ax∗−b+αAz∥22=∥Ax∗−b∥22−2α∥z∥22+α2∥Az∥22. 由于 ∥z∥2>0 ,当 α 充分小时,有 2∥z∥22>α∥Az∥22 ,即上式右端小于 ∥Ax∗−b∥22 .这与 x∗ 是最小二乘解相矛盾.所以 z=0 ,即 AT(b−Ax∗)=0.
由定理3.23可知, 求线性最小二乘问题(3.1)的解等价于求正规方程(3.21)的解. 由于
ATb∈Ran(AT)=Ran(ATA), 因此正规方程 ATAx=ATb 是相容 (consistent) 的, 即最小二乘解总是存在的. 当 A 非奇异时, 这个解也是唯一的.
定理3.24 设 A∈Rm×n ( m>n ). 则 ATA 对称正定当且仅当 A 是列满秩的, 即 rank(A)=n . 此时, 线性最小二乘问题 (3.1) 的解是唯一的, 其表达式为
x=(ATA)−1ATb. 最小二乘解的几何含义
根据定理3.23,我们可以把 b 写成
b=Ax∗+r,其 中r⊥Ran(A).(3.23) 所以 Ax∗ 就是 b 在 Ran(A) 上的正交投影,见图3.2
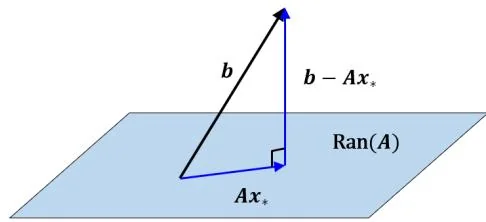
图3.2.最小二乘解的几何描述
最小二乘解可能并不唯一,但分解(3.22)总是唯一的
3.5.2 Cholesky分解法
当 A 列满秩时, 我们就可以使用 Cholesky 分解来求解正规方程, 总的运算量大约为 mn2+31n3+mn+O(n2) , 其中大部分的运算量 (mn2) 是用来计算 A⊤A (由于 A⊤A 对称, 因此只需计算其下三角部分).
通过直接求解正规方程来求解最小二乘问题, 运算量小, 而且简单直观.
但由于 ATA 的条件数是 A 的条件数的平方, 因此对于病态情形 (即 A 的条件数比较大), 不建议使用该方法.
例3.6 下面的例子说明, 计算 ATA 可能会损失计算精度: 设
A=1ε1ε1ε, 则
ATA=1+ε21111+ε21111+ε2. 记 εu 为机器精度, 则当 εu<ε<εu 时有 ε2<εu , 由于舍入误差的原因, 通过浮点运算计算得到的 ATA 是奇异的. 但我们注意到 A 是满秩的.
3.5.3 QR分解法
这里假定 A∈Rm×n ( m≥n ) 是满秩的. 设 A 的 QR 分解为 A=QR , 我们用三种不同的方法来推导线性最小二乘问题的解.
(1) 将 Q 的扩充成一个正交矩阵, 记为 [Q,Q^]∈Rm×m . 于是有
∥Ax−b∥22=[Q,Q^]T(Ax−b)22=[Q,Q^]T(QRx−b)22 =[Rx−QTb−Q^Tb]22=Rx−QTb22+Q^Tb22≥Q^Tb22, 等号成立当且仅当 Rx=QTb . 所以最小二乘解为
x∗=R−1Q⊺b. (2) 由于 Q 的列向量构成 Ran(A) 的一组单位正交基, 所以 QQT 和 I−QQT 分别是 Ran(A) 和 Ran(A)⊥ 上的正交投影矩阵. 又 Ax∈Ran(A) , 所以
∥Ax−b∥22=QQT(Ax−b)22+(I−QQT)(Ax−b)22=∥QRx−QQ⊤b∥22+∥(I−QQ⊤)b∥22=∥Rx−QTb∥22+∥(I−QQT)b∥22≥∥(I−QQT)b∥22, 等号成立当且仅当 Rx=QTb . 所以最小二乘解为
x∗=R−1QTb. 事实上,由图3.2可知, x∗ 满足
Ax∗=QQ⊺b, 即 QRx∗=QQTb, 由此可得 x∗=R−1QTb.
(3) 解正规方程. 由定理 3.23 可知, 最小二乘解为
x∗=(ATA)−1ATb=(RTQTQR)−1RTQTb=(RTR)−1RTQTb=R−1QTb. 用基于MGS的QR分解求解最小二乘问题时的运算量大约为 2mn2 ,而基于Householder变换的QR分解则只需 2mn2−2n3/3 (不需要显式计算 Q ,只需将Householder变换直接作用到 b 上即可计算出 QTb )。因此当 m≫n 时,QR分解法的计算量大约是Cholesky分解的两倍。
因此当 m≫n 时, QR 分解法的计算量大约是 Cholesky 分解法的两倍. 当 m=n 时, 几乎相同.
通常 QR 算法比较稳定, 是求解最小二乘问题的首选方法, 特别是当 A 条件数较大 (病态)时.
3.5.4 奇异值分解法
设 A∈Rm×n 列满秩, A=UnΣV⊤ 是 A 的降阶奇异值分解, 则
x∗=(ATA)−1ATb=(VΣUnTUnΣVT)−1VΣUnTb=(VΣ−2VT)VΣUnTb=VΣ−1UnTb. 相比于Cholesky分解法和QR分解,用SVD求解最小二乘问题具有更高的健壮性,但由于需要计算系数矩阵的SVD,运算量远超Cholesky分解法和QR分解.所以只有当系数矩阵秩亏或者接近秩亏时才使用(此时QR分解法可能会失效).
例3.7 分别用三种方法求解最小二乘问题, 比较运算时间.
(LS_3methods.m)
三种方法的运算时间如下 (A∈R2n×n,b∈Rn ,以秒为单位):
这里的计算时间可能受计算机系统和 MATLAB 矩阵运算优化影响, 并不一定能准确反映各种方法的实际运算量.
