6.3 应用: Poisson 方程求解 Poisson方程是一类典型的偏微分方程,经过差分离散后,转化为一个线性方程组.我们以这个线性方程组为例,讨论Jacobi,G-S和SOR迭代法的相关性质.
6.3.1 一维 Poisson 方程 首先介绍一维 Poisson 方程的离散. 考虑如下带 Dirichlet 边界条件的一维 Poisson 方程
{ − d 2 u ( x ) d x 2 = f ( x ) , 0 < x < 1 , u ( 0 ) = a , u ( 1 ) = b , (6.16) \left\{ \begin{array}{l} - \frac {\mathrm {d} ^ {2} u (x)}{\mathrm {d} x ^ {2}} = f (x), \quad 0 < x < 1, \\ u (0) = a, u (1) = b, \end{array} \right. \tag {6.16} { − d x 2 d 2 u ( x ) = f ( x ) , 0 < x < 1 , u ( 0 ) = a , u ( 1 ) = b , ( 6.16 ) 其中 f ( x ) f(x) f ( x ) u ( x ) u(x) u ( x )
差分离散 取步长 h = 1 n + 1 h = \frac{1}{n + 1} h = n + 1 1 x i = i h , i = 0 , 1 , 2 , … , n + 1. x_{i} = ih,i = 0,1,2,\ldots ,n + 1. x i = ih , i = 0 , 1 , 2 , … , n + 1.
− d 2 u ( x ) d x 2 ∣ x i = 2 u ( x i ) − u ( x i − 1 ) − u ( x i + 1 ) h 2 + O ( h 2 ∥ d 4 u d x 4 ∥ ∞ ) , i = 1 , 2 , … , n . - \frac {\mathrm {d} ^ {2} u (x)}{\mathrm {d} x ^ {2}} \Bigg | _ {x _ {i}} = \frac {2 u (x _ {i}) - u (x _ {i - 1}) - u (x _ {i + 1})}{h ^ {2}} + O \left(h ^ {2} \left\| \frac {\mathrm {d} ^ {4} u}{\mathrm {d} x ^ {4}} \right\| _ {\infty}\right), i = 1, 2, \ldots , n. − d x 2 d 2 u ( x ) x i = h 2 2 u ( x i ) − u ( x i − 1 ) − u ( x i + 1 ) + O ( h 2 d x 4 d 4 u ∞ ) , i = 1 , 2 , … , n . 将其代入 (6.9), 舍去高阶项后得到 Poisson 方程在 x i x_{i} x i
− u i − 1 + 2 u i − u i + 1 = h 2 f i , - u _ {i - 1} + 2 u _ {i} - u _ {i + 1} = h ^ {2} f _ {i}, − u i − 1 + 2 u i − u i + 1 = h 2 f i , 其中 f i = f ( x i ) , u i f_{i} = f(x_{i}),u_{i} f i = f ( x i ) , u i u ( x i ) u(x_{i}) u ( x i ) i = 1 , 2 , … , n , i = 1,2,\ldots ,n, i = 1 , 2 , … , n , n n n
T n u = f , (6.17) T _ {n} u = f, \tag {6.17} T n u = f , ( 6.17 ) 其中
T n = [ 2 − 1 − 1 ⋱ ⋱ ⋱ ⋱ − 1 − 1 2 ] ≜ tridiag ( − 1 , 2 , − 1 ) , u = [ u 1 u 2 ⋮ u n − 1 u n ] , f = [ f 1 + u 0 f 2 ⋮ f n − 1 f n + u n + 1 ] . (6.18) T _ {n} = \left[ \begin{array}{c c c c} 2 & - 1 & & \\ - 1 & \ddots & \ddots & \\ & \ddots & \ddots & - 1 \\ & & - 1 & 2 \end{array} \right] \triangleq \operatorname {t r i d i a g} (- 1, 2, - 1), \quad u = \left[ \begin{array}{c} u _ {1} \\ u _ {2} \\ \vdots \\ u _ {n - 1} \\ u _ {n} \end{array} \right], \quad f = \left[ \begin{array}{c} f _ {1} + u _ {0} \\ f _ {2} \\ \vdots \\ f _ {n - 1} \\ f _ {n} + u _ {n + 1} \end{array} \right]. \tag {6.18} T n = 2 − 1 − 1 ⋱ ⋱ ⋱ ⋱ − 1 − 1 2 ≜ tridiag ( − 1 , 2 , − 1 ) , u = u 1 u 2 ⋮ u n − 1 u n , f = f 1 + u 0 f 2 ⋮ f n − 1 f n + u n + 1 . ( 6.18 ) 由边界条件可知 u 0 = a , u n + 1 = b u_0 = a, u_{n+1} = b u 0 = a , u n + 1 = b
系数矩阵 T n T_{n} T n 易知 T n T_{n} T n
引理6.24 T n T_{n} T n
λ k = 2 − 2 cos k π n + 1 , \lambda_ {k} = 2 - 2 \cos \frac {k \pi}{n + 1}, λ k = 2 − 2 cos n + 1 kπ , z k = 2 n + 1 [ sin k π n + 1 , sin 2 k π n + 1 , … , sin n k π n + 1 ] T , k = 1 , 2 , … , n , z _ {k} = \sqrt {\frac {2}{n + 1}} \left[ \sin \frac {k \pi}{n + 1}, \sin \frac {2 k \pi}{n + 1}, \dots , \sin \frac {n k \pi}{n + 1} \right] ^ {\mathsf {T}}, \quad k = 1, 2, \dots , n, z k = n + 1 2 [ sin n + 1 kπ , sin n + 1 2 kπ , … , sin n + 1 nkπ ] T , k = 1 , 2 , … , n , 即 T n = Z Λ Z ⊤ T_{n} = Z\Lambda Z^{\top} T n = Z Λ Z ⊤ Λ = d i a g ( λ 1 , λ 2 , … , λ n ) \Lambda = \mathrm{diag}(\lambda_1,\lambda_2,\ldots ,\lambda_n) Λ = diag ( λ 1 , λ 2 , … , λ n ) Z = [ z 1 , z 2 , … , z n ] Z = [z_{1},z_{2},\dots ,z_{n}] Z = [ z 1 , z 2 , … , z n ]
(留作课外自习, 直接代入验证即可)
由此可知, T n T_{n} T n
推论6.25 设 T = t r i d i a g ( a , b , c ) ∈ R n × n , a c > 0 T = \mathrm{tridiag}(a,b,c) \in \mathbb{R}^{n \times n}, ac > 0 T = tridiag ( a , b , c ) ∈ R n × n , a c > 0 T T T
λ k = b − 2 a c cos k π n + 1 , k = 1 , 2 , … , n , \lambda_ {k} = b - 2 \sqrt {a c} \cos \frac {k \pi}{n + 1}, \quad k = 1, 2, \ldots , n, λ k = b − 2 a c cos n + 1 kπ , k = 1 , 2 , … , n , 对应的特征向量为 z k z_{k} z k j j j
z k ( j ) = ( a c ) j 2 sin j k π n + 1 . z _ {k} (j) = \left(\frac {a}{c}\right) ^ {\frac {j}{2}} \sin \frac {j k \pi}{n + 1}. z k ( j ) = ( c a ) 2 j sin n + 1 jkπ . 特别地, 若 a = c = 1 a = c = 1 a = c = 1
z k = 2 n + 1 [ sin k π n + 1 , sin 2 k π n + 1 , … , sin n k π n + 1 ] T . z _ {k} = \sqrt {\frac {2}{n + 1}} \left[ \sin \frac {k \pi}{n + 1}, \sin \frac {2 k \pi}{n + 1}, \ldots , \sin \frac {n k \pi}{n + 1} \right] ^ {\mathsf {T}}. z k = n + 1 2 [ sin n + 1 kπ , sin n + 1 2 kπ , … , sin n + 1 nkπ ] T . (留作练习)
由引理6.24可知, T n T_{n} T n
2 ( 1 − cos n π n + 1 ) = 4 sin 2 n π 2 ( n + 1 ) ≈ 4 , 2 \left(1 - \cos \frac {n \pi}{n + 1}\right) = 4 \sin^ {2} \frac {n \pi}{2 (n + 1)} \approx 4, 2 ( 1 − cos n + 1 nπ ) = 4 sin 2 2 ( n + 1 ) nπ ≈ 4 , 最小特征值为
2 ( 1 − cos π n + 1 ) = 4 sin 2 π 2 ( n + 1 ) ≈ ( π n + 1 ) 2 . 2 \left(1 - \cos \frac {\pi}{n + 1}\right) = 4 \sin^ {2} \frac {\pi}{2 (n + 1)} \approx \left(\frac {\pi}{n + 1}\right) ^ {2}. 2 ( 1 − cos n + 1 π ) = 4 sin 2 2 ( n + 1 ) π ≈ ( n + 1 π ) 2 . 因此, 当 n n n T n T_{n} T n
κ 2 ( T n ) ≈ 4 ( n + 1 ) 2 π 2 . \kappa_ {2} (T _ {n}) \approx \frac {4 (n + 1) ^ {2}}{\pi^ {2}}. κ 2 ( T n ) ≈ π 2 4 ( n + 1 ) 2 . 6.3.2 二维Poisson方程 考虑二维 Poisson 方程的离散. 同样是带 Dirichlet 边界条件, 即
{ − Δ u ( x , y ) = − ∂ 2 u ( x , y ) ∂ x 2 − ∂ 2 u ( x , y ) ∂ y 2 = f ( x , y ) , ( x , y ) ∈ Ω , u ( x , y ) = u 0 ( x , y ) , ( x , y ) ∈ ∂ Ω , (6.19) \left\{ \begin{array}{l} - \Delta u (x, y) = - \frac {\partial^ {2} u (x , y)}{\partial x ^ {2}} - \frac {\partial^ {2} u (x , y)}{\partial y ^ {2}} = f (x, y), \quad (x, y) \in \Omega , \\ u (x, y) = u _ {0} (x, y), \quad (x, y) \in \partial \Omega , \end{array} \right. \tag {6.19} { − Δ u ( x , y ) = − ∂ x 2 ∂ 2 u ( x , y ) − ∂ y 2 ∂ 2 u ( x , y ) = f ( x , y ) , ( x , y ) ∈ Ω , u ( x , y ) = u 0 ( x , y ) , ( x , y ) ∈ ∂ Ω , ( 6.19 ) 其中 Ω = [ 0 , 1 ] × [ 0 , 1 ] \Omega = [0,1]\times [0,1] Ω = [ 0 , 1 ] × [ 0 , 1 ] ∂ Ω \partial \Omega ∂ Ω Ω \Omega Ω
五点差分离散 为了简单起见, 我们在 x x x y y y h = 1 n + 1 h = \frac{1}{n + 1} h = n + 1 1 x i = i h x_{i} = ih x i = ih y j = j h y_{j} = jh y j = jh i , j = 0 , 1 , 2 , … , n + 1 i, j = 0, 1, 2, \ldots, n + 1 i , j = 0 , 1 , 2 , … , n + 1 x x x y y y
− ∂ 2 u ( x , y ) ∂ x 2 ∣ ( x i , y j ) ≈ 2 u ( x i , y j ) − u ( x i − 1 , y j ) − u ( x i + 1 , y j ) h 2 , − ∂ 2 u ( x , y ) ∂ y 2 ∣ ( x i , y j ) ≈ 2 u ( x i , y j ) − u ( x i , y j − 1 ) − u ( x i , y j + 1 ) h 2 . \begin{array}{l} \left. - \frac {\partial^ {2} u (x , y)}{\partial x ^ {2}} \right| _ {(x _ {i}, y _ {j})} \approx \frac {2 u (x _ {i} , y _ {j}) - u (x _ {i - 1} , y _ {j}) - u (x _ {i + 1} , y _ {j})}{h ^ {2}}, \\ - \frac {\partial^ {2} u (x , y)}{\partial y ^ {2}} \bigg | _ {(x _ {i}, y _ {j})} \approx \frac {2 u (x _ {i} , y _ {j}) - u (x _ {i} , y _ {j - 1}) - u (x _ {i} , y _ {j + 1})}{h ^ {2}}. \\ \end{array} − ∂ x 2 ∂ 2 u ( x , y ) ( x i , y j ) ≈ h 2 2 u ( x i , y j ) − u ( x i − 1 , y j ) − u ( x i + 1 , y j ) , − ∂ y 2 ∂ 2 u ( x , y ) ( x i , y j ) ≈ h 2 2 u ( x i , y j ) − u ( x i , y j − 1 ) − u ( x i , y j + 1 ) . 代入 (6.12) 后, 就可以得到二维 Poisson 方程在 ( x i , y j ) (x_{i}, y_{j}) ( x i , y j )
4 u i , j − u i − 1 , j − u i + 1 , j − u i , j − 1 − u i , j + 1 = h 2 f i , j , 4 u _ {i, j} - u _ {i - 1, j} - u _ {i + 1, j} - u _ {i, j - 1} - u _ {i, j + 1} = h ^ {2} f _ {i, j}, 4 u i , j − u i − 1 , j − u i + 1 , j − u i , j − 1 − u i , j + 1 = h 2 f i , j , 其中 f i , j = f ( x i , y j ) , u i , j f_{i,j} = f(x_i,y_j),u_{i,j} f i , j = f ( x i , y j ) , u i , j u ( x i , y j ) u(x_{i},y_{j}) u ( x i , y j )
按自然顺序排列以上方程 (即先沿 x x x y y y
T N u = h 2 f , (6.20) T _ {N} u = h ^ {2} f, \tag {6.20} T N u = h 2 f , ( 6.20 ) 其中
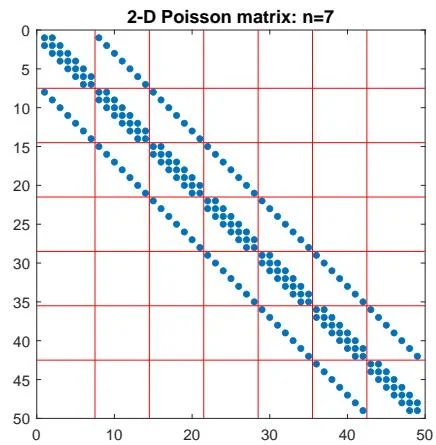
T N ≜ I ⊗ T n + T n ⊗ I , u = [ u 1 , 1 , … , u n , 1 , u 1 , 2 , … , u n , 2 , … , u 1 , n , … , u n , n ] ⊤ . T _ {N} \triangleq I \otimes T _ {n} + T _ {n} \otimes I, \quad u = \left[ u _ {1, 1}, \dots , u _ {n, 1}, u _ {1, 2}, \dots , u _ {n, 2}, \dots , u _ {1, n}, \dots , u _ {n, n} \right] ^ {\top}. T N ≜ I ⊗ T n + T n ⊗ I , u = [ u 1 , 1 , … , u n , 1 , u 1 , 2 , … , u n , 2 , … , u 1 , n , … , u n , n ] ⊤ . 这里 ⊗ \otimes ⊗ T n T_{n} T n N = 7 2 N = 7^{2} N = 7 2
需要注意的是, 系数矩阵 T N T_{N} T N T N T_{N} T N
T n ⊗ I ⊗ I + I ⊗ T n ⊗ I + I ⊗ I ⊗ T n . T _ {n} \otimes I \otimes I + I \otimes T _ {n} \otimes I + I \otimes I \otimes T _ {n}. T n ⊗ I ⊗ I + I ⊗ T n ⊗ I + I ⊗ I ⊗ T n . 系数矩阵 T N T_{N} T N 定理6.26 设 T n = Z Λ Z ⊤ T_{n} = Z\Lambda Z^{\top} T n = Z Λ Z ⊤ Z = [ z 1 , z 2 , … , z n ] Z = [z_{1}, z_{2}, \ldots, z_{n}] Z = [ z 1 , z 2 , … , z n ] Λ = d i a g ( λ 1 , λ 2 , … , λ n ) \Lambda = \mathrm{diag}(\lambda_{1}, \lambda_{2}, \ldots, \lambda_{n}) Λ = diag ( λ 1 , λ 2 , … , λ n ) T N T_{N} T N
T N = ( Z ⊗ Z ) ( I ⊗ Λ + Λ ⊗ I ) ( Z ⊗ Z ) T , T _ {N} = (Z \otimes Z) (I \otimes \Lambda + \Lambda \otimes I) (Z \otimes Z) ^ {\mathsf {T}}, T N = ( Z ⊗ Z ) ( I ⊗ Λ + Λ ⊗ I ) ( Z ⊗ Z ) T , 即 T N T_{N} T N λ i + λ j \lambda_{i} + \lambda_{j} λ i + λ j z i ⊗ z j , i , j = 1 , 2 , … , n z_{i} \otimes z_{j}, i, j = 1,2,\ldots,n z i ⊗ z j , i , j = 1 , 2 , … , n
由于 T N T_{N} T N
κ ( T N ) = λ max ( T N ) λ min ( T N ) = 1 − cos n π n + 1 1 − cos π n + 1 = sin 2 n π 2 ( n + 1 ) sin 2 π 2 ( n + 1 ) ≈ 4 ( n + 1 ) 2 π 2 . \kappa (T _ {N}) = \frac {\lambda_ {\max} (T _ {N})}{\lambda_ {\min} (T _ {N})} = \frac {1 - \cos \frac {n \pi}{n + 1}}{1 - \cos \frac {\pi}{n + 1}} = \frac {\sin^ {2} \frac {n \pi}{2 (n + 1)}}{\sin^ {2} \frac {\pi}{2 (n + 1)}} \approx \frac {4 (n + 1) ^ {2}}{\pi^ {2}}. κ ( T N ) = λ m i n ( T N ) λ m a x ( T N ) = 1 − cos n + 1 π 1 − cos n + 1 nπ = sin 2 2 ( n + 1 ) π sin 2 2 ( n + 1 ) nπ ≈ π 2 4 ( n + 1 ) 2 . 故当 n n n κ ( T N ) \kappa(T_N) κ ( T N ) T N T_N T N
求解二维离散 Poisson 方程的 Jacobi 迭代法
算法6.5. 求解二维离散Poisson方程的Jacobi迭代法u ( 0 ) ∈ R N u^{(0)} \in \mathbb{R}^N u ( 0 ) ∈ R N i = 1 i = 1 i = 1 n n n j = 1 j = 1 j = 1 n n n u i , j ( k + 1 ) = 1 4 ( h 2 f i , j + u i + 1 , j ( k ) + u i − 1 , j ( k ) + u i , j + 1 ( k ) + u i , j − 1 ( k ) ) u_{i,j}^{(k + 1)} = \frac{1}{4}\left(h^2 f_{i,j} + u_{i + 1,j}^{(k)} + u_{i - 1,j}^{(k)} + u_{i,j + 1}^{(k)} + u_{i,j - 1}^{(k)}\right) u i , j ( k + 1 ) = 4 1 ( h 2 f i , j + u i + 1 , j ( k ) + u i − 1 , j ( k ) + u i , j + 1 ( k ) + u i , j − 1 ( k ) )
求解二维离散 Poisson 方程的 G-S 迭代法 我们可以直接用Gauss-Seidel迭代法对基于自然顺序的离散Poisson方程(6.13)进行数值求解,即
算法6.6.求解二维离散Poisson方程的红黑排序G-S迭代法u ( 0 ) ∈ R N u^{(0)} \in \mathbb{R}^N u ( 0 ) ∈ R N i = 1 i = 1 i = 1 n n n j = 1 j = 1 j = 1 n n n u i , j ( k + 1 ) = 1 4 ( h 2 f i , j + u i + 1 , j ( k ) + u i − 1 , j ( k + 1 ) + u i , j + 1 ( k ) + u i , j − 1 ( k + 1 ) ) u_{i,j}^{(k + 1)} = \frac{1}{4}\left(h^2 f_{i,j} + u_{i + 1,j}^{(k)} + u_{i - 1,j}^{(k + 1)} + u_{i,j + 1}^{(k)} + u_{i,j - 1}^{(k + 1)}\right) u i , j ( k + 1 ) = 4 1 ( h 2 f i , j + u i + 1 , j ( k ) + u i − 1 , j ( k + 1 ) + u i , j + 1 ( k ) + u i , j − 1 ( k + 1 ) )
但此时迭代解的更新必须按自然顺序进行 (即更新 u i , j ( k + 1 ) u_{i,j}^{(k + 1)} u i , j ( k + 1 ) u i − 1 , j ( k + 1 ) u_{i - 1,j}^{(k + 1)} u i − 1 , j ( k + 1 ) u i , j − 1 ( k + 1 ) u_{i,j - 1}^{(k + 1)} u i , j − 1 ( k + 1 )
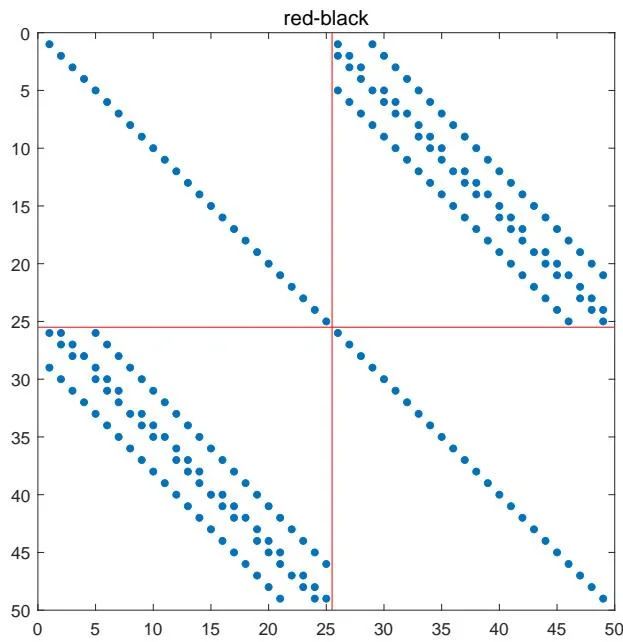
下面我们介绍一种适合并行计算的排序方法:红黑排序,即将二维网格点依次做红黑记号,如右图所示.
在计算过程中, 对 u i , j ( k + 1 ) u_{i,j}^{(k + 1)} u i , j ( k + 1 )
1: Given an initial guess u ( 0 ) ∈ R N u^{(0)} \in \mathbb{R}^N u ( 0 ) ∈ R N
3: for ( i , j ) (i,j) ( i , j ) u i , j ( k + 1 ) = 1 4 ( h 2 f i , j + u i + 1 , j ( k ) + u i − 1 , j ( k ) + u i , j + 1 ( k ) + u i , j − 1 ( k ) ) u_{i,j}^{(k + 1)} = \frac{1}{4}\left(h^2 f_{i,j} + u_{i + 1,j}^{(k)} + u_{i - 1,j}^{(k)} + u_{i,j + 1}^{(k)} + u_{i,j - 1}^{(k)}\right) u i , j ( k + 1 ) = 4 1 ( h 2 f i , j + u i + 1 , j ( k ) + u i − 1 , j ( k ) + u i , j + 1 ( k ) + u i , j − 1 ( k ) ) ( i , j ) (i,j) ( i , j ) u i , j ( k + 1 ) = 1 4 ( h 2 f i , j + u i + 1 , j ( k + 1 ) + u i − 1 , j ( k + 1 ) + u i , j + 1 ( k + 1 ) + u i , j − 1 ( k + 1 ) ) u_{i,j}^{(k + 1)} = \frac{1}{4}\left(h^2 f_{i,j} + u_{i + 1,j}^{(k + 1)} + u_{i - 1,j}^{(k + 1)} + u_{i,j + 1}^{(k + 1)} + u_{i,j - 1}^{(k + 1)}\right) u i , j ( k + 1 ) = 4 1 ( h 2 f i , j + u i + 1 , j ( k + 1 ) + u i − 1 , j ( k + 1 ) + u i , j + 1 ( k + 1 ) + u i , j − 1 ( k + 1 ) )
我们记基于红黑排序所得到的系数矩阵为 T N R B T_N^{\mathrm{RB}} T N RB 2 × 2 2\times 2 2 × 2 ( N = 7 2 ) (N = 7^{2}) ( N = 7 2 )
事实上, T N R B T_{N}^{\mathrm{RB}} T N RB T N T_{N} T N P P P
T N R B = P T N P ⊺ . T _ {N} ^ {\mathrm {R B}} = P T _ {N} P ^ {\intercal}. T N RB = P T N P ⊺ . 求解二维离散 Poisson 方程的 SOR 迭代法
算法6.7. 求解二维离散Poisson方程的SOR迭代法
1: Given an initial guess u ( 0 ) ∈ R N u^{(0)} \in \mathbb{R}^N u ( 0 ) ∈ R N ω \omega ω i = 1 i = 1 i = 1 n n n j = 1 j = 1 j = 1 n n n u i , j ( k + 1 ) = ( 1 − ω ) u i , j ( k ) + ω 4 ( h 2 f i , j + u i + 1 , j ( k ) + u i − 1 , j ( k + 1 ) + u i , j + 1 ( k ) + u i , j − 1 ( k + 1 ) ) u_{i,j}^{(k + 1)} = (1 - \omega)u_{i,j}^{(k)} + \frac{\omega}{4}\left(h^2 f_{i,j} + u_{i + 1,j}^{(k)} + u_{i - 1,j}^{(k + 1)} + u_{i,j + 1}^{(k)} + u_{i,j - 1}^{(k + 1)}\right) u i , j ( k + 1 ) = ( 1 − ω ) u i , j ( k ) + 4 ω ( h 2 f i , j + u i + 1 , j ( k ) + u i − 1 , j ( k + 1 ) + u i , j + 1 ( k ) + u i , j − 1 ( k + 1 ) )
8: end while A上面的SOR算法是基于自然排序,基于红黑排序的SOR算法请读者自己完成.
例6.2 已知二维Poisson方程
{ − Δ u ( x , y ) = − 1 , ( x , y ) ∈ Ω u ( x , y ) = x 2 + y 2 4 , ( x , y ) ∈ ∂ Ω \left\{ \begin{array}{l l} - \Delta u (x, y) = - 1, & (x, y) \in \Omega \\ u (x, y) = \frac {x ^ {2} + y ^ {2}}{4}, & (x, y) \in \partial \Omega \end{array} \right. { − Δ u ( x , y ) = − 1 , u ( x , y ) = 4 x 2 + y 2 , ( x , y ) ∈ Ω ( x , y ) ∈ ∂ Ω 其中 Ω = ( 0 , 1 ) × ( 0 , 1 ) \Omega = (0,1)\times (0,1) Ω = ( 0 , 1 ) × ( 0 , 1 ) u ( x , y ) = x 2 + y 2 4 u(x,y) = \frac{x^2 + y^2}{4} u ( x , y ) = 4 x 2 + y 2
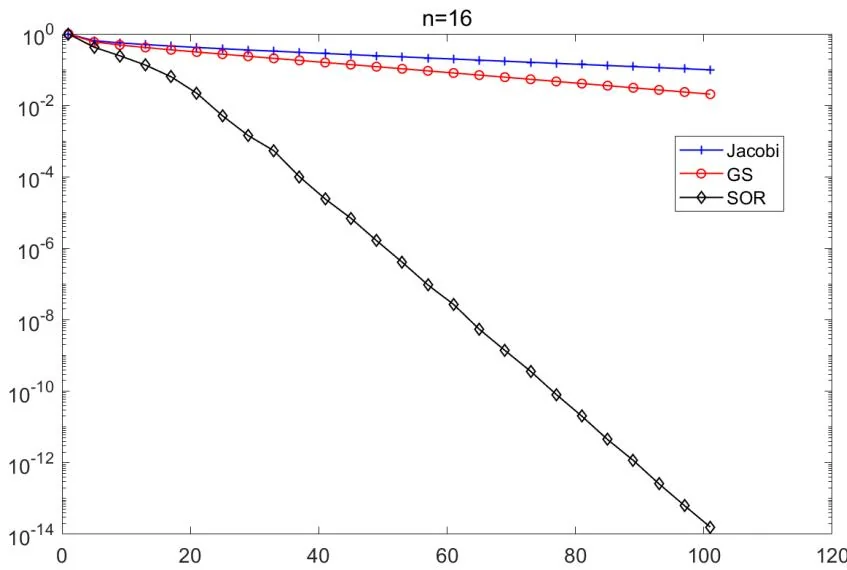
(1) 分别用 Jacobi, G-S 和 SOR 迭代法计算该方程组的解.ω \omega ω
解.(1)MATLAB程序参见Poisson_Jacobi_GS_SOR.m.定义近似解的相对误差:
relerr k ≜ ∥ u ( k ) − u ∗ ∥ 2 u ∗ , \operatorname {r e l e r r} _ {k} \triangleq \frac {\left\| u ^ {(k)} - u _ {*} \right\| _ {2}}{u _ {*}}, relerr k ≜ u ∗ u ( k ) − u ∗ 2 , 其中 u ∗ u_{*} u ∗ n = 16 n = 16 n = 16 N = 256 N = 256 N = 256
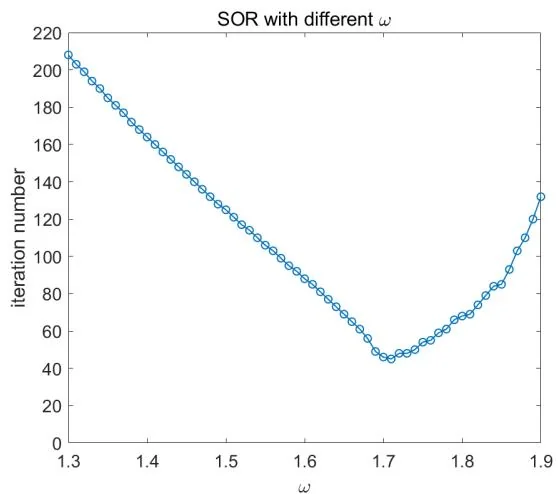
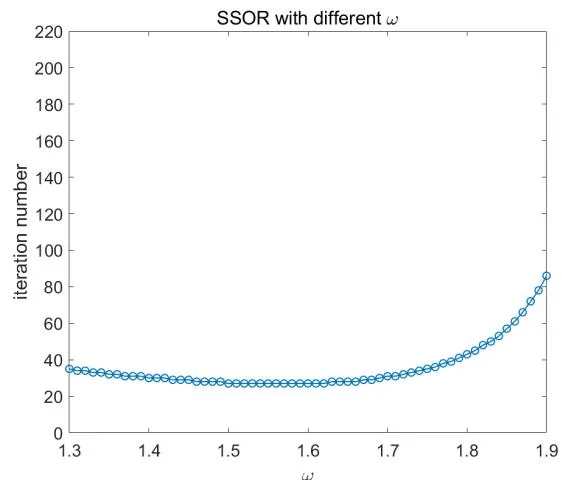
(2) MATLAB 程序参见 Poisson_SOR_omega.m 和 Poisson_SSOR_omega.m. 下图中画出了 n = 8 n = 8 n = 8 N = 64 N = 64 N = 64 ω \omega ω
ω \omega ω
6.3.3 收敛性分析 对于基本迭代法, 其收敛的充要条件是迭代矩阵的谱半径小于 1. 当谱半径不可求时, 我们可以根据迭代矩阵的范数来判断, 即如果迭代矩阵的某个范数小于 1, 则迭代法收敛.
本小节考虑求解二维离散 Poisson 方程的 Jacobi, G-S 和 SOR 的收敛性. 考虑这些方法的收敛性, 只需研究相应的迭代矩阵的谱半径即可. 对于二维离散 Poisson 方程, 系数矩阵为
A = T = I ⊗ T n + T n ⊗ I . A = T = I \otimes T _ {n} + T _ {n} \otimes I. A = T = I ⊗ T n + T n ⊗ I . 故 Jacobi 迭代法的迭代矩阵为
G J = D − 1 ( L + U ) = ( 4 I ) − 1 ( 4 I − T ) = I − T / 4. (6.21) G _ {\mathrm {J}} = D ^ {- 1} (L + U) = (4 I) ^ {- 1} (4 I - T) = I - T / 4. \tag {6.21} G J = D − 1 ( L + U ) = ( 4 I ) − 1 ( 4 I − T ) = I − T /4. ( 6.21 ) 由于 T T T
λ i + λ j = 2 ( 1 − cos π i n + 1 ) + 2 ( 1 − cos π j n + 1 ) = 4 − 2 ( cos π i n + 1 + cos π j n + 1 ) , \lambda_ {i} + \lambda_ {j} = 2 \left(1 - \cos \frac {\pi i}{n + 1}\right) + 2 \left(1 - \cos \frac {\pi j}{n + 1}\right) = 4 - 2 \left(\cos \frac {\pi i}{n + 1} + \cos \frac {\pi j}{n + 1}\right), λ i + λ j = 2 ( 1 − cos n + 1 πi ) + 2 ( 1 − cos n + 1 πj ) = 4 − 2 ( cos n + 1 πi + cos n + 1 πj ) , 所以 G J G_{\mathrm{J}} G J
1 − ( λ i + λ j ) / 4 = 1 2 ( cos π i n + 1 + cos π j n + 1 ) . 1 - \left(\lambda_ {i} + \lambda_ {j}\right) / 4 = \frac {1}{2} \left(\cos \frac {\pi i}{n + 1} + \cos \frac {\pi j}{n + 1}\right). 1 − ( λ i + λ j ) /4 = 2 1 ( cos n + 1 πi + cos n + 1 πj ) . 故
ρ ( G J ) = 1 2 max i , j { ∣ cos π i n + 1 + cos π j n + 1 ∣ } = cos π n + 1 < 1 , \rho (G _ {\mathrm {J}}) = \frac {1}{2} \max _ {i, j} \left\{\left| \cos \frac {\pi i}{n + 1} + \cos \frac {\pi j}{n + 1} \right| \right\} = \cos \frac {\pi}{n + 1} < 1, ρ ( G J ) = 2 1 i , j max { cos n + 1 πi + cos n + 1 πj } = cos n + 1 π < 1 , 即 Jacobi 迭代法是收敛的.
注意当 n n n κ ( T ) → ∞ \kappa (T)\to \infty κ ( T ) → ∞ T T T ρ ( G J ) → 1 \rho (G_{\mathrm{J}})\rightarrow 1 ρ ( G J ) → 1
通常, 问题越病态就越难求解, 舍入误差对解的影响也越大.
关于G-S和SOR,我们有下面的结论
定理6.27 设 G G S G_{\mathrm{GS}} G GS G S O R G_{\mathrm{SOR}} G SOR
ρ ( G G S ) = ρ ( G J ) 2 = cos 2 π n + 1 < 1 \rho (G _ {\mathrm {G S}}) = \rho (G _ {\mathrm {J}}) ^ {2} = \cos^ {2} \frac {\pi}{n + 1} < 1 ρ ( G GS ) = ρ ( G J ) 2 = cos 2 n + 1 π < 1 ρ ( G S O R ) = cos 2 π n + 1 ( 1 + sin π n + 1 ) 2 < 1 , ω = 2 1 + sin π n + 1 . \rho (G _ {\mathrm {S O R}}) = \frac {\cos^ {2} \frac {\pi}{n + 1}}{\left(1 + \sin \frac {\pi}{n + 1}\right) ^ {2}} < 1, \quad \omega = \frac {2}{1 + \sin \frac {\pi}{n + 1}}. ρ ( G SOR ) = ( 1 + sin n + 1 π ) 2 cos 2 n + 1 π < 1 , ω = 1 + sin n + 1 π 2 . 证明. 由于此时的系数矩阵 T N T_{N} T N
在上述结论中, SOR 中的 ω \omega ω ρ ( G S O R ) \rho(G_{\mathrm{SOR}}) ρ ( G SOR ) n n n
ρ ( G J ) = cos π n + 1 ≈ 1 − π 2 2 ( n + 1 ) 2 = 1 − O ( 1 n 2 ) , \rho (G _ {\mathrm {J}}) = \cos \frac {\pi}{n + 1} \approx 1 - \frac {\pi^ {2}}{2 (n + 1) ^ {2}} = 1 - O \left(\frac {1}{n ^ {2}}\right), ρ ( G J ) = cos n + 1 π ≈ 1 − 2 ( n + 1 ) 2 π 2 = 1 − O ( n 2 1 ) , ρ ( G S O R ) = cos 2 π n + 1 ( 1 + sin π n + 1 ) 2 ≈ 1 − 2 π n + 1 = 1 − O ( 1 n ) . \rho (G _ {\mathrm {S O R}}) = \frac {\cos^ {2} \frac {\pi}{n + 1}}{\left(1 + \sin \frac {\pi}{n + 1}\right) ^ {2}} \approx 1 - \frac {2 \pi}{n + 1} = 1 - O \left(\frac {1}{n}\right). ρ ( G SOR ) = ( 1 + sin n + 1 π ) 2 cos 2 n + 1 π ≈ 1 − n + 1 2 π = 1 − O ( n 1 ) . 由于当 n n n
( 1 − 1 n ) k ≈ 1 − k n = 1 − k n n 2 ≈ ( 1 − 1 n 2 ) k n , \left(1 - \frac {1}{n}\right) ^ {k} \approx 1 - \frac {k}{n} = 1 - \frac {k n}{n ^ {2}} \approx \left(1 - \frac {1}{n ^ {2}}\right) ^ {k n}, ( 1 − n 1 ) k ≈ 1 − n k = 1 − n 2 kn ≈ ( 1 − n 2 1 ) kn , 即SOR迭代 k k k k n kn kn n n n
需要指出的是, 对于一般线性方程组, 上述结论不一定成立.
由于 ρ ( G G S ) = ρ ( G J ) 2 \rho (G_{\mathrm{GS}}) = \rho (G_{\mathrm{J}})^2 ρ ( G GS ) = ρ ( G J ) 2
事实上, 当 n n n
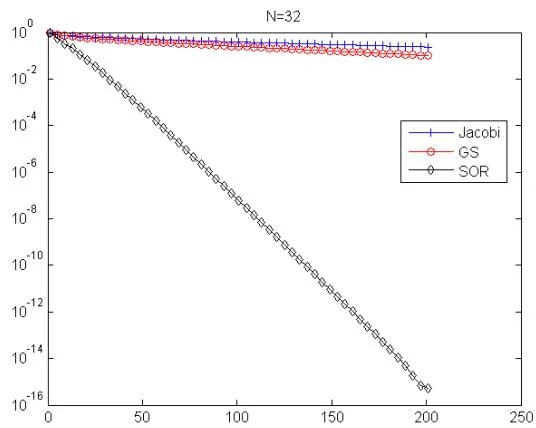
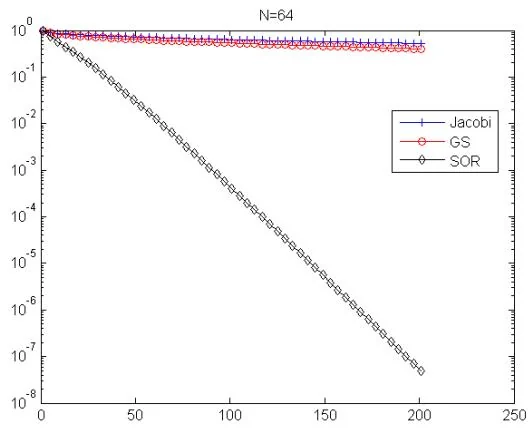
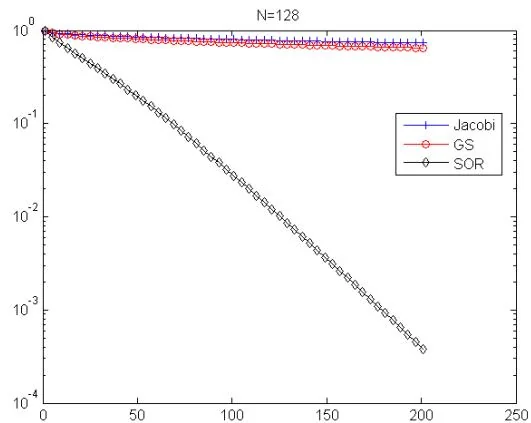
例6.3同例6.2,分别对不同的 n n n
解. 参见 MATLAB 程序 Poisson_Jacobi_GS_SOR_convergence.m. 下图中画出了 N = 16 , 32 , 64 , 128 N = 16,32,64,128 N = 16 , 32 , 64 , 128
事实上, 由于二维离散 Poisson 方程的系数矩阵 T N T_{N} T N T N T_{N} T N 0 < ω < 2 0 < \omega < 2 0 < ω < 2
6.3.4 快速求解方法 如果已经知道矩阵 A A A A = X Λ X − 1 A = X\Lambda X^{-1} A = X Λ X − 1 A x = b Ax = b A x = b
x = A − 1 b = X Λ − 1 X − 1 b . x = A ^ {- 1} b = X \Lambda^ {- 1} X ^ {- 1} b. x = A − 1 b = X Λ − 1 X − 1 b . 如果 A A A X X X
x = A − 1 b = X Λ − 1 X ∗ b . x = A ^ {- 1} b = X \Lambda^ {- 1} X ^ {*} b. x = A − 1 b = X Λ − 1 X ∗ b . 一般来说, 我们不会采用这种特征值分解的方法来解线性方程组, 因为计算特征值分解通常比解线性方程组更困难. 但在某些特殊情况下, 我们可以由此得到快速方法.
考虑二维离散 Poisson 方程
T u = h 2 f , (6.22) T u = h ^ {2} f, \tag {6.22} T u = h 2 f , ( 6.22 ) 其中
T = I ⊗ T n + T n ⊗ I , T n = tridiag ( − 1 , 2 , − 1 ) ∈ R n × n . T = I \otimes T _ {n} + T _ {n} \otimes I, \quad T _ {n} = \operatorname {t r i d i a g} (- 1, 2, - 1) \in \mathbb {R} ^ {n \times n}. T = I ⊗ T n + T n ⊗ I , T n = tridiag ( − 1 , 2 , − 1 ) ∈ R n × n . 由定理6.26可知
T = ( Z ⊗ Z ) ( I ⊗ Λ + Λ ⊗ I ) ( Z ⊗ Z ) T , T = (Z \otimes Z) (I \otimes \Lambda + \Lambda \otimes I) (Z \otimes Z) ^ {\mathsf {T}}, T = ( Z ⊗ Z ) ( I ⊗ Λ + Λ ⊗ I ) ( Z ⊗ Z ) T , 其中 Z = [ z 1 , z 2 , … , z n ] Z = [z_{1},z_{2},\ldots ,z_{n}] Z = [ z 1 , z 2 , … , z n ]
z k = 2 n + 1 [ sin k π n + 1 , sin 2 k π n + 1 , … , sin n k π n + 1 ] T , k = 1 , 2 , … , n . z _ {k} = \sqrt {\frac {2}{n + 1}} \left[ \sin \frac {k \pi}{n + 1}, \sin \frac {2 k \pi}{n + 1}, \ldots , \sin \frac {n k \pi}{n + 1} \right] ^ {\mathsf {T}}, \quad k = 1, 2, \ldots , n. z k = n + 1 2 [ sin n + 1 kπ , sin n + 1 2 kπ , … , sin n + 1 nkπ ] T , k = 1 , 2 , … , n . 所以,方程(6.15)的解为
u = T − 1 h 2 f = [ ( Z ⊗ Z ) ( I ⊗ Λ + Λ ⊗ I ) − 1 ( Z ⊗ Z ) ⊺ ] h 2 f . u = T ^ {- 1} h ^ {2} f = \left[ (Z \otimes Z) (I \otimes \Lambda + \Lambda \otimes I) ^ {- 1} (Z \otimes Z) ^ {\intercal} \right] h ^ {2} f. u = T − 1 h 2 f = [ ( Z ⊗ Z ) ( I ⊗ Λ + Λ ⊗ I ) − 1 ( Z ⊗ Z ) ⊺ ] h 2 f . 因此, 主要的运算是 Z ⊗ Z Z \otimes Z Z ⊗ Z ( Z ⊗ Z ) T (Z \otimes Z)^{\mathsf{T}} ( Z ⊗ Z ) T
快速Fourier变换 快速Fourier变换(FFT)是用来计算离散Fourier变换(DFT)矩阵与向量乘积的一种快速方法.
设 x = [ x 0 , x 1 … , x n − 1 ] ⊤ ∈ C n x = [x_0, x_1 \ldots, x_{n-1}]^\top \in \mathbb{C}^n x = [ x 0 , x 1 … , x n − 1 ] ⊤ ∈ C n y = D F T ( x ) = [ y 0 , y 1 … , y n − 1 ] ⊤ ∈ C n y = \mathrm{DFT}(x) = [y_0, y_1 \ldots, y_{n-1}]^\top \in \mathbb{C}^n y = DFT ( x ) = [ y 0 , y 1 … , y n − 1 ] ⊤ ∈ C n
y k = ∑ j = 0 n − 1 ω n k j x j , k = 0 , 1 , … , n − 1. y _ {k} = \sum_ {j = 0} ^ {n - 1} \omega_ {n} ^ {k j} x _ {j}, \quad k = 0, 1, \ldots , n - 1. y k = j = 0 ∑ n − 1 ω n kj x j , k = 0 , 1 , … , n − 1. 这里
ω n = e − 2 π i n = cos ( 2 π / n ) − i sin ( 2 π / n ) \omega_ {n} = e ^ {- \frac {2 \pi \mathbf {i}}{n}} = \cos (2 \pi / n) - \mathbf {i} \sin (2 \pi / n) ω n = e − n 2 π i = cos ( 2 π / n ) − i sin ( 2 π / n ) 是1的一个 n n n n n n i \mathbf{i} i
这里说 ω n \omega_{n} ω n n n n ω n n = 1 \omega_{n}^{n} = 1 ω n n = 1
ω n k ≠ 1 , k = 1 , 2 , … , n − 1. \omega_ {n} ^ {k} \neq 1, \quad k = 1, 2, \dots , n - 1. ω n k = 1 , k = 1 , 2 , … , n − 1. 构造矩阵 F n = [ f k j ] ∈ C n × n F_{n} = [f_{kj}]\in \mathbb{C}^{n\times n} F n = [ f kj ] ∈ C n × n f k j = ω n k j = e − 2 k j π i n = cos ( 2 k j π / n ) − i sin ( 2 k j π / n ) f_{kj} = \omega_n^{kj} = e^{-\frac{2kj\pi\mathbf{i}}{n}} = \cos (2kj\pi /n) - \mathbf{i}\sin (2kj\pi /n) f kj = ω n kj = e − n 2 kjπ i = cos ( 2 kjπ / n ) − i sin ( 2 kjπ / n )
F n = [ 1 1 1 … 1 1 ω n ω n 2 … ω n n − 1 1 ω n 2 ω n 4 … ω n 2 ( n − 1 ) ⋮ ⋮ ⋱ ⋮ 1 ω n n − 1 ω n 2 ( n − 1 ) … ω n ( n − 1 ) 2 ] , F _ {n} = \left[ \begin{array}{c c c c c} 1 & 1 & 1 & \dots & 1 \\ 1 & \omega_ {n} & \omega_ {n} ^ {2} & \dots & \omega_ {n} ^ {n - 1} \\ 1 & \omega_ {n} ^ {2} & \omega_ {n} ^ {4} & \dots & \omega_ {n} ^ {2 (n - 1)} \\ \vdots & \vdots & & \ddots & \vdots \\ 1 & \omega_ {n} ^ {n - 1} & \omega_ {n} ^ {2 (n - 1)} & \dots & \omega_ {n} ^ {(n - 1) ^ {2}} \end{array} \right], F n = 1 1 1 ⋮ 1 1 ω n ω n 2 ⋮ ω n n − 1 1 ω n 2 ω n 4 ω n 2 ( n − 1 ) … … … ⋱ … 1 ω n n − 1 ω n 2 ( n − 1 ) ⋮ ω n ( n − 1 ) 2 , 则有
y = D F T ( x ) = F n x . y = \mathrm {D F T} (x) = F _ {n} x. y = DFT ( x ) = F n x . 我们称矩阵 F n F_{n} F n
(1) F n F_{n} F n F n ∗ F n = n I F_{n}^{*}F_{n} = nI F n ∗ F n = n I 1 n F n \frac{1}{\sqrt{n}} F_{n} n 1 F n
相应的离散Fourier反变换定义为 x = I D F T ( y ) x = \mathrm{IDFT}(y) x = IDFT ( y )
x j = 1 n ∑ k = 0 n − 1 ω n − j k y k , j = 0 , 1 , … , n − 1. x _ {j} = \frac {1}{n} \sum_ {k = 0} ^ {n - 1} \omega_ {n} ^ {- j k} y _ {k}, \quad j = 0, 1, \ldots , n - 1. x j = n 1 k = 0 ∑ n − 1 ω n − jk y k , j = 0 , 1 , … , n − 1. 写成矩阵形式为
x = 1 n F ∗ y . x = \frac {1}{n} F ^ {*} y. x = n 1 F ∗ y . DFT和IDFT满足下面的性质:
I D F T ( D F T ( x ) ) = x , \mathrm {I D F T} (\mathrm {D F T} (x)) = x, IDFT ( DFT ( x )) = x , D F T ( I D F T ( y ) ) = y . \mathrm {D F T} (\mathrm {I D F T} (y)) = y. DFT ( IDFT ( y )) = y . 在MATLAB中,计算DFT和IDFT的函数分别为fft和ifft,即: y = f f t ( x ) , x = i f f t ( y ) y = \mathrm{fft}(x),x = \mathrm{ifft}(y) y = fft ( x ) , x = ifft ( y )
离散Sine变换 离散Sine变换(DST)有多种定义, 我们这里只介绍与求解 Poisson 方程有关的一种定义, 其它定义可参见[17].
设 x = [ x 1 , x 2 , … , x n ] T ∈ R n x = [x_{1},x_{2},\ldots ,x_{n}]^{\mathsf{T}}\in \mathbb{R}^{n} x = [ x 1 , x 2 , … , x n ] T ∈ R n y = D S T ( x ) = [ y 1 , y 2 , … , y n ] T ∈ R n y = \mathrm{DST}(x) = [y_1,y_2,\dots ,y_n]^{\mathsf{T}}\in \mathbb{R}^{n} y = DST ( x ) = [ y 1 , y 2 , … , y n ] T ∈ R n
y k = ∑ j = 1 n x j sin ( k j π n + 1 ) , k = 1 , 2 , … , n . y _ {k} = \sum_ {j = 1} ^ {n} x _ {j} \sin \left(\frac {k j \pi}{n + 1}\right), \quad k = 1, 2, \ldots , n. y k = j = 1 ∑ n x j sin ( n + 1 kjπ ) , k = 1 , 2 , … , n . 对应的离散Sine反变换记为IDST,即 x = I D S T ( y ) x = \mathrm{IDST}(\mathrm{y}) x = IDST ( y )
x j = 2 n + 1 ∑ k = 1 n y k sin ( j k π n + 1 ) , j = 1 , 2 , … , n . x _ {j} = \frac {2}{n + 1} \sum_ {k = 1} ^ {n} y _ {k} \sin \left(\frac {j k \pi}{n + 1}\right), \quad j = 1, 2, \dots , n. x j = n + 1 2 k = 1 ∑ n y k sin ( n + 1 jkπ ) , j = 1 , 2 , … , n . DST 和 IDST 满足下面的性质:
IDST ( DST ( x ) ) = x , \operatorname {I D S T} (\operatorname {D S T} (x)) = x, IDST ( DST ( x )) = x , D S T ( I D S T ( y ) ) = y . \mathrm {D S T} (\mathrm {I D S T} (y)) = y. DST ( IDST ( y )) = y . 在MATLAB中,计算DST和IDST的函数分别为dst和idst,即: y = d s t ( x ) , x = i d s t ( y ) y = \mathrm{dst}(x),x = \mathrm{idst}(y) y = dst ( x ) , x = idst ( y )
Possion方程与DST 我们首先考虑矩阵 Z Z Z b b b y = Z b y = Zb y = Z b
y k = ∑ j = 1 n Z ( k , j ) b j = 2 n + 1 ∑ j = 1 n b j sin ( k j π n + 1 ) = 2 n + 1 [ D S T ( b ) ] k , y _ {k} = \sum_ {j = 1} ^ {n} Z (k, j) b _ {j} = \sqrt {\frac {2}{n + 1}} \sum_ {j = 1} ^ {n} b _ {j} \sin \left(\frac {k j \pi}{n + 1}\right) = \sqrt {\frac {2}{n + 1}} \left[ \mathrm {D S T} (b) \right] _ {k}, y k = j = 1 ∑ n Z ( k , j ) b j = n + 1 2 j = 1 ∑ n b j sin ( n + 1 kjπ ) = n + 1 2 [ DST ( b ) ] k , 其中 [ D S T ( b ) ] k [\mathrm{DST}(b)]_k [ DST ( b ) ] k k k k y = Z b y = Zb y = Z b y = Z T b = Z − 1 b y = Z^{\mathsf{T}}b = Z^{-1}b y = Z T b = Z − 1 b
y = Z T b = Z − 1 b = ( 2 n + 1 ) − 1 I D S T ( b ) . y = Z ^ {\mathsf {T}} b = Z ^ {- 1} b = \left(\sqrt {\frac {2}{n + 1}}\right) ^ {- 1} \mathrm {I D S T} (b). y = Z T b = Z − 1 b = ( n + 1 2 ) − 1 IDST ( b ) . 所以对于一维离散 Poisson 方程, 其解为
u = T n − 1 ( h 2 f ) = ( Z Λ − 1 Z ⊺ ) ( h 2 f ) = h 2 Z Λ − 1 Z ⊺ f = h 2 D S T ( Λ − 1 I D S T ( b ) ) . u = T _ {n} ^ {- 1} (h ^ {2} f) = (Z \Lambda^ {- 1} Z ^ {\intercal}) (h ^ {2} f) = h ^ {2} Z \Lambda^ {- 1} Z ^ {\intercal} f = h ^ {2} \mathrm {D S T} (\Lambda^ {- 1} \mathrm {I D S T} (b)). u = T n − 1 ( h 2 f ) = ( Z Λ − 1 Z ⊺ ) ( h 2 f ) = h 2 Z Λ − 1 Z ⊺ f = h 2 DST ( Λ − 1 IDST ( b )) . 可以通过公式 T n = Z Λ Z ⊤ T_{n} = Z\Lambda Z^{\top} T n = Z Λ Z ⊤ [ α 1 , α 2 , … , α n ] ⊤ [\alpha_{1}, \alpha_{2}, \ldots, \alpha_{n}]^{\top} [ α 1 , α 2 , … , α n ] ⊤ [ β 1 , β 2 , … , β n ] ⊤ [\beta_{1}, \beta_{2}, \ldots, \beta_{n}]^{\top} [ β 1 , β 2 , … , β n ] ⊤ Z ⊤ T n Z^{\top}T_{n} Z ⊤ T n Z ⊤ Z^{\top} Z ⊤ T n T_{n} T n
λ i = α i β i . \lambda_ {i} = \frac {\alpha_ {i}}{\beta_ {i}}. λ i = β i α i . 对应的MATLAB代码为:Lam=idst([2,-1,zeros(1,n-2)]')./idst_eye(n,1))
而对于二维离散 Poisson 方程, 我们需要计算 ( Z ⊗ Z ) b (Z \otimes Z)b ( Z ⊗ Z ) b ( Z T ⊗ Z T ) b (Z^{\mathsf{T}} \otimes Z^{\mathsf{T}})b ( Z T ⊗ Z T ) b
设 b = [ b 1 T , b 2 T , … , b n T ] T ∈ R n 2 b = [b_1^{\mathsf{T}}, b_2^{\mathsf{T}}, \ldots, b_n^{\mathsf{T}}]^{\mathsf{T}} \in \mathbb{R}^{n^2} b = [ b 1 T , b 2 T , … , b n T ] T ∈ R n 2 b k ∈ R n × n b_k \in \mathbb{R}^{n \times n} b k ∈ R n × n B = [ b 1 , b 2 , … , b n ] ∈ R n × n B = [b_1, b_2, \ldots, b_n] \in \mathbb{R}^{n \times n} B = [ b 1 , b 2 , … , b n ] ∈ R n × n
( Z ⊗ Z ) b = ( Z ⊗ Z ) vec ( B ) = vec ( Z B Z ⊺ ) = vec ( ( Z ( Z B ) ⊺ ) ⊺ ) . (Z \otimes Z) b = (Z \otimes Z) \operatorname {v e c} (B) = \operatorname {v e c} (Z B Z ^ {\intercal}) = \operatorname {v e c} \left(\left(Z (Z B) ^ {\intercal}\right) ^ {\intercal}\right). ( Z ⊗ Z ) b = ( Z ⊗ Z ) vec ( B ) = vec ( ZB Z ⊺ ) = vec ( ( Z ( ZB ) ⊺ ) ⊺ ) . 因此, 我们仍然可以使用 DST 来计算 ( Z ⊗ Z ) b (Z \otimes Z)b ( Z ⊗ Z ) b ( Z T ⊗ Z T ) b (Z^{\mathsf{T}} \otimes Z^{\mathsf{T}})b ( Z T ⊗ Z T ) b
算法6.8.二维离散Poisson方程的快速方法 1: 计算 b = h 2 f b = h^{2}f b = h 2 f B = r e s h a p e ( b , n , n ) B = \mathrm{reshape}(b, n, n) B = reshape ( b , n , n ) B 1 = ( Z T B ) T = ( I D S T ( B ) ) T B_{1} = (Z^{\mathsf{T}}B)^{\mathsf{T}} = (\mathrm{IDST}(B))^{\mathsf{T}} B 1 = ( Z T B ) T = ( IDST ( B ) ) T B 2 = ( Z T B 1 ) T = ( I D S T ( B 1 ) ) T B_{2} = (Z^{\mathsf{T}}B_{1})^{\mathsf{T}} = (\mathrm{IDST}(B_{1}))^{\mathsf{T}} B 2 = ( Z T B 1 ) T = ( IDST ( B 1 ) ) T b 1 = ( I ⊗ Λ + Λ ⊗ I ) − 1 v e c ( B 2 ) b_{1} = (I \otimes \Lambda + \Lambda \otimes I)^{-1}\mathrm{vec}(B_{2}) b 1 = ( I ⊗ Λ + Λ ⊗ I ) − 1 vec ( B 2 ) B 3 = r e s h a p e ( b 1 , n , n ) B_{3} = \mathrm{reshape}(b_{1},n,n) B 3 = reshape ( b 1 , n , n ) B 4 = ( Z B 3 ) ⊤ = ( D S T ( B 3 ) ) ⊤ B_4 = (ZB_3)^\top = (\mathrm{DST}(B_3))^\top B 4 = ( Z B 3 ) ⊤ = ( DST ( B 3 ) ) ⊤ B 5 = ( Z B 4 ) T = ( D S T ( B 4 ) ) T B_{5} = (ZB_{4})^{\mathsf{T}} = (\mathrm{DST}(B_{4}))^{\mathsf{T}} B 5 = ( Z B 4 ) T = ( DST ( B 4 ) ) T u = reshape ( B 5 , n 2 , 1 ) u = \text{reshape}(B_5, n^2, 1) u = reshape ( B 5 , n 2 , 1 )
MATLAB 程序见 Poisson_DST.m
6.3.5 求解方法小结 由于 Poisson 方程的特殊结构和性质, 除了常规求解方法以外, 人们还设计出了一些特殊的快速算法. 下表列出了求解二维 Poisson 方程的不同方法的比较 [30], 这里假定网格剖分为 n × n n \times n n × n N = n 2 N = n^2 N = n 2