6.2 收敛性分析
6.2.1 基本概念
首先给出向量序列收敛的定义
定义6.2 (向量序列的收敛) 设 {x(k)}k=1∞ 是 Rn (或 Cn ) 中的一个向量序列. 如果存在向量 x=[x1,x2,…,xn]⊤∈Rn (或 Cn ) 使得
k→∞limxi(k)=xi,i=1,2,…,n, 其中 xi(k) 表示 x(k) 的第 i 个分量, 则称 {x(k)} (按分量) 收敛到 x , 即 x 是 x(k) 的极限, 记为
k→∞limx(k)=x. 类似地, 我们可以给出矩阵序列收敛的定义.
定义6.3 (矩阵序列的收敛) 设 {A(k)=[aij(k)]}k=0∞ 是 Rm×n (或 Cm×n ) 中的一个矩阵序列. 如果存在矩阵 A=[aij]∈Rm×n (或 Cm×n ) 使得
k→∞limaij(k)=aij,i=1,2,…,m,j=1,2,…,n, 则称 A(k) 收敛到 A , 即 A 是 A(k) 的极限, 记为
k→∞limA(k)=A. 关于向量序列和矩阵序列的收敛性, 我们有下面的基本判别方法 [144].
定理6.1 设向量序列 {x(k)}k=0∞⊂Rn (或 Cn ), 矩阵序列 {A(k)=[aij(k)]}k=0∞⊂Rm×n (或 Cm×n ), 则
(1) limk→∞x(k)=x⟺limk→∞∥x(k)−x∥=0, 其中 ∥⋅∥ 为任一向量范数;
(2) limk→∞A(k)=A⟺limk→∞∥A(k)−A∥=0, 其中 ∥⋅∥ 为任一矩阵范数;
(3) limk→∞A(k)=0⟺limk→∞A(k)x=0,∀x∈Rn (或 Cn)
由定理6.1和引理1.39,我们可以立即得到下面的结论
定理6.2 设矩阵 A∈Rn×n (或 Cn×n ), 则 limk→∞Ak=0 当且仅当 ρ(A)<1 . (板书)
证明. 充分性: 设 ρ(A)<1 , 则由引理 1.39 可知, 存在某个矩阵范数 ∥⋅∥ 使得 ∥A∥<1 . 因此由 0≤∥Ak∥≤∥A∥k→0(k→∞) 可得
k→∞lim∥Ak∥=0. 根据定理6.1,我们有 limk→∞Ak=0.
必要性:设 limk→∞Ak=0 ,则由定理6.1可知
k→∞lim∥Ak∥=0. 所以由 0≤ρ(A)k=ρ(Ak)≤∥Ak∥ 可得
k→∞limρ(A)k=0, 即 ρ(A)<1

下面给出谱半径与范数之间的一个重要关系式, 有时也用来定义矩阵的谱半径.
定理6.3 设 A∈Rn×n (或 Cn×n ), 则对任意矩阵范数 ∥⋅∥ , 有
ρ(A)=k→∞limAkk1. (板书)
证明. 由谱半径与范数之间的关系可知
ρ(A)k=ρ(Ak)≤∥Ak∥. 另一方面, 对任意 ε>0 , 构造矩阵
Aε=ρ(A)+ε1A. 则 ρ(Aε)<1 ,故 limk→∞Aεk=0 。因此存在正整数 N ,使得当 k>N 时,有 ∥Aεk∥<1 ,即
(ρ(A)+ε)kAk=(ρ(A)+ε)k∥Ak∥<1. 所以
ρ(A)≤Akk1≤ρ(A)+ε, 即对任意 ε>0 ,存在正整数 N ,使得当 k>N 时,有
Akk1−ρ(A)<ε. 根据极限定义可知, Akk1→ρ(A)

下面给出基本迭代法收敛的定义.
定义6.4 考虑基本迭代法(6.3),如果对任意的初始向量 x(0) ,都有
k→∞limx(k)→x∗, 则称基本迭代法 (6.3) 是收敛的, 否则就称其为发散的.
基于矩阵分裂的迭代法, 其收敛性取决于迭代矩阵的谱半径.
下面考虑基本迭代法 (6.3) 的收敛性. 首先给出一个迭代法收敛的充分条件.
引理6.4 若存在算子范数 ∥⋅∥ , 使得 ∥G∥<1 , 则迭代法 (6.3) 收敛.
(板书)
证明. 由 x(k+1)=Gx(k)+g 和 x∗=Gx∗+g 可得
x(k+1)−x∗=G(x(k)−x∗). 故
x(k+1)−x∗≤∥G∥x(k)−x∗. 依此类推, 可得
x(k+1)−x∗≤∥G∥k+1x(0)−x∗. 由于 ∥G∥<1 ,当 k→∞ 时,上式右端 →0 ,即 x(k+1)−x∗→0. 因此迭代法收敛.
事实上, 由习题1.10可知, 引理6.4条件中的算子范数可以改为任意矩阵范数
我们记 e(k)≜x(k)−x∗ 为第 k 步迭代解 x(k) 的误差向量.
定理 6.5 (基本收敛性定理) 对任意初始向量 x(0) , 迭代法 (6.3) 收敛的充要条件是 ρ(G)<1 . (板书)
证明. 必要性: 用反证法, 假设 ρ(G)≥1 . 设 λ 为 G 的模最大的特征值, 即 ∣λ∣=ρ(G)≥1 . 令 x=0 为其对应的特征向量. 取迭代初始向量 x(0)=x∗+x , 则
x(k)−x∗=G(x(k−1)−x∗)=⋯=Gk(x(0)−x∗)=Gkx=λkx, 不可能收敛到0,即方法不收敛.故假设不成立,因此 ρ(G)<1
充分性: 若 ρ(G)<1 , 则由引理 1.39 可知, 存在一个算子范数 ∥⋅∥ε , 使得 ∥G∥ε<1 . 再由引理 6.4 可知, 方法收敛. □
定义6.5 设 G 是迭代矩阵, 则迭代法 (6.3) 的平均收敛速度定义为
Rk(G)≜−ln∥Gk∥k1, 渐进收敛速度定义为
R(G)≜k→∞limRk(G)=−lnρ(G). 平均收敛速度与迭代步数和所用的范数有关, 但渐进收敛速度只依赖于迭代矩阵的谱半径.
数值分析中关于收敛速度的定义:
设点列 {εk}k=1∞ 收敛, 且 limk→∞εk=0 . 若存在一个有界常数 0<c<∞ , 使得
k→∞lim∣εk∣p∣εk+1∣=c, 则称点列 {εk} 是 p 次 (渐进) 收敛的. 若 1<p<2 或 p=1 且 c=0 , 则称点列是超线性收敛的.
定理6.6 考虑迭代法 (6.3). 如果存在某个算子范数 ∥⋅∥ 使得 ∥G∥=q<1 ,则
(1) ∥x(k)−x∗∥≤qk∥x(0)−x∗∥
(2) ∥x(k)−x∗∥≤1−qq∥x(k)−x(k−1)∥
(3) ∥x(k)−x∗∥≤1−qqk∥x(1)−x(0)∥
(板书)
证明. (1) 由 x(k)=Gx(k−1)+g 和 x∗=Gx∗+g 可得
x(k)−x∗=G(x(k−1)−x∗). 因此有
x(k)−x∗≤∥G∥⋅x(k−1)−x∗=q∥x(k−1)−x∗∥.(6.7) 反复利用结论 (\refeq:2) 即可得 ∥x(k)−x∗∥≤qk∥x(0)−x∗∥
(2) 由 x(k+1)=Gx(k)+g 和 x∗=Gx∗+g 可得
x(k+1)−x(k)=G(x(k)−x(k−1)) 因此有
x(k+1)−x(k)≤q∥x(k)−x(k−1)∥,(6.8) 根据 (\refeq:1) ,我们有 ∥x(k+1)−x∗∥≤q∥x(k)−x∗∥ .所以
x(k+1)−x(k)=x∗−x(k)+x(k+1)−x∗≥x∗−x(k)−x(k+1)−x∗≥(1−q)∥x(k)−x∗∥. 结合 (\refeq:1) 可得
∥x∗−x(k)∥≤1−q1∥x(k+1)−x(k)∥≤1−qq∥x(k)−x(k−1)∥. (3) 反复利用 (\refeq:1) 即可得
x(k+1)−x(k)≤qkx(1)−x(0). 所以
∥x∗−x(k)∥≤1−q1∥x(k+1)−x(k)∥≤1−qqk∥x(1)−x(0)∥. 
一般来说,好的迭代法应该满足[30]:
(1) ρ(G) 很小;
(2) 以 M 为系数矩阵的线性方程组比较容易求解
6.2.2 不可约对角占优矩阵
这里我们考虑 A 是严格对角占优或不可约对角占优情形
定理6.7 设 A∈Rn×n , 若 A 严格对角占优, 则 Jacobi 迭代法和 G-S 迭代法都收敛, 且
∥GGS∥∞≤∥GJ∥∞<1. (板书)
证明. 首先证明 ∥GJ∥∞<1 . 由于 A 严格行对角占优, 故 ∑j=i∣aij∣/∣aii∣<1 . 所以
∥GJ∥∞=∥D−1(L+U)∥∞=1≤i≤nmaxj=i∑∣aii∣∣aij∣<1. 下面证明 ∥GGS∥∞≤∥GJ∥∞ ,只需证明 ∣GGS∣e≤∣GJ∣e 即可,其中 e=[1,1,…,1]T
令 L~=D−1L 和 U~=D−1U . 则 L~ 是严格下三角矩阵, 故 L~n=0 , 所以
(I−L~)−1=I+L~+L~2+⋯+L~n−1. 于是
∣GGS∣e=∣(D−L)−1U∣e=∣(I−L~)−1U~∣e=∣(I+L~+L~2+⋯+L~n−1)U~∣e≤(I+∣L~∣+∣L~∣2+⋯+∣L~∣n−1)∣U~∣e=(I−∣L~∣)−1∣U~∣e.(6.9) 由 A 的严格行对角占优性可知 1−∑j=i∣aii∣∣aij∣>0, 即 (I−∣L~∣−∣U~∣)e>0. 两边同乘 ∣L~∣≥0 可得
0≤∣L~∣(I−∣L~∣−∣U~∣)e=(∣L~∣−∣L~∣2+∣U~∣−∣L~∣⋅∣U~∣−∣U~∣)e=((I−∣L~∣)(∣L~∣+∣U~∣)−∣U~∣)e, 即 ∣U~∣e≤(I−∣L~∣)(∣L~∣+∣U~∣)e. 两边同乘 (I−∣L~∣)−1≥0 可得
(I−∣L~∣)−1∣U~∣e≤(∣L~∣+∣U~∣)e. 又 ∣L~∣+∣U~∣=∣D−1(L+U)∣=∣GJ∣ , 由 (6.9) 可知 ∣GGS∣e≤∣GJ∣e , 即定理结论成立.
当 A 是严格列对角占优时, 该结论也成立.
定理6.8 设 A∈Rn×n , 若 A 不可约对角占优, 则 Jacobi 迭代法和 G-S 迭代法都收敛. 进一步, 若 A 是非负矩阵, 则
ρ(GGS)<ρ(GJ)<1. (留作课外自习, 需利用非负矩阵的相关知识, 可参见 [139])
思考:若 A∈Rn×n 严格对角占优且非负,则是否有结论 ρ(GGS)≤ρ(GJ)?
上述定理中的结论对一般矩阵并不成立:对某些矩阵,Jacobi迭代法收敛,但G-S迭代法却不一定收敛,见思考题6.23.
关于SOR迭代法,我们有下面的结论
定理6.9 设 A∈Rn×n , 若 A 严格对角占优且 0<ω≤1 , 则SOR迭代法收敛.
(板书)
证明. 反证法. 假设SOR迭代法不收敛, 即 ρ(GSOR)≥1 . 因此 GSOR 存在特征值 λ , 满足 ∣λ∣≥1 . 由 det(λI−GSOR)=0 可知
det(λI−(D−ωL)−1((1−ω)D+ωU))=det((D−ωL)−1)⋅det(λ(D−ωL)−(1−ω)D−ωU)=det((D−ωL)−1)⋅det((λ+ω−1)D−λωL−ωU)=0. 又 det((D−ωL)−1)=0 ,所以
det((λ+ω−1)D−λωL−ωU)=0. 由 0<ω≤1 和 ∣λ∣≥1 可知, λ+ω−1=0 . 所以 det(G~)=0 , 其中
G~=D−λ+ω−1λωL−λ+ω−1ωU.(6.10) 令 λ=a+ib ,其中 a,b∈R .则根据 0<ω≤1 和 ∣λ∣≥1 ,可得
∣λ+ω−1∣2−∣λω∣2=(a+ω+1)2+b2−ω2(a2+b2)=(1−ω)((a−1)2+ω(a2+b2−1)+b2)≥0.(6.11) 所以
∣λ+ω−1∣∣ω∣≤∣λ+ω−1∣∣λω∣≤1. 又 A 是严格对角占优的, 所以由 (6.10) 和 (6.11) 可知, G~ 也严格对角占优. 这意味着 det(G~)=0 , 矛盾.
定理6.10 设 A∈Rn×n , 若 A 不可约对角占优且 0<ω≤1 , 则SOR迭代法收敛.
(留作课外自习)
6.2.3 对称正定矩阵
首先给出Richardson迭代法的收敛性
定理6.11 设 A∈Rn×n 是对称正定矩阵, λ1 和 λn 分别是 A 的最大和最小特征值, 则Richardson迭代法收敛当且仅当
0<ω<λ12. 另外, Richardson 迭代法的最优参数为
ω∗=argωminρ(GR)=λ1+λn2, 即当 ω=ω∗ 时,迭代矩阵的谱半径达到最小,并且有
ρ(GR)=⎩⎨⎧1−ωλn,λ1+λnλ1−λn=κ(A)+1κ(A)−1,ωλ1−1,i fω≤ω∗,i fω=ω∗,i fω≥ω∗. (留作练习)
下面考虑 Jacobi, Gauss-Seidel 和 SOR 的收敛性, 先介绍两个引理.
引理6.12 设 A∈Cn×n 是Hermite的, 矩阵分裂 A=M−N , 其中 M 非奇异, 则 M∗+N 也是Hermite的, 且对任意 x∈Cn 有
x∗Ax−x~∗Ax~=u∗(M∗+N)u, 其中 x~=M−1Nx,u=x−x~
(板书)
证明. 由于 A 是Hermite的, 所以 M∗+N=M∗+M−A 也是Hermite的.
由于 x~=M−1Nx ,所以 Mx~=Nx ,因此
Mu=Mx−Mx~=Mx−Nx=Ax, Nu=Nx−Nx~=Mx~−Nx~=Ax~. 由 M∗+N 的对称性可知 M=M∗+N−N∗ 又 (Nx)∗=(Mx~)∗ ,所以
x∗Ax−x~∗Ax~=x∗Mu−x~∗Nu=x∗(M∗+N−N∗)u−x~∗Nu=x∗M∗u−x∗N∗u+x∗Nu−x~∗Nu=x∗M∗u−x~∗M∗u+u∗Nu=u∗(M∗+N)u. 
引理6.13 设 A∈Rn×n 对称, 矩阵分裂 A=M−N 满足 M⊤+N 正定, 则 ρ(M−1N)<1 当且仅当 A 是正定的. (板书)
证明. 充分性. 设 λ∈C 是 M−1N 的一个特征值, 对应的特征向量为 x=0 , 即
M−1Nx=λx. 我们首先说明 λ=1 假设 λ=1 ,则可得 Mx=Nx ,即 Ax=0 .由于 A 非奇异,所以 x=0 ,矛盾.
令 x~=M−1Nx=λx,u=x−x~=(1−λ)x. 则由引理6.12可得
(1−∣λ∣2)x∗Ax=∣1−λ∣2x∗(M⊺+N)x. 由于 A 和 MT+N 都是正定矩阵, 所以上式右端为正, 故 ∣λ∣<1 . 因此 ρ(M−1N)<1 .
必要性. 反证法. 假设 A 不是正定的. 由于 ρ(M−1N)<1 , 所以 A=M(I−M−1N) 非奇异, 因此存在 x(0)∈Rn , 使得
η≜(x(0))⊺Ax(0)<0. 以 x(0) 为初始点,构造迭代序列
x(k)=M−1Nx(k−1),k=1,2,…. 由 ρ(M−1N)<1 可知
k→∞limx(k)=k→∞lim(M−1N)kx(0)=0.(6.12) 令 u(k)=x(k−1)−x(k) ,则由引理6.12可得
(x(k−1))TAx(k−1)−(x(k))TAx(k)=(u(k))T(MT+N)u(k). 由于 MT+N 对称正定, 上式右端非负, 所以
(x(k))TAx(k)≤(x(k−1))TAx(k−1). 依此类推, 可得
(x(k))⊤Ax(k)≤(x(0))⊤Ax(0)=η<0. 这与 (6.12) 矛盾. 因此 A 一定是正定的

我们首先给出SOR迭代法收敛的一个必要条件
定理6.14 对于SOR迭代法,有 ρ(GSOR)≥∣1−ω∣ ,故SOR迭代法收敛的必要条件是 0<ω<2 (板书)
证明.SOR的迭代矩阵为
GSOR=(D−ωL)−1((1−ω)D+ωU)=(I−ωL~)−1((1−ω)I+ωU~). 所以 GSOR 的行列式为
det(GSOR)=det((I−ωL~)−1)⋅det((1−ω)I+ωU~)=(1−ω)n. 设 GSOR 的特征为 λ1,λ2,…,λn ,则
λ1λ2…λn=det(GSOR)=(1−ω)n, 故至少有一个特征值的模不小于 ∣1−ω∣ , 即 ρ(GSOR)≥∣1−ω∣ .
若SOR收敛,则 ρ(GSOR)<1 ,因此 ∣1−ω∣<1 ,即 0<ω<2

定理6.15 设 A∈Rn×n 对称正定
(1) 若 2D−A 正定, 则 Jacobi 迭代法收敛.
(2) 若 0<ω<2 ,则SOR迭代法和SSOR迭代法收敛
(3) G-S 迭代法收敛.
(留作课外自习, 直接利用前面的引理即可)
定理6.16 设 A∈Rn×n 对称, 且 D 正定
(1) 若 Jacobi 迭代法收敛, 则 A 和 2D−A 都正定;
(2) 若存在 ω∈(0,2) 使得 SOR (或 SSOR) 迭代法收敛, 则 A 正定;
(3) 若 G-S 迭代法收敛, 则 A 正定.
(板书, 只证明 (1), (2) 和 (3) 利用引理 6.13 即可)
证明. 设 Jacobi 迭代收敛. 由于 A 对称, D 对称正定, 所以 D−1A=D−21(D−21AD−21)D21 的特征值都是实数. 又
GJ=D−1(D−A)=I−D−1A, 由 ρ(GJ)<1 可知 λ(D−1A)>0 ,即 λ(D−21AD−21)>0, 所以 λ(A)>0, 故 A 正定.
下面证明 2D−A 的正定性. 根据 ρ(GJ)<1 可知
0<λ(D−1A)<2, 所以
0<λ(2I−D−1A)<2. 又 2D−A 与 D−21(2D−A)D−21 合同, 而
D−21(2D−A)D−21=2I−D−21AD−21=D21(2I−D−1A)D−21, 即 D−21(2D−A)D−21 与 2I−D−1A 有相同的特征值, 所以 2D−A 的特征值也都是正数, 即 2D−A 正定. □
推论6.17 设 A∈Rn×n 对称且 D 正定, 则
(1) Jacobi 收敛的充要条件是 A 和 2D−A 都正定;
(2) G-S 收敛的充要条件是 A 正定;
(3)SOR收敛的充要条件是 A 正定且 ω∈(0,2)
6.2.4 相容次序矩阵*
针对一类特殊的矩阵, Jacobi 迭代矩阵和 SOR 迭代矩阵的特征值之间存在一种特殊的关系式, 根据这个关系式, 在某些场合下就可以确定 SOR 的最优参数的取值.
定义6.6设 A∈Rn×n 的对角线元素全不为零,记 L~=D−1L,U~=D−1U ,即 A=D(I−L~−U~) 若矩阵 G(α)≜αL~+α1U~ 的特征值与 α 无关 (α=0) ,则称 A 是相容次序矩阵 (consistentlyordered matrix).
下面我们讨论一类特殊的相容次序矩阵. 首先给出一个引理
引理6.18 设 B∈Rn×n 具有下面的结构
B=[0B21B120],其 中B12∈Rk×(n−k),B21∈R(n−k)×k,0≤k≤n. 令 BL 和 BU 分别表示 B 的下三角和上三角部分, 则
(1) 若 μ 是 B 的特征值, 则 −μ 也是 B 的特征值;
(2) B(α) 的特征值与 α 无关, 其中
B(α)=αBL+α1BU,α=0. (板书)
证明. (1) 若 [x,y] 是 B 的对应于 μ 的特征向量, 则 [x,−y] 是 B 对应于 −μ 的特征向量.
(2) 由于 α=0 , 我们有
[I00αI]−1B(α)[I00αI]=[I00α1I][0αB21α1B120][I00αI]=[0B21B120], 故引理结论成立.
该结论对复矩阵也成立.
由引理6.18中结论(2)可知, B(α)+βI 的特征值也与 α 无关,其中 β 为任意常数
定义6.7 设 A∈Rn×n , 如果存在一个置换矩阵 P , 使得
PAPT=[D1EFD2],(6.13) 其中 D1,D2 为对角矩阵, 则称 A 具有性质 A .
性质A意味着指标集 Zn={1,2,…,n} 可以分成两个互不相交的子集之和,在同一个子集内的未知量相互独立,因此在迭代更新时可以并行计算. (也就是说, Zn=S∪T,S∩T=∅ 当 i=j 且 i,j∈S 或 i,j∈T 时,有 aij=0. )
相容次序矩阵和性质A有不同的定义方式,我们这里采用的是Demmel(1997)[30]中的定义.其他定义可参见Varga(1962,2000)[139]或Young(1971)[141].事实上,根据Axelsson(1994)[6, page 239]中的说法,Yong(1950)[140]也是按照定义6.6和定义6.7来定义相容次序矩阵和性质A的.
根据引理6.18, 我们可以直接得到下面的结论
定理 6.19 设 A 的对角线元素全不为零, 若 A 具有性质 A, 则存在置换矩阵 P , 使得 PAP⊤ 是相容次序矩阵.
如果矩阵 A 本身就具有(6.7)的形式, 则 A 就是相容次序矩阵
事实上, (6.7) 可推广到分块三对角矩阵情形, 见下面的例子.
例6.1 设 Di 是非奇异的对角矩阵, 则任意块三对角矩阵
D1B1A1⋱⋱⋱⋱BN−1AN−1DN 都是相容次序矩阵
(留作练习, 参见 [141])
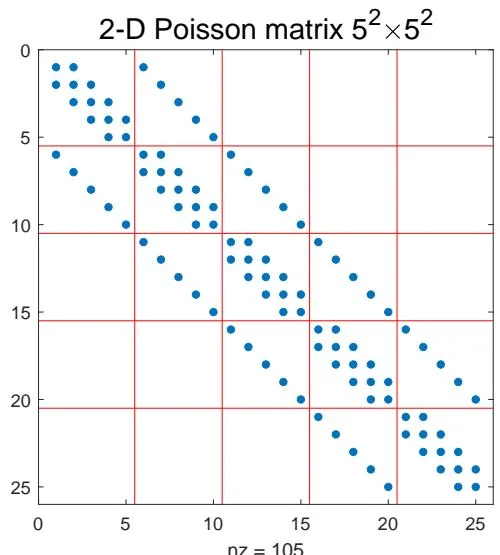
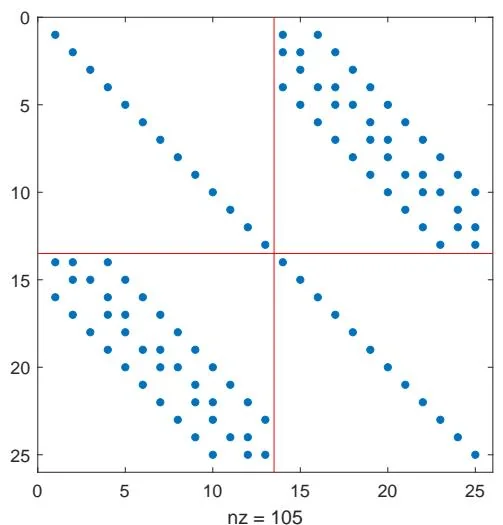
用有限差分法离散的二维偏微分方程(左图是网格点自然排序, 右图是红黑排序)
定理6.20 设 A 是相容次序矩阵且 ω=0 , 则下列命题成立
(1) Jacobi迭代矩阵 GJ 的特征值正负成对出现;
(2) 若 μ 是 GJ 的一个特征值且 λ 满足
(λ+ω−1)2=λω2μ2,(6.14) 则 λ 是SOR迭代矩阵 GSOR 的特征值;
(3) 反之, 若 λ=0 是 GSOR 的一个特征值且 μ 满足 (6.8), 则 μ 是 GJ 的特征值.
(板书)
证明. (1) 易知 GJ=G(1) . 设 μ 是 G(1) 的特征值, 因为 G(−1)=−G(1) , 所以 −μ 是 G(−1) 的特征值. 又 G(α) 的特征值与 α 无关, 故 −μ 也是 G(1) 的特征值, 所以命题结论成立.
(2) 若 λ=0 , 则由 (6.8) 可知 ω=1 , 此时 GSOR=(I−L~)−1U~ 为奇异矩阵, 故 λ=0 是其特征值, 即命题结论成立.
若 λ=0 ,则 GSOR 的特征多项式为
det(λI−GSOR)=det(λI−(I−ωL~)−1((1−ω)I+ωU~))=det((I−ωL~)−1)⋅det(λ(I−ωL~)−(1−ω)I−ωU~)=det((λ+ω−1)I−λωL~−ωU~) =det(λω2((λω2λ+ω−1)I−λL~−λ1U~))=(λω2)n/2det((λω2λ+ω−1)I−L~−U~),(6.15) 其中最后一个等式由引理6.18推得. 令
μ=λω2λ+ω−1即(λ+ω−1)2=λω2μ2, 则由 (6.14) 和性质(1)可知 λ 是 GSOR 的特征值当且仅当 μ 是 GJ=L~+U~ 的特征值,即命题结论成立.
(3) 已经由 (2) 证明.

推论6.21设 A 是相容次序矩阵.若 GJ 的特征值全部为实数,则SOR迭代法收敛的充要条件是 0<ω<2 且 ρ(GJ)<1. (留作练习)
推论6.22 若 A 是相容次序矩阵, 则 ρ(GGS)=ρ(GJ)2 , 即当 Jacobi 迭代法收敛时, Gauss-Seidel 迭代法比 Jacobi 迭代法快一倍.
下面是关于SOR迭代法的最优参数选取
定理6.23 设 A 是相容次序矩阵。若 GJ 的特征值全部为实数,且 ρJ≜ρ(GJ)<1 ,则SOR迭代法的最优参数为
ωopt=1+1−ρJ22, 此时
ρ(GSOR)=ωopt−1=(1+1−ρJ2)2ρJ2. 进一步, 有
ρ(GSOR)={ω−1,1−ω+21ω2ρJ2+ωρJ1−ω+41ω2ρJ2,ωopt≤ω≤20<ω≤ωopt. (留作课外自习, 直接求解等式 (6.8), 分情况讨论即可, 可参见 [141, page 173])








