5.3_共享内存和同步

5.3 共享内存和同步

到目前为止，将线程块分解为线程的目的只是为了解决线程块数量的硬件限制。这是一个很勉强的动机，因为这完全可以由CUDA运行时在幕后自动完成。显然，还有其他的原因需要将线程块分解为多个线程。

CUDA C支持共享内存。这块内存引出了对于C语言的另一个扩展，这个扩展类似于__device__和__global__。在编写代码时，你可以将CUDA C的关键字__share__添加到变量声明中，这将使这个变量驻留在共享内存中。那么，这么做的目的是什么？

很高兴你能问这个问题。CUDA C编译器对共享内存中的变量与普通变量将分别采取不同的处理方式。对于在GPU上启动的每个线程块，CUDA C编译器都将创建该变量的一个副本。线程块中的每个线程都共享这块内存，但线程却无法看到也不能修改其他线程块的变量副本。这就实现了一种非常好的方式，使得一个线程块中的多个线程能够在计算上进行通信和协作。

而且，共享内存缓冲区驻留在物理GPU上，而不是驻留在GPU之外的系统内存中。因此，在访问共享内存时的延迟要远远低于访问普通缓冲区的延迟，使得共享内存像每个线程块的高速缓存或者中间结果暂存器那样高效。

线程之间相互通信的功能或许已经令你很兴奋了，这个功能同样也使我们感到兴奋。但世上没有免费的东西，线程间的通信也不例外。如果想要在线程之间进行通信，那么还需要一种机制来实现线程之间的同步。例如，如果线程A将一个值写入到共享内存，并且我们希望线程B对这个值进行一些操作，那么只有当线程A的写入操作完成之后，线程B才能开始执行它的操作。如果没有同步，那么将发生竞态条件（Race Condition），在这种情况下，代码执行结果的正确性将取决于硬件的不确定性。

我们来看一个使用这些功能的示例。

5.3.1 点积运算

恭喜你！我们已经学习完了矢量的加法运算，接下来将介绍矢量的点积运算（Dot Product，也称为内积）。我们将快速介绍点积运算的过程，以免你不熟悉这种矢量运算（或者还是早在几年前学过）。这个计算包含两个步骤。首先，将两个输入矢量中相应的元素相乘。这非常类似于矢量的加法运算，只不过在这里使用的是乘法而不是加法。然而，在计算完这个步骤后，不是将值保存到第三个输出矢量中，而是将这些值相加起来以得到一个标量输出值。

例如，如果对两个包含4个元素的矢量进行点积运算，那么计算公示如5.1所示。

等式5.1

(x1,x2,x3,x4)⋅(y1,y2,y3,y4)=x1y1+x2y2+x3y3+x4y4\left(x _ {1}, x _ {2}, x _ {3}, x _ {4}\right) \cdot \left(y _ {1}, y _ {2}, y _ {3}, y _ {4}\right) = x _ {1} y _ {1} + x _ {2} y _ {2} + x _ {3} y _ {3} + x _ {4} y _ {4}

你或许已经理解了我们将要使用的算法。首先，可以像矢量加法那样，每个线程将两个相应的元素相乘，然后移动到下两个元素。由于最终的结果是所有乘积的总和，因此每个线程还要保存它所计算的乘积的加和。与矢量加法示例一样，线程每次对索引的增加值为线程的数量，这样能确保不会遗漏任何元素，而且也不会将任何元素相乘两次。下面的代码实现了点积函数的第一个步骤：

include"../common/book.h"   
#defineimin(a,b)  $(a <   b?a:b)$    
const int N  $= 33$  \*1024;   
const int threadsPerBlock  $= 256$  .   
__global__void dot(float \*a,float \*b,float \*c）{
__shared__ float cache threadsPerBlock;  
int tid = threadIdx.x + blockIdx.x * blockDim.x;  
int cacheIndex = threadIdx.x;  
float temp = 0;  
while (tid < N) {  
    temp += a[tid] * b[tid];  
    tid += blockDim.x * gridDim.x;  
}  
//设置cache中相应位置上的值  
cache[cacheIndex] = temp;

在代码中声明了一个共享内存缓冲区，名字为cahe。这个缓冲区将保存每个线程计算的加和值。我们稍后会看到为什么要这么做，但现在只分析在实现第一个步骤时采用的方法。要声明一个驻留在共享内存中的变量是很容易的，这相当于在标准C中声明一个static或volatile类型的变量。

\_shared\_ float cache[threadsPerBlock];

我们将数组的大小声明为threadsPerBlock，这样线程块中的每个线程都能将它计算的临时结果保存到某个位置上。之前在分配全局内存时，我们为每个执行核函数的线程都分配了足够的内存，即线程块的数量乘以threadPerBlock。但对于共享变量来说，由于编译器将为每个线程块生成共享变量的一个副本，因此只需根据线程块中线程的数量来分配内存。

在分配了共享内存后，像前面一样计算数据索引：

int tid = threadIdx.x + blockIdx.x * blockDim.x;  
int cacheIndex = threadIdx.x;

现在，你应该对变量tid的计算很熟悉了，通过线程块索引和线程索引计算出输入数组中的一个全局偏移。共享内存缓存中的偏移就等于线程索引。线程块索引与这个偏移无关，因为每个线程块都拥有该共享内存的私有副本。

最后，我们设置了共享内存缓冲区相应位置上的值，以便随后能将整个数组相加起来，并且无需担心某个特定的位置上是否包含有效的数据：

//设置cache中相应位置上的值  
cache[cacheIndex] = temp;

如果输入矢量的长度不是线程块中线程数量的整数倍，那么cache中的元素将不会被全部用到。在这种情况中，最后一个线程块中将有一些线程不做任何事情。

每个线程都计算数组a和b中相应元素乘积的总和，然后当到达数组末尾时，再将临时加和值保存到共享缓冲区中。

float temp = 0;  
while (tid < N) {  
    temp += a[tid] * b[tid];  
    tid += blockDim.x * gridDim.x;  
}
//设置cache中相应位置上的值cache[cacheIndex]  $\equiv$  temp;

当算法执行到这一步时，我们需要将cache中所有的值相加起来。在执行这个运算时，需要通过一个线程来读取保存在cache中的值。然而，在前面已经提到过，这可能是一种危险的操作。我们需要某种方法来确保所有对共享数组cache[]的写入操作在读取cache之前完成。幸运的是，这种方法确实存在：

//对线程块中的线程进行同步__syncthreads();

这个函数调用将确保线程块中的每个线程都执行完__syncthreads()前面的语句后，才会执行下一条语句。这正是我们需要的功能。现在，我们知道，当一个线程执行__syncthreads()后面的第一条语句时，线程块中的其他线程肯定都已经执行完了__syncthreads()。

这时，我们可以确信cache已经填好了，因此可以将其中的值相加起来。这个相加过程可以抽象为更一般的形式：对一个输入数组执行某种计算，然后产生一个更小的结果数组，这种过程也称为归约（Reduction）。在并行计算中经常会遇到类似的运算，因此人们专门为这类算法起了一个名字。

实现归约运算的最简单方法是，由一个线程在共享内存上进行迭代并计算出总和值。计算的时间与数组的长度成正比。然而，在这里的示例中有数百个线程可用，因此我们可以以并行方式来执行归约运算，这样所花的时间将与数组长度的对数成正比。初看上去，下面的代码有些费解，我们将在随后对其进行分析。

代码的基本思想是，每个线程将cache[]中的两个值相加起来，然后将结果保存回cache[]。由于每个线程都将两个值合并为一个值，那么在完成这个步骤后，得到的结果数量就是计算开始时数值数量的一半。在下一个步骤中，我们对这一半数值执行相同的操作。在将这种操作执行log2 threadsPerBlock)个步骤后，就能得到cache[]中所有值的总和。对这里的示例来说，我们在每个线程块中使用了256个线程，因此需要8次迭代将cache[]中的256个值归约为1个值。

实现这个归约运算的代码如下所示：

// 对于归约运算来说，以下代码要求threadPerBlock必须是2的指数int i = blockDim.x/2;  
while (i != 0) {
if (cacheIndex < i)  
    cache[cacheIndex] += cache[cacheIndex + i];  
    __syncreads();  
    i /= 2;

在第一个步骤中，我们取threadsPerBlock的一半作为i值，只有索引小于这个值的线程才会执行。只有当线程的索引小于i时，才可以把cache[]的两个数据项相加起来，因此我们将加法运算放在if(cacheIndex < i)的代码块中。执行加法运算的线程将cache[]中线程索引位置上的值和线程索引加上i得到的位置上的值相加起来，并将结果保存回cache[]中线程索引位置上。

假设在cache[]中有8个元素，因此i的值为4。归约运算的其中一个步骤如图5.4所示。


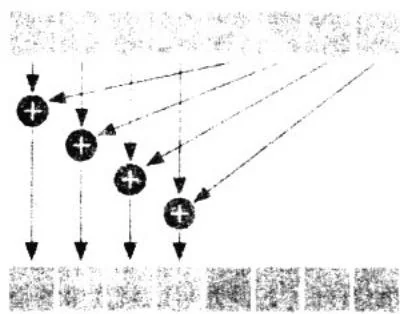
图5.4 求和归约运算中的一个步骤

在完成了一个步骤后，将出现在计算完两两元素乘积后相同的问题。在读取cache[]中的值之前，首先需要确保每个写入cache[]的线程都已经执行完毕。因此，在赋值运算后面增加了__syncthreads调用以确保满足这个条件。

在结束了while()循环后，每个线程块都得到了一个值。这个值位于cache[]的第一个元素中，并且就等于该线程块中两两元素乘积的加和。然后，我们将这个值保存到全局内存并结束核函数：

if (cacheIndex == 0)  
    c[blockIdx.x] = cache[0];

为什么只有cacheIndex==0的线程执行这个保存操作？这是因为只有一个值写入到全局内存，因此只需要一个线程来执行这个操作。当然，每个线程都可以执行这个写入操作，但这么做将使得在写入单个值时带来不必要的内存通信量。为了简单，我们选择了索引为0的线程，当然你也可以选择任何一个线程将cache[0]写入到全局内存。最后，由于每个线程块都只写入一个值到全局数据c[]中，因此可以通过blockIdx来索引这个值。

我们得到了一个数组c[]，其中该数组的每个元素中都包含了某个线程块计算得到的加和值。

点积运算的最后一个步骤就是计算c[]中所有元素的总和。此时，尽管点积运算还没有完全计算完毕，但我们却退出核函数并将执行控制返回到主机。那么，为什么要在尚未计算完成之前就返回到主机？

我们在前面将点积运算称为一种归约运算。大体来说，这是因为最终生成的输出数据数量要小于输入数据的数量。在点积运算中，无论输入的数量有多少，通常只会生成一个输出结果。事实证明，像GPU这种大规模的并行机器在执行最后的归约步骤时，通常会浪费计算资源，因为此时的数据集往往非常小。例如，当使用480个数学处理单元将32个数值相加时，将难以充分使用每一个数学处理单元。

因此，我们将执行控制返回给主机，并且由CPU来完成最后一个加法步骤，即将计算数组c[]中所有元素的总和。如果在一个更大的应用程序中，此时的GPU就可以开始执行其他的点积运算或者其他的大规模计算。然而，在这个示例中，对GPU的使用将到此为止。

在分析这个示例时，我们改变了之前的讲解方式，直接从核函数计算开始分析。接下来将给出main()函数及其对核函数的调用，这与我们在前面给出的代码非常相似。

const int blocksPerGrid =  
    imin(32, (N+threadsPerBlock-1) / threadsPerBlock  
int main(void) {  
    float *a, *b, c, *partial_c;  
    float *dev_a, *dev_b, *dev_partial_c;  
    // 在CPU上分配内存  
    a = new float[N];  
    b = new float[N];  
    partial_c = new float[blocksPerGrid];  
    // 在GPU上分配内存  
    HANDLE_ERROR(cudaMalloc((void**)&dev_a, N*sizeof(float)));  
    HANDLE_ERROR(cudaMalloc((void**)&dev_b, N*sizeof(float)));  
    HANDLE_ERROR(cudaMalloc((void**)&dev_partial_c, blocksPerGrid*sizeof(float)));  
    // 填充主机内存  
    for (int i=0; i<N; i++) {  
        a[i] = i;  
        b[i] = i*2;  
    }
// 将数组 'a' 和 'b' 复制到GPU上  
HANDLE_ERROR(udaMemcpy(dev_a, a, N*size(float),udaMemcpyHostToDevice());  
HANDLE_ERROR(udaMemcpy(dev_b, b, N*size(float),udaMemcpyHostToDevice());  
dot<<<blocksPerGrid, threadsPerBlock>>(dev_a,dev_b,dev_partial_c);

我们来简单总结一下这段代码：

1）为输入数组和输出数组分配主机内存和设备内存。
2）填充输入数组a[]和b[]，然后通过CUDAMemcpy()将它们复制到设备上。
3）在调用计算点积的核函数时指定线程格中线程块的数量以及每个线程块中的线程数量。

尽管大部分代码对你来说已经很熟悉了，但线程块数量的计算过程还值得进一步分析。我们介绍了点积运算是一种归约运算，以及每个线程块如何计算临时和值。对于CPU来说，虽然这段求和的代码非常短，但却足以生成足够多的线程块使GPU始终处于忙碌状态。我们选择了32个线程块，选择其他的值可能会产生更好或者更差的性能，这要取决于CPU和GPU的相对速度。

然而，对于一段非常短的代码选择32个线程块并且每个线程块包含256个线程，那么是否会造成线程过多的情况？如果有N个数据元素，那么通常只需要N个线程来计算点积。但在这里的情况中，线程数量应该为threadsPerBlock的最小整数倍，并且要大于或者等于N。在前面的矢量加法示例中遇到过这种情况。在这里采用的计算公式为 (N+(threadsPerBlock−1))/threadsPerBlock(\mathrm{N} + (\mathrm{threadsPerBlock - 1})) / \mathrm{threadsPerBlock} 。你可能会说，这实际上是整数运算中一种很常见的方法，因此即使你的大部分时间都是放在与CUDA C相关的问题上，但仍然需要理解这种方法。

因此，我们启动的线程块的数量或者是32个，或者是 (N+(threadsPerBlock−1))/(\mathbf{N} + (\mathrm{threadsPerBlock - 1})) / threadsPerBlock，选择二者中较小的。

const int blocksPerGrid =  
    imin(32, (N+threadsPerBlock-1) / threadsPerBlock);

现在，你应该很清楚main()中的代码了。在核函数执行完毕后，仍然需要通过求和操作计算出结果。但正如在启动核函数之前将输入数组复制到GPU一样，我们需要将输出数组从GPU复制回CPU，然后再对其进行计算。因此，在核函数执行完毕后，我们将保存临时和值的数组复制回来，并在CPU上完成最终的求和运算。

// 将数组 'c' 从GPU复制回CPU  
HANDLE_ERROR(udaMemcpy(partial_c, dev_partial_c,
blocksPerGrid*sizeof(float), CUDAMemcpyDeviceToHost）); //在CPU上完成最终的求和运算   
 $\mathbf{c} = \mathbf{0}$  ·   
for（int  $\mathrm{i} = 0$  ；i<blocksPerGrid;  $\mathrm{i + + }$  ）{ c  $+ =$  partial_c[i];   
1

最后，我们检查是否得到了正确的结果，并释放了在CPU和GPU上分配的内存。检查结果的过程很容易，因为我们有规律地将数据填充进输入数组，其中a[]中的值是从0到N-1的整数，而b[]则是 2∗a[2^{*}a[ 。

//填充主机内存  
for (int i=0; i<N; i++) {  
    a[i] = i;  
    b[i] = i*2;  
}

点积计算结果应该是从0到N-1中每个数值的平方再乘以2。对于喜欢离散数学的读者来说，求解这个求和问题的闭合形式解（Closed-Form Solution）是一个有意思的消遣活动。对于那些缺乏耐心或者不感兴趣的读者，我们在下面直接给出了闭合形式解，以及main()函数的剩余部分。

define sum_squares(x)  $(x^{*}(x + 1)^{*}(2^{*}x + 1) / 6)$  printf(“Does GPU value  $8.6g = 8.6g?\backslash n$  ，c,2\*sum_squares(float)(N-1))）;  
//释放GPU上的内存  
CUDAFree(dev_a);  
CUDAFree(dev_b);  
CUDAFree(dev_partial_c);  
//释放CPU上的内存  
delete[]a;  
delete[]b;  
delete[]partial_c;

下面给出了完整的源代码清单：

include"../common/book.h" #defineimin(a,b）(a<b?a:b) constint  $\mathbf{N} = 33^{*}1024$
const int threadsPerBlock = 256;  
const int blocksPerGrid = imin(32, (N+threadsPerBlock-1) / threadsPerBlock);  
__global__ void dot(float *a, float *b, float *c) {  
    __shared__ float cache[threadsPerBlock];  
    int tid = threadIdx.x + blockIdx.x * blockDim.x;  
    int cacheIndex = threadIdx.x;  
    float temp = 0;  
    while (tid < N) {  
        temp += a[tid] * b[tid];  
        tid += blockDim.x * gridDim.x;  
    }  
//设置cache中相应位置上的值  
cache[cacheIndex] = temp;  
//对线程块中的线程进行同步  
__syncthreads();  
//对于归约运算来说，以下代码要求threadPerBlock必须是2的指数  
int i = blockDim.x/2;  
while (i != 0) {  
    if (cacheIndex < i)  
        cache[cacheIndex] += cache[cacheIndex + i];  
    __syncthreads();  
    i /= 2;  
}  
if (cacheIndex == 0)  
    c[blockIdx.x] = cache[0];  
}  
int main(void) {  
    float *a, *b, c, *partial_c;  
    float *dev_a, *dev_b, *dev_partial_c;  
//在CPU上分配内存  
a = (float*)malloc( N*sizeOf(float));  
b = (float*)malloc( N*sizeOf(float));  
partial_c = (float*)malloc( blocksPerGrid*sizeOf(float));  
//在GPU上分配内存  
HANDLE_ERROR(cudaMalloc( (void**)&dev_a, N*sizeOf(float) ));
HANDLE_ERROR(udaMalloc(void\*\*)&dev_b, N\*sizeof(float)）);   
HANDLE_ERROR(udaMalloc(void\*\*)&dev_partial_c, blocksPerGrid\*sizeof(float））;

//填充主机内存

for (int i=0; i<N; i++) {  
    a[i] = i;  
    b[i] = i*2;  
}

//将数组‘a’和‘b’复制到GPU

HANDLE_ERROR(udaMemcpy( dev_a, a, N*sizeof(float),udaMemcpyHostToDevice));  
HANDLE_ERROR(udaMemcpy( dev_b, b, N*sizeof(float),udaMemcpyHostToDevice));  
dot<<<blocksPerGrid, threadsPerBlock>>>(dev_a, dev_b, dev_partial_c);

//将数组‘c’从GPU复制到CPU

HANDLE_ERROR(udaMemcpy( partial_c, dev_partial_c, blocksPerGrid*sizeof(float),udaMemcpyDeviceToHost));

//在CPU上完成最终的求和运算

c = 0;  
for (int i=0; i<blocksPerGrid; i++) {  
    c += partial_c[i];  
}  
#define sum_squares(x)  $(x^* (x + 1)*(2*x + 1)/6)$   
printf("Does GPU value %.6g = %.6g?\n", c, 2 * sum_squares(float(N - 1)));

// 释放GPU上的内存

CUDAFree( dev_a );   
CUDAFree( dev_b );   
CUDAFree( dev_partial_c );

// 释放CPU上的内存

free(a);   
free(b);   
free(partial_c);

}

5.3.2 （不正确的）点积运算优化

在前面曾简要地介绍了点积运算示例中的第二个__syncthreads()。现在，我们来进一步分析这个函数调用，并尝试对其进行改进。之所以需要第二个__syncthreads()，是因为在循环迭代中更新了共享内存变量cache[]，并且在循环的下一次迭代开始之前，需要确保当前迭代中所有线程的更新操作都已经完成。

int i  $=$  blockDim.x/2;   
while  $(\mathrm{i}! = 0)$  { if (cacheIndex  $<  \mathrm{i})$  cache[cacheIndex]  $+ =$  cache[cacheIndex  $^+$  i]; _syncthreads();  $\mathrm{i} / = 2$  ·

在上面的代码中，我们发现只有当cacheIndex小于i时才需要更新共享内存缓冲区cache[]。由于cacheIndex实际上就等于threadIdx.x，因而这意味着只有一部分的线程会更新共享内存缓存。由于调用__syncthreads的目的只是为了确保这些更新在下一次迭代之前已经完成，因此如果将代码修改为只等待那些需要写入共享内存的线程，是不是就能获得性能提升？我们通过将同步调用移动到if()线程块中来实现这个想法：

int i  $=$  blockDim.x/2;   
while  $(\mathrm{i} != 0)$  { if (cacheIndex  $<  \mathrm{i})$  { cache[cacheIndex]  $+ =$  cache[cacheIndex+i]; _syncthreads(); } i  $= 2$  .

虽然这种优化代码的初衷不错，但却不起作用。事实上，这种情况比优化之前的情况还要糟糕。在对核函数进行修改后，GPU将停止响应，而你也不得不强行终止程序。但为什么这个看似无害的修改会导致如此灾难性的错误。

要回答这个问题，我们可以这样想象：线程块中的每个线程依次通过代码，每次一行。每个线程都执行相同的指令，但对不同的数据进行运算。然而，当每个线程执行的指令位于一个条件语句中，例如if()，那么将出现什么情况。显然，并不是每个线程都会执行这个指令，对不对？例如，考虑一个包含以下代码段的核函数，这段代码试图让奇数索引的线程更新某个变量的值：

int myVar = 0;  
if( threadIdx.x % 2)  
    myVar = threadIdx.x;

在前一个示例中，当线程到达粗体的代码行时，只有奇数索引的线程才会执行它，因为偶数索引的线程将无法满足条件if threadIdx.x % 2)。当奇数索引的线程执行这条指令时，偶数索引的线程就不会执行任何操作。当某些线程需要执行一条指令，而其他线程不需要执行时，这种情况就称为线程发散（Thread Divergence）。在正常的环境中，发散的分支只会使得某些线程处于空闲状态，而其他线程将执行分支中的代码。

但在__syncthreads()情况中，线程发散造成的结果有些糟糕。CUDA架构将确保，除非线程块中的每个线程都执行了__syncthreads()，否则没有任何线程能执行__syncthreads()之后的指令。遗憾的是，如果__syncthreads()位于发散分支中，那么一些线程将永远都无法执行__syncthreads()。因此，由于要确保在每个线程执行完__syncthreads()后才能执行后面的语句，因此硬件将使这些线程保持等待。一直等，一直等，永久地等待下去。

因此，如果在点积运算示例中将__syncthreads()调用移入if()线程块中，那么任何cacheIndex大于或等于i的线程将永远都不能执行__syncthreads()。这将使处理器挂起，因为GPU在等待某个永远都不会发生的事件。

if (cacheIndex < i) {
    cache[cacheIndex] += cache[cacheIndex + i];
    __syncthreads();
}

上述内容是为了说明，虽然__syncthreads()是一种强大的机制，它能确保大规模并行应用程序计算出正确的结果，但由于可能会出现意想不到的结果，我们在使用它时仍然要小心谨慎。

5.3.3 基于共享内存的位图

我们已经看到了可以使用共享内存和__syncthreads来确保数据在继续进行之前就已经就绪。为了提高执行速度，你可能会冒险去掉对__syncthreads()的调用。现在我们就来看一个只有使用__syncthreads()才能保证正确性的图形示例。我们将给出预计的输出结果，以及在没有__syncthreads()时的输出结果。事实证明，错误的结果将是不漂亮的。

main()函数与基于GPU的Julia集示例类似，不过这一次我们在每个线程块中启动多个线程：

include“cuda.h" #include“../common/book.h" #include“../common/cpuBITmap.h" #define DIM 1024 #define PI 3.1415926535897932f int main(void）{
CPUBitmap bitmap(DIM, DIM); unsigned char \*dev_bitmap;   
HANDLE_ERROR(udaMalloc(void\*\&) & dev_bitmap, bitmap(image_size()));   
dim3 grids(DIM/16,DIM/16);   
dim3 threads(16,16);   
kernel<<<grids,threads>>>(dev_bitmap);   
HANDLE_ERROR(udaMemcpy bitmap.get_ptr(),dev_bitmap, bitmap(image_size(),udaMemcpyDeviceToHost))； bitmap.display_and_exit();   
CUDAFree( dev_bitmap );   
}

与Julia集示例一样，每个线程都将为一个输出位置计算像素值。每个线程要做的第一件事情就是计算输出影像中相应的位置x和y。这种计算类似于矢量加法示例中对tid的计算，只是这次计算的是一个二维空间。

__global__ void kernel(unsigned char *ptr) {
    // 将threadIdx/BlockIdx映射到像素位置
    int x = threadIdx.x + blockIdx.x * blockDim.x;
    int y = threadIdx.y + blockIdx.y * blockDim.y;
    int offset = x + y * blockDim.x * gridDim.x;

由于将使用一个共享内存缓冲区来保存计算结果，我们声明了一个缓冲区，在 16×1616 \times 16 的线程块中的每个线程在该缓冲区中都有一个对应的位置。

shared float shared[16][16];

然后，每个线程都会计算出一个值，并将其保存到缓冲区中。

// 现在计算这个位置上的值  
const float period = 128.0f;  
shared(threadIdx.x][threadIdx.y] = 255 * (sinf(x*2.0f*PI/period) + 1.0f) * (sinf(y*2.0f*PI/period) + 1.0f) / 4.0f;
最后，我们将把这些值保存回像素，保留x和y的次序：ptr[offset*4 + 0] = 0;ptr[offset*4 + 1] = shared[15-threadIdx.x][15-threadIdx.y];ptr[offset*4 + 2] = 0;
ptr[offset*4 + 3] = 255;

当然，这些计算有些随意，我们只是绘制了一个由多个绿色球形构成的网格。在编译并运行这个核函数后，将输出图5.5中的图像。


图5.5 在不正确同步情况下得到的截屏

这里发生了什么问题？从我们设计这个示例的初衷，你可能已经猜到了原因，在代码中忽略了一个重要的同步点。当线程将shared[][]中的计算结果保存到像素中时，负责写入到shared[][]的线程可能还没有完成写入操作。确保这种问题不会出现的唯一方法就是使用__synchreads()。没有使用__synchreads()的结果就是得到一张被破坏的图片，充满了绿色的球形。

虽然在这个程序中并没有造成严重后果，但如果应用程序的计算非常重要，那么造成的破坏将是巨大的。

要解决这个问题，我们需要在写入共享内存与读取共享内存之间添加一个同步点。

shared[threadIdx.x][threadIdx.y] = 255 * (sinf(x*2.0f*PI/ period) + 1.0f) * (sinf(y*2.0f*PI/ period) + 1.0f) / 4.0f;  
__syncthreads();  
ptr[offset*4 + 0] = 0;
ptr[offset*4 + 1] = shared[15-threadIdx.x][15-threadIdx.y];  
ptr[offset*4 + 2] = 0;  
ptr[offset*4 + 3] = 255;

在添加__syncthreads()调用后，我们就可以获得一个预期的结果（并且从审美的角度来看也是更漂亮的），如图5.6所示。


图5.6 在添加了正确同步之后的截屏

前の章5.2_并行线程块的分解
次の章5.4_本章小结
5.3_共享内存和同步 - CUDA by Example | OpenTech