5.2_并行线程块的分解
5.2 并行线程块的分解
在第4章中,我们看到了如何在GPU上启动并行代码。具体的实现方法是,告诉CUDA运行时启动核函数的多个并行副本。我们将这些并行副本称为线程块(Block)。
CUDA运行时将把这些线程块分解为多个线程。当需要启动多个并行线程块时,只需将尖括号中的第一个参数由1改为想要启动的线程块数量。例如,在介绍矢量加法示例时,我们为矢量中的每个元素(共有N个元素)都启动了一个线程块,如下所示:
在尖括号中,第二个参数表示CUDA运行时在每个线程块中创建的线程数量。上面这行代码表示在每个线程块中只启动一个线程。总共启动的线程数量可按以下公式计算:
事实上,我们也可以启动N/2个线程块,每个线程块包含2个线程,或者N/4个线程块,每个线程块包含4个线程,以此类推。接下来,我们将围绕着CUDA C的这种特性来重新回顾矢量相加示例。
5.2.1 矢量求和:重新回顾
在本节中将完成与第4章中相同的任务,即将两个输入矢量相加并将结果保存在第三个输出矢量中。然而,这一次我们将使用线程而不是线程块来实现。
你可能会奇怪,使用线程与使用线程块相比存在哪些优势?就目前而言,几乎没有任何优势。但线程块中的并行线程能够完成并行线程块无法完成的工作。因此,在分析接下来基于并行线程的矢量求和程序时,要保持耐心。
1. 使用线程实现GPU上的矢量求和
在将实现方式由并行线程块改为并行线程时,首先需要修改两个地方。第一个地方是,之前核函数的调用中是启动N个线程块,并且每个线程块对应一个线程,如下所示:
add<<N,1>>>(dev_a,dev_b,dev_c);现在,我们将启动N个线程,并且所有线程都在一个线程块中:
add<<1,N>>>(dev_a,dev_b,dev_c);第二个要修改的地方是对数据进行索引的方法。之前核函数中是通过线程块索引对输入数据和输出数据进行索引。
int tid = blockIdx.x;你应该对上面这行代码很熟悉了。现在,由于只有一个线程块,因此需要通过线程索引来对数据进行索引。
int tid = threadIdx.x;这就是将使用并行线程块修改为使用并行线程时需要进行的两处修改。下面给出了完整的源代码,其中有变化的代码行用粗体显示:
include"../common/book.h"
#define N 10
.globalvoid add(int \*a,int \*b,int \*c){ int tid $=$ threadIdx.x; if(tid $< \mathbf{N}$ ) c[tid] $= a$ [tid] $^+$ b[tid];
}
int main(void){ int a[N],b[N],c[N]; int \*dev_a,\*dev_b,\*dev_c; //在GPU上分配内存
HANDLE_ERROR(udaMalloc( (void\*\*)&dev_a,N\*sizeof(int)));
HANDLE_ERROR(udaMalloc( (void\*\*)&dev_b,N\*sizeof(int)));
HANDLE_ERROR(udaMalloc( (void\*\*)&dev_c,N\*sizeof(int)));
//在CPU上为数组‘a’和‘b’赋值 for(int $\mathrm{i = 0}$ :i<N;i++) { a[i] $= i$ · $\textit{\textbf{b}} [\textit{i}] = \textit{\textbf{i}} *\textit{\textbf{i}}$ 1
//将数组‘a’和‘b’复制到GPU
HANDLE_ERROR(udaMemcpy(dev_a,N\*sizeof(int),udaMemcpyHostToDevice));
HANDLE_ERROR(udaMemcpy( dev_b,b,N\*sizeof(int),udaMemcpyHostToDevice));
add<<1,N>>>(dev_a,dev_b,dev_c);
//将数组‘c’从GPU复制到CPU
HANDLE_ERROR(udaMemcpy( c,dev_c,N\*sizeof(int),udaMemcpyDeviceToHost));
//显示结果
for(int $\mathrm{i} = 0$ :i<N;i++){printf(“d+ $\text{色}$ d= $\text{色}$ d\n”,a[i],b[i],c[i]);
}
//释放在GPU上分配的内存
CUDAFree( dev_a);
CUDAFree( dev_b);
CUDAFree( dev_c);
return 0;这段代码非常简单,对不对?在下一节中,我们将看到在这种只使用并行线程的方法中存在的局限。此外,我们还将看到为什么要将线程块分解为其他的并行部分。
2. 在GPU上对更长的矢量求和
在第4章中,我们注意到硬件将线程块的数量限制为不超过65535。同样,对于启动核函数时每个线程块中的线程数量,硬件也进行了限制。具体来说,最大的线程数量不能超过设备属性结构中maxThreadsPerBlock域的值,我们在第3章中介绍过这个结构。对于当前的许多图形处理器而言,这个限制值是每个线程块512个线程。因此,如何通过并行线程对长度大于512的矢量进行相加?在这种情况下,我们必须将线程与线程块结合起来才能实现这个计算。
与前面一样,这里需要改动两个地方:核函数中的索引计算方法和核函数的调用方式。
现在,我们需要多个线程块并且每个线程块中包含了多个线程,计算索引的方法看上去非常类似于将二维索引空间转换为线性空间的标准算法。
int tid = threadIdx.x + blockIdx.x * blockDim.x;在上面的赋值语句中使用了一个新的内置变量,blockDim。对于所有线程块来说,这个变量是一个常数,保存的是线程块中每一维的线程数量。由于使用的是一维线程块,因此只需用到blockDim.x。回顾第4章的内容,在gridDim中保存了一个类似的值,即在线程格中每一维的线程块数量。此外,gridDim是二维的,而blockDim实际上是三维的。也就是说,CUDA运行时允许启动一个二维线程格,并且线程格中的每个线程块都是一个三维的线程数组。没错,这是一种高维数组,虽然你很少会用到这种高维索引,但如果需要也可以支持。
通过前面的运算来对线性数组中的数据进行索引是非常直观的。它可以帮助你从空间上来思考线程集合,这类似于一个二维的像素数组。在图5.1中给出了这种空间组织形式。
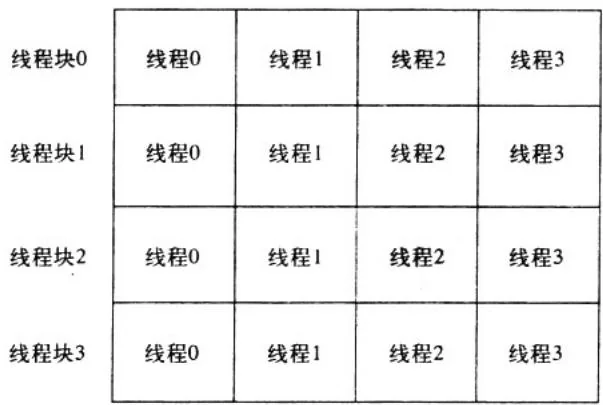
图5.1 线程块集合与线程集合的二维组织形式
如果线程表示列,而线程块表示行,那么可以计算得到一个唯一的索引:将线程块索引与每个线程块中的线程数量相乘,然后加上线程在线程块中的索引。这与我们在Julia集中将二维图像索引线性化的方法是相同的。
在这里,DIM表示线程块的大小(即线程的数量),y为线程块索引,并且x为线程块中的线程索引。因此可以计算得到以下索引:tid = threadIdx.x + blockIdx.x * blockDim.x。
另一处修改是核函数调用本身。虽然仍需要启动N个并行线程,但我们希望在多个线程块中启动它们,这样就不会超过512个线程的最大数量限制。其中一种解决方案是,将线程块的大小设置为某个固定数值,在这个示例中,我们每个线程块中包含的线程数量固定为128。然后,可以启动N/128个线程块,这样总共就启动了N个线程同时运行。
这里的问题在于,N/128是一个整数除法。例如,如果N为127,那么N/128等于0,因此将启动0个线程,而我们实际上也不会获得任何计算结果。事实上,当N不是128的整数倍时,启动的线程数量将少于预期数量,这种情况非常糟糕。事实上,我们希望这个除法能够向上取整。
我们可以通过一种常见的技术在整数除法中实现这个功能。不是调用ceil(),而是计算(N+127)/128而不是N/128。你也可以将这种算法理解为,计算大于或等于N的128的最小倍数。
我们选择了每个线程块拥有128个线程,因此使用以下的核函数调用:
add<< $(N + 127) / 128$ , $128 \ggg$ (dev_a, dev_b, dev_c);上面这行代码对除法进行了修改从而确保启动足够多的线程,因此当N不是128个整数倍时,将启动过多的线程。然而,在核函数中已经解决了这个问题。在访问输入数组和输出数组之前,必须检查线程的偏移是否位于0到N之间。
if (tid < N)
c[tid] = a[tid] + b[tid];因此,当索引越过数组的边界时,例如当启动的并行线程数量不是128的整数倍时就会出现这种情况,那么核函数将自动停止执行计算。更重要的是,核函数不会对越过数组边界的内存进行读取或者写入。
3. 在GPU上对任意长度的矢量求和
当第一次介绍在GPU上启动并行线程块时,我们并没有考虑所有可能的情况。除了在线程数量上存在限制外,在线程块的数量上同样存在着一个硬件限制(虽然这个限制值比线程数量的限制值更大)。在前面提到过,线程格每一维的大小都不能超过65535。
因此,这就对矢量加法的实现带来了一个问题。如果启动N/128个线程块将矢量相加,那么当矢量的长度超过 时,核函数调用会失败。这看上去似乎是一个很大的数值,但在当前内存容量基本上在1GB到4GB的情况下,高端图形处理器能够容纳元素数量超过8百万的矢量。
幸运的是,这个问题的解决方案非常简单。我们首先对核函数进行一些修改。
__global__ void add(int *a, int *b, int *c) {
int tid = threadIdx.x + blockIdx.x * blockDim.x;
while (tid < N) {
c[tid] = a[tid] + b[tid];
tid += blockDim.x * gridDim.x;
}
}这看上去非常像矢量加法的最初版本。我们将它与第4章中基于CPU的实现进行比较:
void add(int *a, int *b, int *c) {
int tid =; //这是第0号CPU,因此索引从0开始
while (tid < N) {
c[tid] = a[tid] + b[tid];tid $+ = 1$ //由于只有一个CPU,因此每次递增1}在这里,我们使用了一个while()循环对数据进行迭代。之前提到过,在多CPU或者多核版本中,每次递增的数量不是1,而是CPU的数量。现在,我们在GPU版本中将使用同样的方法。
在GPU实现中,我们将并行线程的数量看成是处理器的数量。尽管GPU的处理单元数量可能小于(或者大于)这个值,但我们认为每个线程在逻辑上都可以并行执行,并且硬件可以调度这些线程以便实际执行。通过将并行化过程与硬件的实际执行过程解耦开来,这是CUDA C为软件开发人员减轻的负担之一。这种解耦起到了极大的帮助作用,特别是考虑到当前NVIDIA硬件在每个芯片上可能包含了从8个到480个的数学单元!
在理解了上述实现方式所包含的核心思想后,我们只需知道如何计算每个并行线程的初始索引,以及如何确定递增的量值。我们希望每个并行线程从不同的索引开始,因此就需要对线程索引和线程块索引进行线性化,正如在5.2.1节中看到的。每个线程的起始索引按照以下公式来计算:
int tid = threadIdx.x + blockIdx.x * blockDim.x;在每个线程计算完当前索引上的任务后,接着就需要对索引进行递增,其中递增的步长为线程格中正在运行的线程数量。这个数值等于每个线程块中的线程数量乘以线程格中线程块的数量,即 。因此,递增语句如下所示:
tid $+ =$ blockDim.x \* gridDim.x;我们几乎要完成了!剩下的事情就是修改核函数调用本身。前面提到过,之所以采用这种方式,是因为当 大于65535时,核函数调用add (dev_a,dev_b.dev_c)会失败。为了确保不会启动过多的线程块,我们将线程块的数量固定为某个较小的值。由于我们非常喜欢直接复制和粘贴代码,因此在这里同样使用128个线程块,并且每个线程块包含128个线程。
add<<128,128>>>(dev_a,dev_b,dev_c);你也可以将这些值调整为你认为合适的任意值,只要你指定的值仍处于前面给出的限制范围之内。在本书的后面部分,我们将讨论不同的值对性能产生的影响,但就目前来说,选择128个线程块并且每个线程块包含128个线程就足够了。现在,我们将把任意长度的矢量相加起来,矢量长度的限制只取决于GPU上的内存容量。以下是完整的源代码清单:
include"../common/book.h"
#defineN(33\*1024) _globalvoidadd(int \*a,int \*b,int \*c){int tid $=$ threadIdx.x $^+$ blockIdx.x \* blockDim.x; while (tid $< \mathbb{N}$ ){ c[tid] $= \mathrm{a}[\mathrm{tid}] + \mathrm{b}[\mathrm{tid}]$ ; tid $+ =$ blockDim.x \* gridDim.x; }
}
int main(void){ int a[N], b[N], c[N]; int \*dev_a, \*dev_b, \*dev_c; //在GPU上分配内存 HANDLE_ERROR(udaMalloc((void\*\*)&dev_a,N\*sizeof(int))); HANDLE_ERROR(udaMalloc((void\*\*)&dev_b,N\*sizeof(int))); HANDLE_ERROR(udaMalloc((void\*\*)&dev_c,N\*sizeof(int))); //在CPU上为数组‘a’和‘b’赋值 for(int i=0;i<N;i++) { a[i] $= \mathrm{i}$ . b[i] $= \mathrm{i}\ast \mathrm{i}$ ·
1 //将数组‘a’和‘b’复制到GPU HANDLE_ERROR(udaMemcpy( dev_a, a, N\*sizeof(int),udaMemcpyHostToDevice)); HANDLE_ERROR(udaMemcpy( dev_b, b, N\*sizeof(int),udaMemcpyHostToDevice)); add<<128,128>>>(dev_a,dev_b,dev_c); //将数组‘c’从GPU复制到CPU HANDLE_ERROR(udaMemcpy( c, dev_c, N\*sizeof(int),udaMemcpyDeviceToHost)); //验证GPU确实完成了我们要求的工作 bool success $=$ true; for(int i=0;i<N;i++){ if((a[i] $^+$ b[i])! $= \mathrm{c}[i]$ ){ printf("Error:%d+%d != %d\n",a[i],b[i],c[i]); success $=$ false;}
} if (success) printf( "We did it1\n"); //释放在GPU上分配的内存
CUDAFree( dev_a);
CUDAFree( dev_b);
CUDAFree( dev_c);
return 0;
}5.2.2 在GPU上使用线程实现波纹效果
在第4章中,我们通过一个有趣的示例来说明已经学习到的各项技术。在本章中,我们同样将通过GPU的强大计算能力来生成一些图片。为了实现更有趣的演示效果,这一次我们将实现动画显示。当然,我们将把所有不相关的动画代码都封装到辅助函数中,这样你就无需预先掌握任何图形技术或者动画技术。
struct DataBlock{ unsigned char \*dev bitmap; CPUAnimBitmap \* bitmap;
};
//释放在GPU上分配的内存
void cleanup(DataBlock \*d){ CUDAFree(d->dev bitmap);
}
int main(void){ DataBlock data; CPUAnimBitmap bitmap(DIM,DIM,&data); data.bitmap $=$ &bitmap; HANDLE_ERROR( CUDAAlloc( (void\*\*)&data.dev bitmap, bitmap(image_size())); bitmap.anim_and_exit( (void $(^{*})$ (void\*,int))generate_frame, (void $(^{*})$ (void\*))cleanup);
}main()函数的大部分复杂性都被隐藏在辅助类CPUAnimBitmap中。你将注意到,我们再次遵循了前面采用的模式,即首先调用CUDAAlloc(),然后执行设备代码对内存内容进行计算,最后调用CUDAFree()来释放这些内存。这些步骤对你来说应该已经很熟悉了。
在这个示例中,我们将把“执行设备代码对内存内容进行计算”这个步骤变得更复杂一些。我们将一个指向generate_frame()的函数指针传递给anim_and_exit()。每当要生成一帧新的动画时,都将调用函数generate_frame()。
void generate_frame(DataBlock \*d,int ticks){ dim3 blocks(DIM/16,DIM/16); dim3 threads(16,16); kernel<<<blocks,threads>>>(d->dev bitmap,ticks); HANDLE_ERROR(cudaMemcpy(d-> bitmap->get_ptr(), d->dev bitmap, d-> bitmap->image_size(), CUDAMemcpyDeviceToHost));
}尽管这个函数只包含了4行代码,但其中却包含CUDA C的所有重要概念。首先,代码声明了两个二维变量,blocks和threads。从名字就可以很清楚地看到,变量blocks表示在线程格中包含的并行线程块数量。变量threads表示在每个线程块中包含的线程数量。由于生成的是一幅图像,因此使用了二维索引,并且每个线程都有一个唯一的索引 ,这样可以很容易与输出图像中的像素一一对应起来。在我们选择的线程块中包含了一个大小为 的线程数组。如果图像有DIM×DIM个像素,那么就需要启动DIM/16×DIM/16个线程块,从而使每个像素对应一个线程。在图5.2中给出了在一个(非常小的)48像素宽和32像素高的图像中的线程块与线程的配置情况。
如果你曾经编写过多线程的CPU程序,那么可能会奇怪为什么要启动这么多的线程。例如,如果绘制一个 的动画,那么这种方法将创建超过2百万个线程。虽然我们可以在GPU上创建和调度这么多的线程,但任何人都难以想象在CPU上创建这么多的线程。由于CPU的线程管理和调度必须在软件中完成,因此无法像GPU那样能支持数量如此多的线程。由于我们为每个需要处理的元素都创建了一个线程,因此在GPU上的并行编程就比在CPU上要简单得多。
在声明了表示线程块数量和线程数量的变量后,接下来就需要调用核函数来计算像素值。
kernel<< blocks, threads>>>(d->dev bitmap, ticks);核函数需要包含两个参数。首先,它需要一个指针来指向保存输出像素值的设备内存。这是一个全局变量,它指向的内存是在main()中分配的。然而,这个变量只是对于主机代码来说是“全局的”,因此我们需要将其作为一个参数传递进去,从而确保设备代码能够访问这个变量。
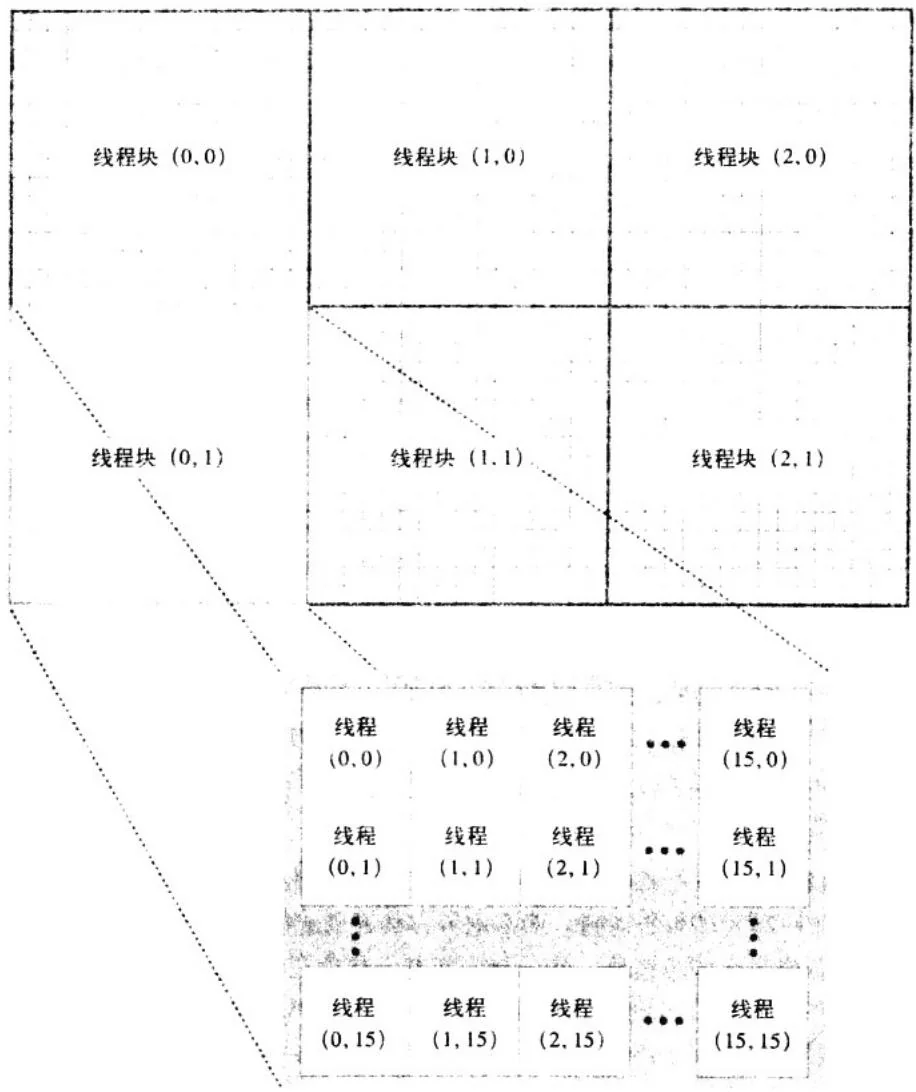
图5.2 线程块与线程的二维层次结构图,用于处理一个 像素的图像,其中每个像素对应一个线程
其次,核函数需要知道当前的动画时间以便生成正确的帧。在CPUAnimBitmap的代码中将当前时间 ticks 传递给 generate_frame(),因此只需直接将这个值传递给核函数。
核函数的代码如下所示:
.global__void kernel(unsigned char *ptr, int ticks) { // 将threadIdx/BlockIdx映射到像素位置
int x = threadIdx.x + blockIdx.x * blockDim.x;
int y = threadIdx.y + blockIdx.y * blockDim.y;
int offset $= \mathrm{x} + \mathrm{y}$ \*blockDim.x \*gridDim.x;
//现在计算这个位置上的值
float fx $= \mathbf{x}$ -DIM/2;
float fy $= y$ -DIM/2;
float d $=$ sqrtf(fx \*fx+fy \*fy);
unsigned char grey $=$ (unsigned char)(128.0f+127.0f\* cos(d/10.0f-ticks/7.0f)/(d/10.0f+1.0f));
ptr[offset\*4+0] $=$ grey;
ptr[offset\*4+1] $=$ grey;
ptr[offset\*4+2] $=$ grey;
ptr[offset\*4+3] $= 255$前三行代码是核函数中最重要的代码。
int x = threadIdx.x + blockIdx.x * blockDim.x;
int y = threadIdx.y + blockIdx.y * blockDim.y;
int offset = x + y * blockDim.x * gridDim.x;在这几行代码中,每个线程都得到了它在线程块中的索引以及这个线程块在线程格中的索引,并将这两个值转换为图形中的唯一索引 。例如,当位于线程格中(12,8)处的线程块中的(3,5)处的线程开始执行时,它知道在其左边有12个线程块,而在它上边有8个线程块。在这个线程块内,(3,5)处线程的左边有3个线程,并且在它上边有5个线程。由于每个线程块都有16个线程,这就意味着这个线程有:
3线程 线程块 线程/线程块 个线程在其左边
5线程 线程块 线程/线程块 个线程在其上边
这个计算就是计算前两行中的x和y,也是将线程和线程块的索引映射到图像坐标的算法。然后,我们对x和y的值进行线性化从而得到输出缓冲区中的一个偏移。这与5.2.1节的第2个标题以及第3个标题中的工作是相同的。
int offset = x + y * blockDim.x * gridDim.x;既然我们知道了线程要计算的像素值 ,以及在何时计算这个值,那么就可以计算 的任意函数,并将这个值保存在输出缓冲区中。在这里的情况中,函数将生成一个随时间变化的正弦曲线“波纹”。
float $\mathrm{f}\mathbf{x} = \mathbf{x} - \mathrm{DIM} / 2$
float $\mathrm{fy} = \mathrm{y} - \mathrm{DIM} / 2$
floatd $=$ sqrtf(fx\*fx+fy\*fy);
unsigned char grey $=$ (unsigned char)(128.0f + 127.0f我们建议你不要花太多的时间去理解grey值的计算。这其实只是一个2维时间函数,当动画显示时,将会形成一个漂亮的波纹效果。其中一帧的截屏如图5.3所示。

图5.3 GPU波纹示例的截图