0x43线段树

线段树（SegmentTree）是一种基于分治思想的二叉树结构，用于在区间上进行信息统计。与按照二进制位（2 的次幂）进行区间划分的树状数组相比，线段树是一种更加通用的结构：

线段树的每个节点都代表一个区间。
线段树具有唯一的根节点，代表的区间是整个统计范围，如 $[1, N]$ 。
线段树的每个叶节点都代表一个长度为 1 的元区间 $[x, x]$ 。
对于每个内部节点 $[l, r]$ ，它的左子节点是 $[l, mid]$ ，右子节点是 $[mid + 1, r]$ ，其中 $mid = (l + r)/2$ （向下取整）。

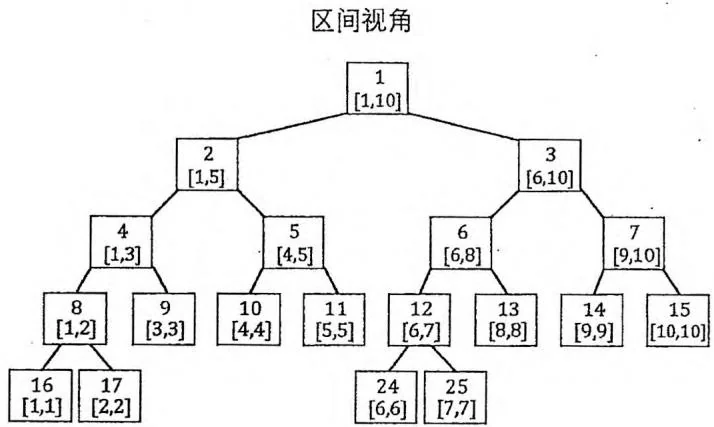
二叉树视角

上图展示了一棵线段树。可以发现，除去树的最后一层，整棵线段树一定是一棵完全二叉树，树的深度为 $O(\log N)$ 。因此，我们可以按照与二叉堆类似的“父子2倍”节点编号方法：

根节点编号为 1。
编号为 $x$ 的节点的左子节点编号为 $x * 2$ ，右子节点编号为 $x * 2 + 1$ 。

这样一来，我们就能简单地使用一个struct数组来保存线段树。当然，树的最后一层节点在数组中保存的位置不是连续的，直接空出数组中多余的位置即可。在理想情况下， $N$ 个叶节点的满二叉树有 $N + N / 2 + N / 4 + \dots + 2 + 1 = 2N - 1$ 个节点。因为在上述存储方式下，最后还有一层产生了空余，所以保存线段树的数组长度要不小于 $4N$ 才能保证不会越界。

线段树的建树

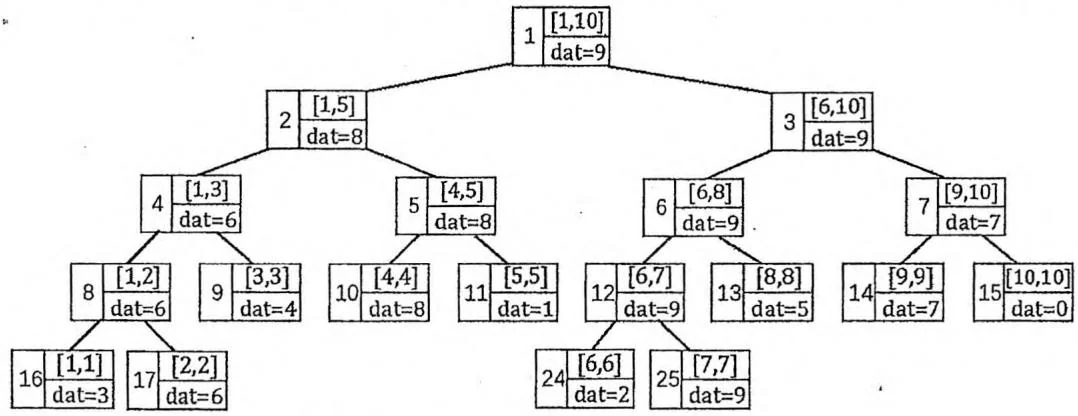
线段树的基本用途是对序列进行维护，支持查询与修改指令。给定一个长度为 $N$ 的序列 $A$ ，我们可以在区间 $[1,N]$ 上建立一棵线段树，每个叶节点 $[i,i]$ 保存 $A[i]$ 的值。线段树的二叉树结构可以很方便地从下往上传递信息。以区间最大值问题为例，记 $\mathrm{dat}(l,r)$ 等于 $\max_{l\leq i\leq r}\{A[i]\}$ ，显然 $\mathrm{dat}(l,r) = \max \bigl (\mathrm{dat}(l,mid),\mathrm{dat}(mid + 1,r)\bigr)$ 。

Build(1,1,10)  $A = \{3,6,4,8,1,2,9,5,7,0\}$

下面这段代码建立了一棵线段树并在每个节点上保存了对应区间的最大值。

struct SegmentTree {
    int l, r;
    int dat;
} t[SIZE * 4]; // struct 数组存储线段树
void build(int p, int l, int r) {
    t[p].l = l, t[p].r = r; // 节点 p 代表区间[l,r]
    if (l == r) { t[p].dat = a[l]; return; } // 叶节点
    int mid = (l + r) / 2; // 折半
    build(p*2, l, mid); // 左子节点[l,mid], 编号 p*2
    build(p*2+1, mid+1, r); // 右子节点[mid+1,r], 编号 p*2+1
    t[p].dat = max(t[p*2].dat, t[p*2+1].dat); // 从下往上传递信息
}

build(1, 1, n); // 调用入口

线段树的单点修改

单点修改是一条形如“C x v”的指令，表示把 $A[x]$ 的值修改为 $v$ 。

在线段树中，根节点（编号为1的节点）是执行各种指令的入口。我们需要从根节点出发，递归找到代表区间 $[x, x]$ 的叶节点，然后从下往上更新 $[x, x]$ 以及它的所有祖先节点上保存的信息，如下图所示。时间复杂度为 $O(\log N)$ 。

void change(int p, int x, int v) {
    if (t[p].l == t[p].r) { t[p].dat = v; return; } // 找到叶节点
    int mid = (t[p].l + t[p].r) / 2;
    if (x <= mid) change(p*2, x, v); // x属于左半区间
    else change(p*2+1, x, v); // x属于右半区间
    t[p].dat = max(t[p*2].dat, t[p*2+1].dat); // 从下往上更新信息
}

change(1, x, v); // 调用入口

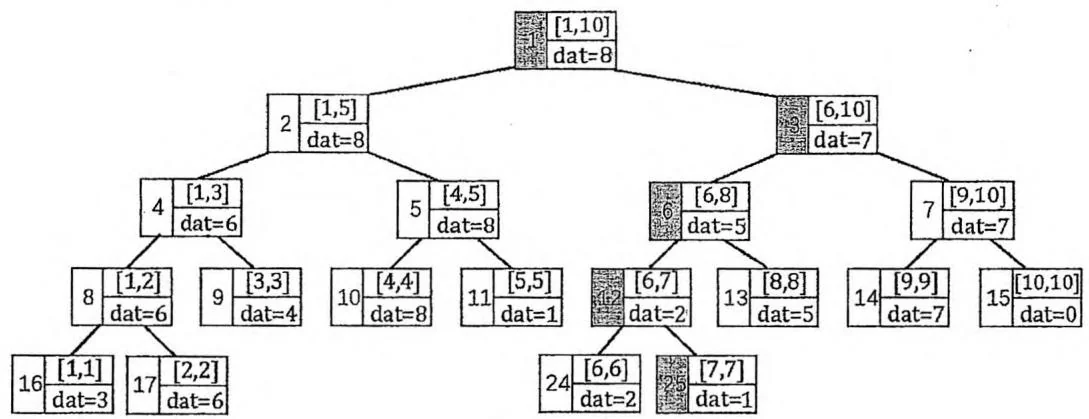
change(1,7,1)

线段树的区间查询

区间查询是一条形如“Q $l$ r”的指令，例如查询序列A在区间 $[l,r]$ 上的最大值，即max $\lim_{l\leq i\leq r}\{A[i]\}$ 。我们只需要从根节点开始，递归执行以下过程：

若 $[l, r]$ 完全覆盖了当前节点代表的区间，则立即回溯，并且该节点的 $dat$ 值为候选答案。
若左子节点与 $[l, r]$ 有重叠部分，则递归访问左子节点。
若右子节点与 $[l, r]$ 有重叠部分，则递归访问右子节点。

int ask(int p, int l, int r) {
    if (l <= t[p].l && r >= t[p].r) return t[p].dat; // 完全包含
    int mid = (t[p].l + t[p].r) / 2;

int val $= -(1 < < 30)$ ;//负无穷大if（1<=mid）val $= \max (\mathrm{val},$ ask(p*2，1，r));//左子节点有重叠if（r>mid）val $= \max (\mathrm{val},$ ask(p*2+1，1，r));//右子节点有重叠return val;

cout << ask(1, 1, r) << endl; // 调用入口

\operatorname {A s k} (1, 2, 8) = \max \{6, 4, 8, 5 \} = 8

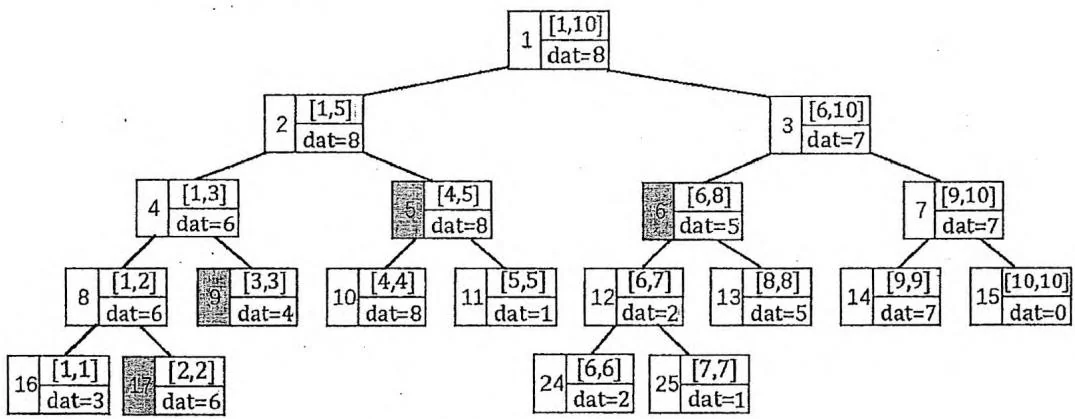
该查询过程会把询问区间 $[l, r]$ 在线段树上分成 $O(\log N)$ 个节点，取它们的最大值作为答案。为什么是 $O(\log N)$ 个呢？仔细分析上述过程，在每个节点 $[p_l, p_r]$ 上，设 $mid = (p_l + p_r)/2$ （向下取整），可能会出现以下几种情况：

$l \leq p_{l} \leq p_{r} \leq r$ ，即完全覆盖了当前节点，直接返回。
$p_l \leq l \leq p_r \leq r$ ，即只有 $l$ 处于节点之内。

(1) $l > m i d$ ，只会递归右子树。
(2) $l \leq m i d$ , 虽然递归两棵子树, 但是右子节点会在递归后直接返回。

$l \leq p_{l} \leq r \leq p_{r}$ , 即只有 $r$ 处于节点之内, 与情况 2 类似。
$p_l \leq l \leq r \leq p_r$ ，即 $l$ 与 $r$ 都位于节点之内。

(1) $l, r$ 都位于 mid 的一侧，只会递归一棵子树。
(2) $l, r$ 分别位于 mid 的两侧，递归左右两棵子树。

也就是说，只有情况4(2)会真正产生对左右两棵子树的递归。请读者思考，这种情况至多发生一次，之后在子节点上就会变成情况2或3。因此，上述查询过程的时间复杂度为 $O(2\log N) = O(\log N)$ 。从宏观上理解，相当于 $l,r$ 两个端点分别在线段树上划分出一条递归访问路径，情况4(2)在两条路径在从下往上的第一次交会处产生。

至此，线段树已经能够像0x06节的ST算法一样处理区间最值问题，并且还支持动态修改某个数的值。同时，线段树也已经能支持上一节中树状数组的单点增加与查询

前缀和指令。在讨论区间修改之前，我们先来通过几道例题加深对线段树的印象。

【例题】Can you answer on these queries III SPOJ GSS3

给定长度为 $N$ 的数列 $A$ ，以及 $M$ 条指令 $(N,M\leq 50000)$ ，每条指令可能是以下两种之一：

“0 x y”, 把 $A[x]$ 改成 $y$ 。
“1xy”，查询区间 $[x,y]$ 中的最大连续子段和，即 $\max_{x\leq l\leq r\leq y}\{\sum_{i = l}^{r}A[i]\}$

对于每个询问，输出一个整数表示答案。

在线段树上的每个节点上，除了区间端点外，再维护4个信息：区间和sum，区间最大连续子段和dat，紧靠左端的最大连续子段和lmax，紧靠右端的最大连续子段和rmax。

线段树的整体框架不变，我们只需完善在 build 和 change 函数中从下往上传递的信息：

\begin{array}{l} t [ p ]. \text {s u m} = t [ p * 2 ]. \text {s u m} + t [ p * 2 + 1 ]. \text {s u m} \\ t [ p ]. \operatorname {l m a x} = \max (t [ p * 2 ]. \operatorname {l m a x}, t [ p * 2 ]. \operatorname {s u m} + t [ p * 2 + 1 ]. \operatorname {l m a x}) \\ t [ p ]. \operatorname {r m a x} = \max (t [ p * 2 + 1 ]. \operatorname {r m a x}, t [ p * 2 + 1 ]. \operatorname {s u m} + t [ p * 2 ]. \operatorname {r m a x}) \\ t [ p ]. \mathrm {d a t} = \max (t [ p * 2 ]. \mathrm {d a t}, t [ p * 2 + 1 ]. \mathrm {d a t}, t [ p * 2 ]. \mathrm {r m a x} + t [ p * 2 + 1 ]. \mathrm {l m a x}) \\ \end{array}

从这道题目我们也可以看出，线段树作为一种比较通用的数据结构，能够维护各式各样的信息，前提是这些信息容易按照区间进行划分与合并（又称满足区间可加性）。我们只需要在父子传递信息和更新答案时稍作变化即可。

【例题】IntervalGCD

给定一个长度为 $N$ 的数列 $A$ ，以及 $M$ 条指令 $(N, M \leq 2 * 10^{5})$ ，每条指令可能是以下两种之一：

“C $l r d$ ”，表示把 $A[l], A[l + 1], \dots, A[r]$ 都加上 $d$ 。
“Q $l$ $r$ ”, 表示询问 $A[l], A[l + 1], \dots, A[r]$ 的最大公约数(GCD)。

对于每个询问，输出一个整数表示答案。

根据“《九章算术》之更相减损术”，我们知道 $\gcd (x,y) = \gcd (x,y - x)$ 。它可以进一步扩展到三个数的情况： $\gcd (x,y,z) = \gcd (x,y - x,z - y)$ 。实际上，读者用数学归纳法容易证明，该性质对任意多个整数都成立。

因此，我们可以构造一个长度为 $N$ 的新数列 $B$ ，其中 $B[i] = A[i] - A[i - 1]$ ， $B[1]$ 可为任意值。数列 $B$ 称为 $A$ 的差分序列。用线段树维护序列 $B$ 的区间最大公约数。

这样一来，询问“Q $l$ r”，就等于求出 $\gcd (A[l],ask(1,l + 1,r))$

在指令“C $l r d$ ”下，只有 $B[l]$ 加了 $d$ ， $B[r + 1]$ 被减掉了 $d$ ，所以在维护 $B$ 的线段树上只需进行两次单点修改即可。另外，询问时需要数列 $A$ 中的值，可额外用一个支持“区间增加、单点查询”的树状数组对数列 $A$ 进行维护。

$\spadesuit$ 延迟标记

在线段树的“区间查询”指令中，每当遇到被询问区间 $[l, r]$ 完全覆盖的节点时，可以立即把该节点上存储的信息作为候选答案返回。我们已经证明，被询问区间 $[l, r]$ 在线段树上会被分成 $O(\log N)$ 个小区间（节点），从而在 $O(\log N)$ 的时间内求出答案。不过，在“区间修改”指令中，如果某个节点被修改区间 $[l, r]$ 完全覆盖，那么以该节点为根的整棵子树中的所有节点存储的信息都会发生变化，若逐一进行更新，将使得一次区间修改指令的时间复杂度增加到 $O(N)$ ，这是我们不能接受的。

试想，如果我们在一次修改指令中发现节点 $p$ 代表的区间 $[p_l, p_r]$ 被修改区间 $[l, r]$ 完全覆盖，并且逐一更新了子树 $p$ 中的所有节点，但是在之后的查询指令中却根本没有用到 $[l, r]$ 的子区间作为候选答案，那么更新 $p$ 的整棵子树就是徒劳的。

换言之，我们在执行修改指令时，同样可以在 $l \leq p_l \leq p_r \leq r$ 的情况下立即返回，只不过在回溯之前向节点 $p$ 增加一个标记，标识“该节点曾经被修改，但其子节点尚未被更新”。

如果在后续的指令中，需要从节点 $p$ 向下递归，我们再检查 $p$ 是否具有标记。若有标记，就根据标记信息更新 $p$ 的两个子节点，同时为 $p$ 的两个子节点增加标记，然后清除 $p$ 的标记。

也就是说，除了在修改指令中直接划分成的 $O(\log N)$ 个节点之外，对任意节点的修改都延迟到“在后续操作中递归进入它的父节点时”再执行。这样一来，每条查询或修改指令的时间复杂度都降低到了 $O(\log N)$ 。这些标记就称为“延迟标记”。延迟标记提供了线段树中从上往下传递信息的方式。这种“延迟”也是设计算法与解决问题的一个重要思路。

【例题】A Simple Problem with Integers POJ3468

给定长度为 $N(N\leq 10^{5})$ 的数列A，然后输入 $Q(Q\leq 10^{5})$ 行操作指令。

第一类指令形如“C l r d”，表示把数列中第 $l \sim r$ 个数都加 $d$ 。

第二类指令形如“Q $l$ r”，表示询问数列中第 $l\sim r$ 个数的和。

在上一节中我们用树状数组解决了该问题，本节我们改用线段树来求解。除了左右端点 $l, r$ 以外，线段树的每个节点上保存了 sum（区间和）、add（增量延迟标记）两

个值。建树、查询和修改的框架仍然不变，spread函数实现了延迟标记的向下传递。

需要指出的是，延迟标记的含义为“该节点曾经被修改，但其子节点尚未被更新”，即延迟标记标识的是子节点等待更新的情况。因此，一个节点被打上“延迟标记”的同时，它自身保存的信息应该已经被修改完毕。读者在编写代码时，一定要注意“更新信息”与“打标记”之间的关系，避免出现错误。

struct SegmentTree {
    int l, r;
    long long sum, add;
    #define l(x) tree[x].l
    #define r(x) tree[x].r
    #define sum(x) tree[x].sum
    #define add(x) tree[x].add
} tree[100010*4];
int a[100010], n, m;
void build(int p, int l, int r) {
    l(p) = l, r(p) = r;
    if (l == r) { sum(p) = a[l]; return; }
    int mid = (l + r)/2;
    build(p*2, l, mid);
    build(p*2+1, mid+1, r);
    sum(p) = sum(p*2) + sum(p*2+1);
}
void spread(int p) {
    if (add(p)) { // 节点p有标记
        sum(p*2) += add(p)*(r(p*2) - 1(p*2) + 1); // 更新左子节点信息
        sum(p*2+1) += add(p)*(r(p*2+1) - 1(p*2+1) + 1); // 更新右子节点
        add(p*2) += add(p); // 给左子节点打延迟标记
        add(p*2+1) += add(p); // 给右子节点打延迟标记
        add(p) = 0; // 清除p的标记
    }
}

add(p) += d; //给节点打延迟标记
return;
}
spread(p); //下传延迟标记
int mid = (l(p) + r(p)) / 2;
if (l <= mid) change(p*2, l, r, d);
if (r > mid) change(p*2+1, l, r, d);
sum(p) = sum(p*2) + sum(p*2+1);
}
long long ask(int p, int l, int r) {
if (l <= l(p) && r >= r(p)) return sum(p);
spread(p); //下传延迟标记
int mid = (l(p) + r(p)) / 2;
long long val = 0;
if (l <= mid) val += ask(p*2, l, r);
if (r > mid) val += ask(p*2+1, l, r);
return val;
}
int main() {
cin >> n >> m;
for (int i=1; i<=n; i++) scanf("%d", &a[i]);
build(1, 1, n);
while (m--)
{
char op[2]; int l, r, d;
scanf("%s%d%d", op, &l, &r);
if(op[0] == 'C')
{
scanf("%d", &d);
change(1, l, r, d);
}
else printf("%lld\n", ask(1, l, r));
}

扫描线

【例题】Atlantis POJ1151

给定平面直角坐标系中的 $N$ 个矩形，求它们的面积并，即这些矩形的并集在坐标系中覆盖的总面积，如下图所示。

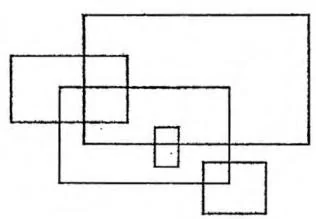
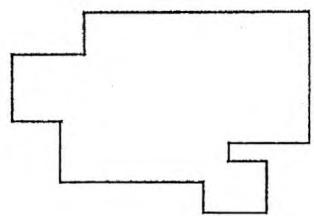
试想，如果我们用一条竖直直线从左到右扫过整个坐标系，那么直线上被并集图形覆盖的长度只会在每个矩形的左右边界处发生变化。

换言之，整个并集图形可以被分成 $2*N$ 段，每一段在直线上覆盖的长度（记为 $L$ ）是固定的，因此该段的面积就是 $L*$ 该段的宽度，各段面积之和即为所求。这根直线就被称为扫描线，这种解题思路被称为扫描线法。

具体来说，我们可以取出 $N$ 个矩形的左右边界。若一个矩形的两个对角顶点坐标为 $(x_{1},y_{1})$ 和 $(x_{2},y_{2})$ ，不妨设 $x_{1} < x_{2},y_{1} < y_{2}$ ，则左边界记为四元组 $(x_{1},y_{1},y_{2},1)$ 右边界记为四元组 $(x_{2},y_{1},y_{2}, - 1)$ 。把这 $2N$ 个四元组按照 $x$ 递增排序，如下图所示。

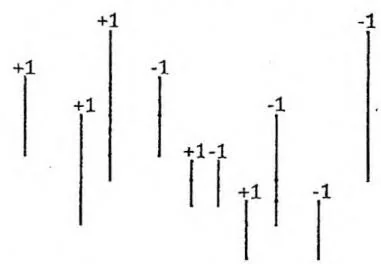
注意到本题中的 $y$ 坐标范围较大且不一定是整数，我们先把输入数据中出现的所有 $y$ 坐标放入一个数组，排序、去重，完成离散化。设 $\text{val}(y)$ 表示 $y$ 被离散化之后映射到的整数值， $\text{raw}(i)$ 表示整数值 $i$ 对应的原始 $y$ 坐标值。

在离散化后，若有 $M$ 个不同的 $y$ 坐标值，分别对应 $\text{raw}(1), \text{raw}(2), \dots, \text{raw}(M)$ ，则扫描线至多被分成 $M - 1$ 段，其中第 $i$ 段为区间 $[\text{raw}(i), \text{raw}(i + 1)]$ 。建立数组 $c$ ，用 $c[i]$ 记录扫描线上第 $i$ 段被覆盖的次数。起初 $c$ 数组中的元素全为0。

逐一扫描排序后的 $2N$ 个四元组，设当前四元组为 $(x, y_1, y_2, k)$ 。我们把数组 $c$ 中 $c[val(y_1)], c[val(y_1) + 1], \dots, c[val(y_2) - 1]$ 这些值都加 $k$ ，相当于覆盖了 $[y_1, y_2]$ 这个区间。此时，如果下一个四元组的横坐标为 $x_2$ ，则扫描线从 $x$ 扫到 $x_2$ 的过程中，

被覆盖的长度就固定为 $\sum_{c[i] > 0} \left( \text{raw}(i + 1) - \text{raw}(i) \right)$ ，即数组 $c$ 中至少被覆盖一次的“段”的总长度。于是，我们就让最终的答案 $\text{ans}$ 累加上 $(x_2 - x) * \sum_{c[i] > 0} \left( \text{raw}(i + 1) - \text{raw}(i) \right)$ 。

对于每个四元组，采用朴素算法在 $c$ 数组上执行修改与统计，即可在 $O(N^2)$ 的时间内求出并集图形的面积。

值得说明的是，四元组中的 $y_{1}, y_{2}$ 都是坐标，是一个“点”。我们需要维护的是扫描线上每一段被覆盖的次数及其长度，对“点”的覆盖次数进行统计是没有意义的。因此，我们把 $c$ 数组中的每个值 $c[i]$ 定义成扫描线上一个区间的覆盖次数，四元组 $(x, y_{1}, y_{2}, k)$ 对 $c[val(y_{1}) \sim val(y_{2}) - 1]$ 产生影响。读者在解题时一定要多加留意此类边界情况。

另外，我们可以用线段树维护 $c$ 数组，把算法优化到 $O(N \log N)$ 。

在本题中，我们只关心整个扫描线（线段树根节点）上被矩形覆盖的长度。而且，因为四元组 $(x, y_1, y_2, 1)$ 和 $(x, y_1, y_2, -1)$ 成对出现，所以线段树区间修改也是成对出现的。在这种特殊情形下，我们没有必要下传延迟标记，可以采用更为简单的做法。

除左右端点 $l, r$ 之外，在线段树的每个节点上维护两个值：该节点代表的区间被矩形覆盖的长度len，该节点自身被覆盖的次数cnt。最初，二者均为0。

对于一个四元组 $(x, y_1, y_2, k)$ ，我们在 $[val(y_1), val(y_2) - 1]$ 上执行区间修改。该区间被线段树划分成 $O(\log N)$ 个节点，我们把这些节点的 cnt 都加 $k$ 。

对于线段树中任意一个节点 $[l, r]$ , 若 $cnt > 0$ , 则 $dat$ 等于 $raw(r + 1) - raw(l)$ 。否则, 该点 $dat$ 等于两个子节点的 $dat$ 之和。在一个节点的 $cnt$ 值被修改, 以及线段树从下往上传递信息时, 我们都按照该方法更新 $dat$ 值。根节点的 $dat$ 值就是整个扫描线上被覆盖的长度。

【例题】Stars in Your Window POJ2482

在一个天空中有很多星星（看作平面直角坐标系），已知每颗星星的坐标和亮度（都是整数）。求用宽为 $w$ 、高为 $h$ 的矩形 $(w, h$ 为正整数）能圈住的星星的亮度总和最大是多少（矩形边界上的星星不算）。

因为矩形的大小固定，所以矩形可以由它的任意一个顶点唯一确定。我们可以考虑把矩形的右上角顶点放在什么位置，圈住的星星亮度总和最大。

对于一个星星 $(x, y, c)$ ，其中 $x, y$ 为坐标， $c$ 为亮度，“能圈住这颗星星的矩形右上角顶点坐标的范围”如下页图所示。该范围也是一个矩形，左下角顶点为 $(x, y)$ ，右上角顶点为 $(x + w, y + h)$ 。为了避免歧义，在接下来的讨论中，我们用“区域”一词来代指这个范围。

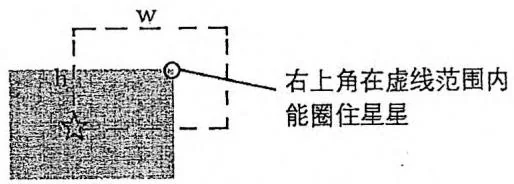
题目中说“矩形边界上的星星不算”。为了处理这种边界情况，不妨把所有星星向左、向下各移动0.5的距离，坐标从 $(x, y)$ 变为 $(x - 0.5, y - 0.5)$ 。在此基础上，不妨假设圈住星星的矩形顶点坐标都是整数。于是，上图虚线“区域”的左下角可看作 $(x, y)$ ，右上角可看作 $(x + w - 1, y + h - 1)$ ，边界也算在内。容易证明这些假设不会影响答案。

此时，问题转化为：平面上有若干个区域，每个区域都带有一个权值，求在哪个坐标上重叠的区域权值和最大。其中，每一个区域都是由一颗星星产生的，权值等于星星的亮度，把原问题中的矩形右上角放在该区域中，就能圈住这颗星星。

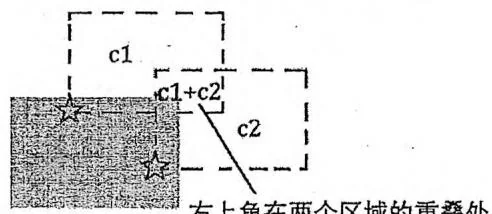
右上角在两个区域的重叠处

圈住c1+c2，亮度和最大

在转化后的问题中，我们使用扫描线算法，取出每个区域的左右边界，保存成2个四元组 $(x, y, y + h - 1, c)$ 和 $(x + w, y, y + h - 1, -c)$ 。把这些四元组按照横坐标（第一维的值）排序。

同时，关于纵坐标建立一棵线段树，维护区间最大值 $\text{dat}$ ，起初全为零。我们可以认为线段树上的一个值“ $y$ ”代表元区间 $[y, y + 1]$ ，而区间 $[y, y + h - 1]$ 可以表示为线段树中的 $y, y + 1, y + 2, \dots, y + h - 1$ 这几个值。这样一来，线段树维护的就是若干个数值构成的序列了。

逐一扫描每个四元组 $(x, y_1, y_2, c)$ ，在线段树中执行区间修改（可用延迟标记实现），把 $[y_1, y_2]$ 中的每个数都加 $c$ ，然后用根节点的 $dat$ 值更新答案即可。

0x43_线段树