0x42 树状数组
在 0×00 章的基本算法中,我们详细探讨了位运算、二分、倍增等贯穿于各种数据结构设计始末的思想。无论是二进制、折半还是翻倍,都与“二”这个数字密切相关。请读者回想 0×06 节的ST表,在对一个较大的连续线性范围进行统计时,我们把它按照2的整数次幂分成若干个小范围进行预处理和计算。再回想 0×01 节的快速幂算法,根据任意正整数关于2的不重复次幂的唯一分解性质,若一个正整数 x 的二进制表示为 ak−1ak−2⋯a2a1a0 ,其中等于1的位是 {ai1,ai2,⋯,aim} ,则正整数 x 可以被“二进制分解”成:
x=2i1+2i2+⋯+2im 不妨设 i1>i2>⋯>im ,进一步地,区间 [1,x] 可以分成 O(logx) 个小区间:
长度为 2i1 的小区间 [1,2i1]
长度为 2i2 的小区间 [2i1+1,2i1+2i2]
长度为 2i3 的小区间 [2i1+2i2+1,2i1+2i2+2i3]
··
m. 长度为 2im 的小区间 [2i1+2i2+⋯+2im−1+1,2i1+2i2+⋯+2im]
这些小区间的共同特点是:若区间结尾为 R ,则区间长度就等于 R 的“二进制分解”下最小的2的次幂,即lowbit (R) 。例如 x=7=22+21+20 ,区间[1,7]可以分成[1,4]、[5,6]和[7,7]三个小区间,长度分别是 lowbit(4)=4 、 lowbit(6)=2 和 lowbit(7)=1 。
我们在0x01节中探讨过lowbit运算,并介绍了如何利用lowbit运算找出整数在二进制表示下所有等于1的位。类似地,给定一个整数 x ,下面这段代码可以计算出区间 [1,x] 分成的 O(logx) 个小区间:
while $(x > 0)$ { printf("%d, %d]\n", x - (x & -x) + 1, x); x -= x & -x; }
树状数组(Binary Indexed Trees)就是一种基于上述思想的数据结构,其基本用途是维护序列的前缀和。对于给定的序列 a ,我们建立一个数组 c ,其中 c[x] 保存序列 a 的区间 [x−lowbit(x)+1,x] 中所有数的和,即 ∑i=x−lowbit(x)+1xa[i] 。
事实上,数组 c 可以看作一个如下图所示的树形结构,图中最下边一行是 N 个叶节点( N=16 ),代表数值 a[1∼N] 。该结构满足以下性质:
每个内部节点 c[x] 保存以它为根的子树中所有叶节点的和。
每个内部节点 c[x] 的子节点个数等于 lowbit (x) 的位数。
除树根外,每个内部节点 c[x] 的父节点是 c[x+lowbit(x)] 。
树的深度为 O(logN) 。
如果 N 不是2的整次幂,那么树状数组就是一个具有同样性质的森林结构。

树状数组支持的基本操作有两个,第一个操作是查询前缀和,即序列 a 第 1∼x 个数的和。按照我们刚才提出的方法,应该求出 x 的二进制表示中每个等于 1 的位,把 [1,x] 分成 O(logN) 个小区间,而每个小区间的区间和都已经保存在数组 c 中。所以,把上面的代码稍加改写即可在 O(logN) 的时间内查询前缀和:
int ask(int x) { int ans $= 0$ for $(\textsf{;x};\textsf{x} - = \textsf{x}\& \textsf{-x})$ ans $+ = c[x]$ return ans;
1
当然,若要查询序列 a 的区间 [l,r] 中所有数的和,只需计算 ask(r)−ask(l−1) 。
树状数组支持的第二个基本操作是单点增加,意思是给序列中的一个数 a[x] 加上 y ,同时正确维护序列的前缀和。根据上面给出的树形结构和它的性质,只有节点 c[x] 及其所有祖先节点保存的“区间和”包含 a[x] ,而任意一个节点的祖先至多只有 logN 个,我们逐一对它们的 c 值进行更新即可。下面的代码在 O(logN) 时间内执行单点增加操作:
void add(int x, int y) {
for ( ; x <= N; x += x & -x) c[x] += y;
}
在执行所有操作之前,我们需要对树状数组进行初始化——针对原始序列 a 构造一个树状数组。
为了简便,比较一般的初始化方法是:直接建立一个全为0的数组 c ,然后对每个位置 x 执行 add(x,a[x]) ,就完成了对原始序列 a 构造树状数组的过程,时间复杂度为 O(NlogN) 。通常采用这种初始化方法已经足够。
更高效的初始化方法是:从小到大依次考虑每个节点 x ,借助 lowbit 运算扫描它的子节点并求和。若采用这种方法,上面树形结构中的每条边只会被遍历一次,时间复杂度为 O(∑k=1logNk∗N/2k)=O(N) 。
树状数组与逆序对
任意给定一个集合 a ,如果用 t[val] 保存数值 val 在集合 a 中出现的次数,那么数组 t 在 [l,r] 上的区间和(即 ∑i=lrt[i] )就表示集合 a 中范围在 [l,r] 内的数有多少个。
我们可以在集合 a 的数值范围上建立一个树状数组,来维护 t 的前缀和。这样即使在集合 a 中插入或删除一个数,也可以高效地进行统计。
我们在 0×05 节中提到了逆序对问题以及使用归并排序的解法。对于一个序列 a ,
若 i<j 且 a[i]>a[j] ,则称 a[i] 与 a[j] 构成逆序对。按照上述思路,利用树状数组也可以求出一个序列的逆序对个数:
在序列 a 的数值范围上建立树状数组,初始化为全零。
倒序扫描给定的序列 a ,对于每个数 a[i] :
(1) 在树状数组中查询前缀和 [1,a[i]−1] ,累加到答案 ans 中。
(2) 执行“单点增加”操作,即把位置 a[i] 上的数加1(相当于 t[a[i]++) ,同时正确维护 t 的前缀和。这表示数值 a[i] 又出现了1次。
ans 即为所求。
for (int i = n; i; i--) {
ans += ask(a[i] - 1);
add(a[i], 1);
}
在这个算法中,因为倒序扫描,“已经出现过的数”就是在 a[i] 后边的数,所以我们通过树状数组查询的内容就是“每个 a[i] 后边有多少个比它小”。每次查询的结果之和当然就是逆序对个数。时间复杂度为 O((N+M)logM) , M 为数值范围的大小。
当数值范围较大时,当然可以先进行离散化,再用树状数组进行计算。不过因为离散化本身就要通过排序来实现,所以在这种情况下就不如直接用归并排序来计算逆序对数了。
【例题】楼兰图腾 TYVJ1432
平面上有 N(N≤105) 个点,每个点的横、纵坐标的范围都是 1∼N ,任意两个点的横、纵坐标都不相同。
若三个点 (x1,y1),(x2,y2),(x3,y3) 满足 x1<x2<x3 , y1>y2 并且 y3>y2 , 则称这三个点构成“v”字图腾。
若三个点 (x1,y1),(x2,y2),(x3,y3) 满足 x1<x2<x3,y1<y2 并且 y3<y2 ,则称这三个点构成“ ∧ ”字图腾。
求平面上“v”和“ ∧ ”字图腾的个数。
题目描述的第一句话实际上告诉我们,如果把这 N 个点按照横坐标排序,那么它们的纵坐标是 1∼N 的一个排列。我们把这个排列记为 a 。
在树状数组求逆序对的算法中,我们已经知道如何在一个序列中计算每个数后边有多少个数比它小。类似地,我们可以:
倒序扫描序列 a ,利用树状数组求出每个 a[i] 后边有几个数比它大,记为 right[i]。
正序扫描序列 a ,利用树状数组求出每个 a[i] 前边有几个数比它大,记为 left[i]。
依次枚举每个点作为中间点,以该点为中心的“v”字图腾个数显然是left[i]*right[i]。所以“v”字图腾的总数就是 ∑i=1Nleft[i]∗right[i]
按照同样的方法,我们可以统计出“ ∧ ”字图腾的个数。
♠ 树状数组的扩展应用
【例题】A Tiny Problem with Integers
给定长度为 N(N≤105) 的数列 A ,然后输入 Q(Q≤105) 行操作指令。
第一类指令形如“C l r d”,表示把数列中第 l∼r 个数都加 d 。
第二类指令形如“Q x ”,表示询问数列中第 x 个数的值。
本题的指令有“区间增加”和“单点查询”,而树状数组仅支持“单点增加”,需要作出一些转化来解决问题。
新建一个数组 b ,起初为全零。对于每条指令“C lr d”,我们把它转化成以下两条指令:
把 b[l] 加上 d 。
再把 b[r+1] 减去 d 。
执行上面两条指令之后,我们来考虑一下 b 数组的前缀和( b[1∼x] 的和)的情况:
对于 1≤x<l ,前缀和不变。
对于 l≤x≤r ,前缀和增加了 d 。
对于 r<x≤N ,前缀和不变( l 处加 d , r+1 处减 d ,抵消)。
我们发现, b 数组的前缀和 b[1∼x] 就反映了指令“C l r d”对 a[x] 产生的影响。
于是,我们可以用树状数组来维护数组 b 的前缀和(对 b 只有单点增加操作)。因为各次操作之间具有可累加性,所以在树状数组上查询前缀和 b[1∼x] ,就得出了到目前为止所有“C”指令在 a[x] 上增加的数值总和。再加上 a[x] 的初始值,就得到了“Q x ”的答案。
初态
指令1
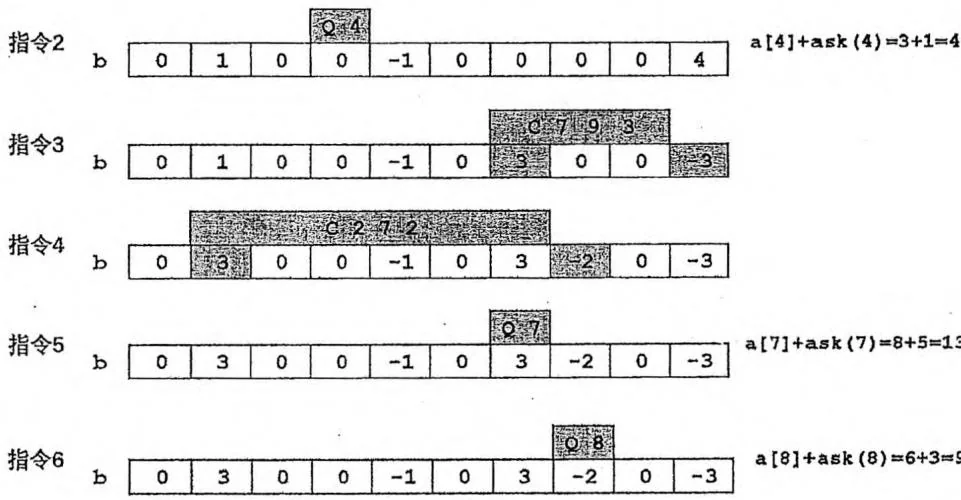
该做法把“维护数列的具体值”转化为“维护指令的累积影响”。每次修改的“影响”在 l 处产生,在 r+1 处消除。“影响”的前缀和 b[1∼x] 就代表了数值 a[x] 的变化情况,如上图所示。该做法巧妙地把“区间增加”+“单点查询”变为树状数组擅长的“单点增加”+“区间查询”进行处理。
【例题】A Simple Problem with Integers POJ3468
给定长度为 N(N≤105) 的数列A,然后输入 Q(Q≤105) 行操作指令。
第一类指令形如“C l r d”,表示把数列中第 l∼r 个数都加 d 。
第二类指令形如“Q l r”,表示询问数列中第 l˙∼r 个数的和。
在上一题中,我们用树状数组维护了一个数组 b ,对于每条指令“C l r d”,把 b[l] 加上 d ,再把 b[r+1] 减去 d 。
我们已经讨论过, b 数组的前缀和 ∑i=1xb[i] 就是经过这些指令后 a[x] 增加的值。那么序列 a 的前缀和 a[1∼x] 整体增加的值就是:
i=1∑xj=1∑ib[j] 上式可以改写为:
i=1∑xj=1∑ib[j]=i=1∑x(x−i+1)∗b[i]=(x+1)i=1∑xb[i]−i=1∑xi∗b[i] 这个推导也可以用图形来直观描绘:
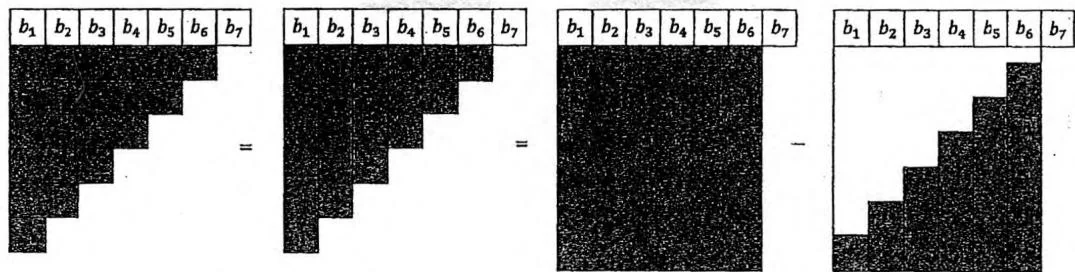
在本题中,我们增加一个树状数组,用于维护 i∗b[i] 的前缀和 ∑i=1xi∗b[i] ,上式就可以直接查询、计算了。
具体来说,我们建立两个树状数组 c0 和 c1 ,起初全部赋值为零。对于每条指令“C r d”,执行4个操作:
在树状数组 c0 中,把位置 l 上的数加 d 。
在树状数组 c0 中,把位置 r+1 上的数减 d 。
在树状数组 c1 中,把位置 l 上的数加 l∗d 。
在树状数组 c1 中,把位置 r+1 上的数减 (r+1)∗d 。
另外,我们建立数组 sum 存储序列 a 的原始前缀和。对于每条指令“Q l r”,当然还是拆成 1∼r 和 1∼l−1 两个部分,二者相减。写成式子就是:
(sum[r]+(r+1)∗ask(c0,r)−ask(c1,r))−(sum[l−1]+l∗ask(c1,l−1)−ask(c1,l−1)) const int SIZE=100010;
int a[SIZE],n,m;
long long c[2][SIZE],sum[SIZE];
long long ask(int k,int x) {
long long ans=0;
for(;x;x-=x&-x) ans+=c[k][x];
return ans;
}
void add(int k,int x,int y) {
for(;x<=n;x+=x&-x) c[k][x]+=y
}
int main() {
cin>>n>>m;
for(int i=1;i<=n;i++) {
scanf("%d",&a[i]);
}
};
sum[i]=sum[i-1]+a[i];
}
while(m--){ char op[2];int l,r,d; scanf("%s%d%d",op,&l,&r); if(op[0] == 'C') { scanf("%d",&d); add(0,l,d); add(0,r+1,-d); add(1,l,l\*d); add(1,r+1,-(r+1)\*d); } else{ long long ans=sum[r]+(r+1)*ask(0,r)-ask(1,r); ans-=sum[l-1]+l\*ask(0,l-1)-ask(1,l-1); printf("%lld\n",ans); } 1
值得指出的是,为什么我们把 ∑i=1x(x−i+1)∗b[i] 变成 (x+1)∑i=1xb[i]−∑i=1xi∗b[i] 进行统计呢?仔细观察该式的定义,这里的“ x ”是关于“前缀和 a[1∼x] ”这个询问的变量,而“ i ”是在每次修改时影响的对象。
对于前者来说,求和式中的每一项同时包含 x 和 i ,在修改时无法确定 (x−i+1) 的值,只能维护 b[i] 的前缀和。在询问时需要面临一个“系数为等差数列”的求和式,计算起来非常困难。
对于后者来说,求和式中的每一项只与 i 有关。它通过一次容斥,把 (x+1) 提取为常量,使得 b[i] 的前缀和与 i∗b[i] 的前缀和可以分别用树状数组进行维护。这种分离包含有多个变量的项,使公式中不同变量之间互相独立的思想非常重要,我们在下一章讨论动态规划的优化策略时会多次用到。
【例题】Lost Cows FOJ2182
有 n 头奶牛 (n≤105) ,已知它们的身高为 1∼n 且各不相同,但不知道每头奶牛的具体身高。
现在这 n 头奶牛站成一列,已知第 i 头奶牛前面有 Ai 头比它低,求每头奶牛的身高。
如果最后一头奶牛前面有 An 头牛比它高,那么显然它的身高 Hn=An+1 。
如果倒数第二头奶牛前有 An−1 头牛比它高, 那么:
若 An−1<An ,则它的身高 Hn−1=An−1+1 。
若 An−1≥An ,则它的身高 Hn−1=An−1+2 。
依此类推,如果第 k 头牛前面有 Ak 头比它高,那么它的身高 Hk 是数值 1∼n 中第 Ak+1 小的没有在 {Hk+1,Hk+2,…,Hn} 中出现过的数。
具体来说,我们建立一个长度为 n 的01序列 b ,起初全部为1。然后,从 n 到1倒序扫描每个 Ai ,对每个 Ai 执行以下两个操作:
查询序列 b 中第 Ai+1 个 1 在什么位置,这个位置号就是第 i 头奶牛的身高 Hi 。
把 b[Hi] 减 1(从 1 变为 0)。
也就是说,我们需要实时维护一个01序列,支持查询第 k 个1的位置( k 为任意整数),以及修改序列中的一个数值。
方法一:树状数组+二分,单次操作 O(log2n)
用树状数组 c 维护01序列 b 的前缀和,在每次查询时二分答案,通过 ask(mid) 即可得到前 mid 个数中有多少个1,与 k 比较大小,即可确定二分上下界的变化。
方法二:树状数组+倍增,单次操作 O(logn)
用树状数组 c 维护01序列 b 的前缀和,在每次查询时:
初始化两个变量 ans=0 和 sum=0 。
从 logn (下取整)到1倒序考虑每个整数 p 。
对 于 每 个p,若ans+2p≤n并 且sum+c[ans+2p]<k,则 令ans+=2p,sum+=c[ans+2p]∘ 最后, Hi=ans+1 即为所求。
该做法与0x06节“倍增”中给出的第一个小问题采用了类似的思想,都是“以2的整数次幂为步长;能累加则累加”。树状数组 c 恰好已经为我们维护了区间长度为2的次幂的一些信息,直接结合树状数组使用这种思想,就得到了上面这个高效算法。


