0x11栈

栈是一种“后进先出”的线性数据结构。栈只有一端能够进出元素，我们一般称这一端为栈顶，另一端为栈底。添加或删除栈中元素时，我们只能将其插入到栈顶（进栈），或者把栈顶元素从栈中取出（出栈）。

我们可以在 $\mathrm{C}++$ 中用一个数组和一个变量（记录栈顶位置）来实现栈结构。在之前的章节我们也提到过，栈是机器实现递归（深度优先搜索）的基本结构。读者对于栈的基本用法应该已经比较熟悉，这里就不再赘述，而是把更多篇幅放在栈的应用上。

【例题】Push, Pop, GetMin

实现一个栈，支持Push（入栈）、Pop（出栈并输出栈顶）和GetMin（查询栈中最小的值）三个操作，要求时间复杂度均为 $O(1)$ 。

栈结构原本就支持 O(1) 的入栈、出栈操作，但不支持查询最小值的操作。一个比较直接的思路是，我们知道二叉堆（第 0x17 节）是一种支持插入、取出堆顶、查询最值的数据结构，如果在维护一个栈的同时再维护一个存储同样元素的二叉堆，就可以支持题目中要求的操作。然而，它的时间复杂度是 $O(\log N)$ 。如果我们只用一个变量记录最小值，当发生出栈操作时，如果最小值恰好被出栈，就无法得知新的最小值是什么。这启发我们使用一个线性结构来保存历史上每个时刻的最小值，这样就可以在出栈后进行还原。

我们建立两个栈，栈 $A$ 存储原本的数据，栈 $B$ 存储栈 $A$ 中以栈底开头的每段数据的最小值，就像下面这样：

A:9215302←

B:9211100←

当执行 $\operatorname{Push}(x)$ 操作时，在 $A$ 中插入 $x$ ，在 $B$ 中插入 $\min(B$ 的栈顶数据， $x)$ 。在执行 Pop 操作时，在 $A$ 、 $B$ 中分别弹出栈顶。在执行 GetMin 操作时，直接输出 $B$ 的栈顶数据。每个操作的时间复杂度都是 $O(1)$ 。

【例题】Editor HDOJ4699

维护一个整数序列的编辑器，有以下五种操作，操作总数不超过 $10^{6}$ 。

I $x$ ：在当前光标位置之后插入一个整数 $x$ ，插入以后光标移动到 $x$ 之后；

D：删除光标之前的一个整数，即按下退格键Backspace；

L: 光标向左移动一个位置, 即按下 $\leftarrow$ 键;

R：光标向右移动一个位置，即按下 $\rightarrow$ 键；

Q $k$ ：询问在位置 $k$ 之前的最大前缀和，其中 $k$ 不超过当前光标的位置。

本题的特殊点在于，I,D,L,R四种操作都在光标位置处发生，并且操作完成后光标至多移动1个位置。根据这种“始终在序列中间某个指定位置进行修改”的性质，再联想到上一章我们动态维护中位数的“对顶堆”算法，我们不难想到一个类似的“对顶栈”做法。

建立两个栈，栈 $A$ 存储从序列开头到当前光标位置的这一段子序列，栈 $B$ 存储从当前光标位置到序列结尾的这一段子序列，二者都以光标所在的那一端作为栈顶。这两个栈合起来就保存了整个序列。因为查询操作的 $k$ 不超过光标位置，所以我们用一个数组 $f$ 维护栈 $A$ 的前缀和的最大值即可。设 $A$ 的栈顶位置下标是 $p_A$ ，sum 是序列 $A$ 的前缀和数组。

对于 $\mathbf{I}x$ 操作：

把 $x$ 插入栈 $A$
更新 $sum[p_A] = sum[p_A - 1] + A[p_A]$
更新 $f[p_A] = \max (f[p_A - 1], \text{sum}[p_A])$ 。

对于D操作，把 $A$ 的栈顶出栈。

对于L操作，弹出 $A$ 的栈顶，插入到 $B$ 中。

对于R操作：

弹出 B 的栈顶，插入到 A 中；
更新 $sum[p_A] = sum[p_A - 1] + A[p_A]$
更新 $f[p_A] = \max (f[p_A - 1], \text{sum}[p_A])$ 。

对于 $Qk$ 询问，直接返回 $f[k]$ 。

通过这样两个“对顶栈”，我们在O(1)的时间内实现了每种操作和询问。

【例题】进出栈序列问题

给定 $1 \sim N$ 这 $N$ 个整数和一个无限大的栈，每个数都要进栈并出栈一次。如果进栈的顺序为 $1,2,\dots,N$ ，那么可能的出栈序列有多少种？

相关题目：TYVJ1374/1363/1372/1336 火车进出栈问题

方法一：搜索（枚举/递归）， $0(2^{N})$

一个很直观的想法是，面对任何一个状态我们只有两种选择：

把下一个数进栈。
把当前栈顶的数出栈（如果栈非空）。

根据上一章学到的知识，我们可以枚举每一步如何选择，用递归实现这个规模为 $O(2^{N})$ 的枚举，这样就得到了所有可能的出栈序列方案。

方法二：递推， $O(N^{2})$

本题只要求我们计算出可能出栈序列有多少种，并不关心具体方案，于是我们可以使用递推直接进行统计。设 $S_N$ 表示进栈顺序为 $1, 2, \dots, N$ 时可能的出栈序列总数。根据递推的理论，我们需要想办法把问题分解成若干个类似的子问题。

考虑“1”这个数排在最终出栈序列中的位置，如果最后“1”这个数排在第 $k$ 个，那么整个序列的进出栈过程就是：

整数 1 入栈。
整数 $2 \sim k$ 这 $k - 1$ 个数按某种顺序进出栈。
整数 1 出栈，排在第 $k$ 个。
整数 $k + 1 \sim N$ 这 $N - k$ 个数按某种顺序进出栈。

于是整个问题就被“1”这个数划分成了“ $k - 1$ 个数进出栈”和“ $N - k$ 个数进出栈”这两个子问题，得到递推公式：

S _ {N} = \sum_ {k = 1} ^ {N} S _ {k - 1} * S _ {N - k}

方法三：动态规划， $O(N^{2})$

在任何一个时刻，我们实际上只关心有多少个数尚未入栈、有多少个数还在栈里，并做出一步合法的操作，并不关心这些数具体是哪些。因此，我们可以用 $F[i, j]$ 表示有 $i$ 个数尚未进栈，目前有 $j$ 个数在栈里，已经有 $n - i - j$ 个数出栈时的方案总数。

在最终状态下，即所有数已经出栈时，顺序已经确定，所以边界为： $F[0,0] = 1$ 。

我们需要求出初始状态下，即所有数尚未进栈时，可以到达上述边界的方案总数，所以目标为： $F[N,0]$ 。

每一步的两种决策分别是“把一个数进栈”和“把栈顶的数出栈”，所以有公式：

F [ i, j ] = F [ i - 1, j + 1 ] + F [ i, j - 1 ]

方法四：数学， $O(N)$

该问题等价于求第 $N$ 项Catalan数，即 $C_{2N}^{N} / (N - 1)$ 。我们将在第0x36节详细介绍。

$\spadesuit$ 表达式计算

栈的一大用处是做算术表达式的计算。算术表达式通常有前缀、中缀、后缀三种表示方法。

中缀表达式，是我们最常见的表达式，例如： $3*(1 - 2)$

前缀表达式，又称波兰式，形如“op $A$ B”，其中 op 是一个运算符， $A, B$ 是另外两个前缀表达式。例如：*3-12。

后缀表达式，又称逆波兰式，形如“A B op”，例如：12-3*。

前缀和后缀表达式的值的定义是，先递归求出 $A, B$ 的值，二者再做 op 运算的结果。这两种表达式不需要使用括号，其运算方案是唯一确定的。对于计算机来讲，它最容易理解后缀表达式，我们可以使用栈来 $O(N)$ 地求出它的值。

后缀表达式求值

建立一个用于存数的栈，逐一扫描该后缀表达式中的元素。

(1) 如果遇到一个数，则把该数入栈。
(2) 如果遇到运算符，就取出栈顶的两个数进行计算，把结果入栈。

扫描完成后，栈中恰好剩下一个数，就是该后缀表达式的值。

读者可以模拟12-3*这个后缀表达式的计算过程进行体会。

如果想让计算机求解我们人类常用的中缀表达式的值，最快的办法就是把中缀表达式转化成后缀表达式，再使用上述方法求值。这个转化过程同样可以使用栈来 $O(N)$ 地完成。

中缀表达式转后缀表达式

建立一个用于存运算符的栈，逐一扫描该中缀表达式中的元素。

(1) 如果遇到一个数，输出该数。
(2) 如果遇到左括号，把左括号入栈。
(3) 如果遇到右括号，不断取出栈顶并输出，直到栈顶为左括号，然后把左括号出栈。

(4) 如果遇到运算符，只要栈顶符号的优先级不低于新符号，就不断取出栈顶并输出，最后把新符号进栈。优先级为乘除>加减>左括号。

依次取出并输出栈中的所有剩余符号，最终输出的序列就是一个与原中缀表达式等价的后缀表达式。

读者可以写一些稍微复杂的中缀表达式进行模拟，体会这个计算过程。

以上例子中包含的都是一位数，如果是多位数，并且表达式是使用字符串逐字符存储的，我们只需要稍加判断，把连续的一段数字看成一个数即可。

当然，我们也可以不转化成后缀表达式，而是使用递归法直接求解中缀表达式的值，时间复杂度为 $O(N^{2})$ 。

中缀表达式的递归法求值

目标：求解中缀表达式 $S[1\sim N]$ 的值。

子问题：求解中缀表达式 $S$ 的子区间表达式 $S[L \sim R]$ 的值。

在 $L \sim R$ 中考虑没有被任何括号包含的运算符：

(1) 若存在加减号，选其中最后一个，分成左右两半递归，结果相加减，返回。
(2) 若存在乘除号，选其中最后一个，分成左右两半递归，结果相乘除，返回。

若不存在没有被任何括号包含的运算符：

(1) 若首尾字符是括号，递归求解 $S[L + 1 \sim R - 1]$ ，把结果返回。
(2) 否则，说明区间 $S[L \sim R]$ 是一个数，直接返回数值。

读者可以用上面两种方法分别编程实现中缀表达式的求值。我们在配套光盘中给出了这些方法的参考程序。

单调栈

【例题】Largest Rectangle in a Histogram POJ2559

如下图所示，在一条水平线上方有若干个矩形，求包含于这些矩形的并集内部的最大矩形的面积（在下图中，答案就是阴影部分的面积），矩形个数 $\leq 10^{5}$ 。

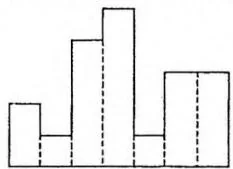
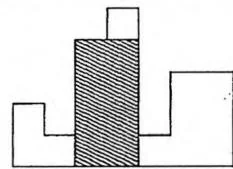
我们先来思考这样一个问题：如果矩形的高度从左到右单调递增，那么答案是多少？显而易见，我们可以尝试以每个矩形的高度作为最终矩形的高度，并把宽度延伸到右边界，得到一个矩形，在所有这样的矩形面积中取最大值就是答案。如下图所示：

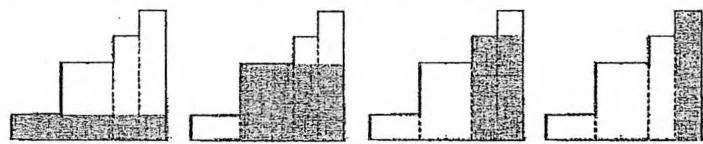
如果下一个矩形的高度比上一个小，那么该矩形想利用之前的矩形一起构成一块较大的面积时，这块面积的高度就不可能超过该矩形自己的高度。换句话说，在考虑完上图中的四种情况后，下图中打叉的那部分形状就没有丝毫用处了。

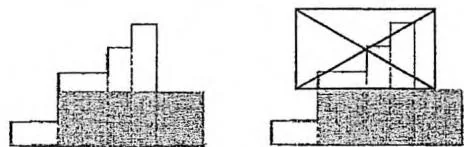
既然没有用处，为什么不把这些比该矩形高的矩形都删掉，用一个宽度累加、高度为该矩形自己的高度的新矩形（就是上图中的阴影部分）代替呢？这样并不会对后续的计算产生影响。于是我们维护的轮廓就变成了一个高度始终单调递增的矩形序列，问题变得可解了。

详细地说，我们建立一个栈，用来保存若干个矩形，这些矩形的高度是单调递增的。我们从左到右依次扫描每个矩形：

如果当前矩形比栈顶矩形高，直接进栈。

否则不断取出栈顶，直至栈为空或者栈顶矩形的高度比当前矩形小。在出栈过程中，我们累计被弹出的矩形的宽度之和，并且每弹出一个矩形，就用它的高度乘上累计的宽度去更新答案。整个出栈过程结束后，我们把一个高度为当前矩形高度、宽度为累计值的新矩形入栈。

整个扫描结束后，我们把栈中剩余的矩形依次弹出，按照与上面相同的方法更新答案。为了简化程序实现，也可以增加一个高度为0的矩形 $a[n + 1]$ ，以避免在扫描结束后栈中有剩余矩形。

$\mathsf{a}[\mathsf{n} + 1] = \mathsf{p} = 0;$    
for (int i  $= 1$  ;i  $\text{一} = \texttt{n} +1$  .i++) { if(a[i] > s[p]) {  $\mathsf{s}[^{+ + }\mathsf{p}] = \mathsf{a}[\mathsf{i}],\mathsf{w}[\mathsf{p}] = 1;$  ）else{ int width  $= 0$  · while(s[p] > a[i]) {

width  $+ = w[p]$  ans  $\equiv$  max(ans,(long long)width \* s[p]); p--; }  $\mathsf{s}[[ + + \mathsf{p}]] = \mathsf{a}[\mathsf{i}]$  ,w[p]  $\equiv$  width  $^+$  1; }

这就是著名的单调栈算法，时间复杂度为 $O(N)$ 。借助单调性处理问题的思想在于及时排除不可能的选项，保持策略集合的高度有效性和秩序性，从而为我们作出决策提供更多的条件和可能方法。

0x11_栈