12._矩阵可对角化_λ_的通俗解释

矩阵与对角形相似

在 特征值的几何意义 里说过，矩阵乘以一个向量，即$A \alpha$ 通常有两种理解： （1）可以看成矩阵$A$作用在向量 $\alpha$ 上，这使得 $\alpha$ 发生了旋转和缩放。 （2）把矩阵看成一个坐标系，$\alpha$是该坐标系里的一个向量。

在理解特征值与特征向量或矩阵相似时，有时候这2个概念会轮流切换。这个观点就像对物理中光的理解。物理课里，光有反射和衍射。当遇到反射时我们就用“粒子说”，把光子想象一个个小球进行理解。 当遇到干涉时，我们就使用“波动说”，把光子想象为波动，详见 高中物理

对于矩阵和向量相乘(甚至矩阵和矩阵相乘)，为了方便理解，本站给出了上面两种理解方式，这种理解到底是不是最优的，需要读者自行判断，或者您也可以由自己独特的见解。事实上，在《线性代数》数学这门课上，仅从数学的角度，他是不考虑意义的，比如特征值，数学教材就直接定义$A \alpha= \lambda \alpha$ ,此时$\lambda$ 就称作特征值，然后使用特征多项式求解，就完了。就像最简单的数字“1”，1就是1,1+1=2没什么好解释的，然而，为了理解他，我们会说，你有1个苹果，又拿了1个苹果，那么一共有2个苹果。这种人为的给数学赋予实际意义在帮助理解的同时，也会差生不同的解读，所以，就矩阵相似，读者也可以自己思考有没有更好的理解意义。

矩阵相似有4层理解： 第一层： $A \sim B$ ，即矩阵$P^{-1}AP=B$ 第二层： $A \sim \Lambda$ ，即矩阵$P^{-1}AP=\Lambda$ 第三层： $A \sim \Lambda$ 且 $A=A^T$ ，即矩阵$A$是对称矩阵，此时他相似对角形。可以看到，第三层是在第二层的基础上，进一步要求提高对称矩阵 第四层：在第三层的基础上，如果又满足 $A^T A=E$ 则称呼为正交变换，即$A$是对称矩阵，他的行列式的值为$\pm 1$.

{width=400px}

第一层：矩阵相似

$A$和$B$相似，这里的2个矩阵相当于2个参照物，或者更通俗的理解是2个小孩看一张图片，2个矩阵相当于2个小孩，在这种情况下要求最宽松。 {width=400px}

第二层：矩阵和对角形相似

矩阵$A$和对角形$\Lambda$相似，相当于一个小孩可以找到一个“正面视角”查看图片。 {width=400px}

第三层：对称矩阵和对角形相似

不是每个矩阵$A$都可以和对角形$\Lambda$相似，但是我们发现如果$A$是对称矩阵，则一定和对角形相似

{width=300px}

第四层：对称矩阵和正交矩阵相似

如果$A$是对称矩阵且$A$离物体的行列式的值为$1$或者$-1$，这种视角是最棒的，因为此时看图片不失真。我们把这种矩阵称作“正交矩阵”，使用正交矩阵进行的变换，叫做正交变换。

{width=400px}

为什么我们要花大力气找到正交变换？一句话：正交变换不改变图形的性质。

在正交变换里，会有一个典型例题，详见 正交变换

一个空间里有2个向量，使用正交变换时，不改变着2个向量的夹角和长度，如下，

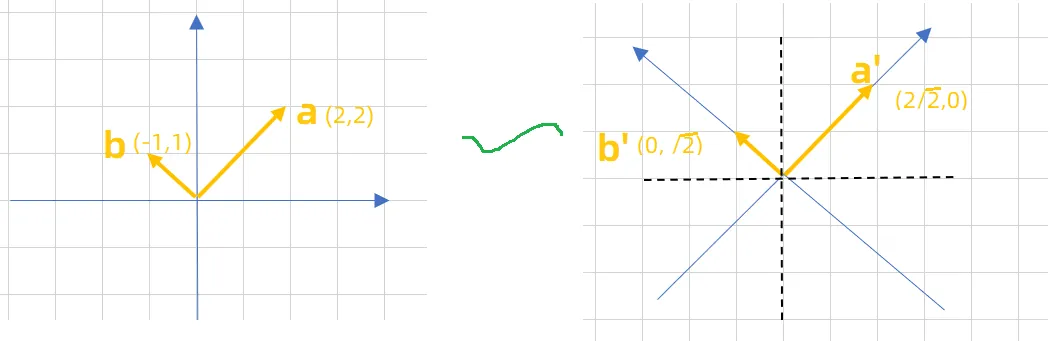
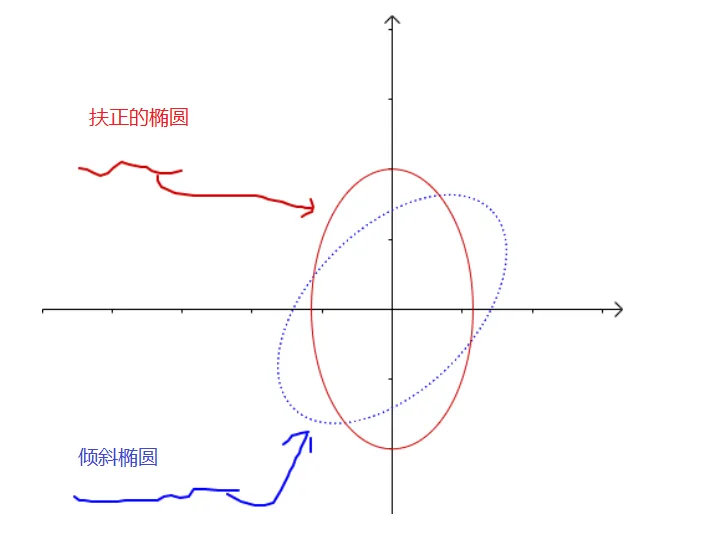
现在对上面进一步抽象，上面是2个向量，一个椭圆可以看成无数个向量组成的。假设有一个椭圆，在矩阵$A$表示下是斜椭圆，通过使用正交变换，就可以把他“扶正”，详见 特征值与特征向量

{width=400px}

哪些情况下矩阵可以对角化？

为方便理解，这里仅以三阶矩阵为例。

所谓矩阵可以对角化其实给你一个矩阵能找到一个“三维的空间直角坐标系”，这里的坐标单位分别是$a,b,c$ （如下示意） 矩阵可对角化包含了2个硬性要求： （1）原矩阵可以张成三维空间。 （2）新张成的三维空间必须能够互相垂直。

情况一： 矩阵有3个线性无关的特征向量。

下面用例题进行了演示 例 设矩阵$A=\left(\begin{array}{rrr}-2 & 1 & 1 \\0 & 2 & 0 \\-4 & 1 & 3\end{array}\right)$求他的特征与特征向量

解 ： 具体解法请参考 矩阵对角化 里的例1。

我们已经求的 $A$ 的特征值为 $\lambda_1=-1, \lambda_2=\lambda_3=2$ ．

和对应的的特征向量

现在想想一下你在三维空间里，原坐标系是

通过特征值和特征向量，我们找到了一个对角矩阵

, 在$\Lambda$的空间里，因为 $\lambda_1=-1$ 所以，沿$x$方向方向相反，而 $\lambda_2=2, \lambda_3=2$， 所以，沿着$y,z$方向，进行了拉伸，参考下图。

下图右图小男孩看起来就漂亮多了

所以，矩阵相可对角化可以理解为，通过矩阵A观察一个几何体，我们可以找到一个三维对角形坐标系。在这个坐标系里，每个坐标轴上的特征值对应相应坐标系上放大或者缩小的倍数，在这个坐标系里，看到的物体更简洁、明了

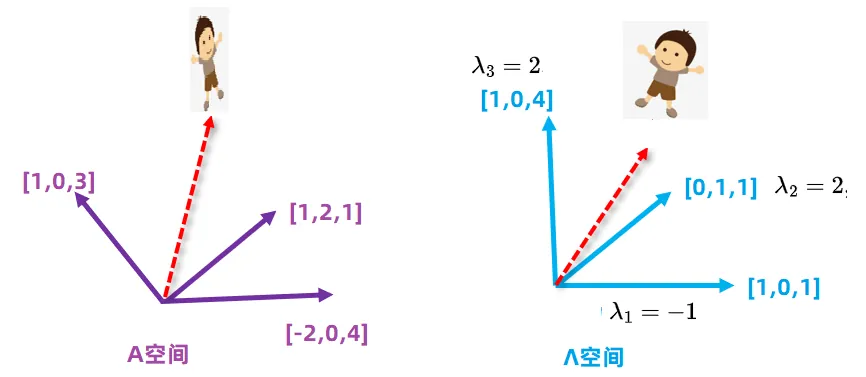
从上图可以看到矩阵A3个列向量被映射为对角形矩阵3个对应坐标系，在对角线视角下观察几何体，几何体更简洁。

推理有3个不同的特征值。

我们可以这么理解，矩阵的每一列被映射为对角形的每一列，特征值代表映射后缩放的倍数，如果特征值不同，根据特征值，就很容易知道矩阵A的哪一列对应对角形的哪一列，所以可以对角化。

如果把特征值比喻三把不同的钥匙，把特征向量比喻为3个不同的锁，那么因为每把钥匙不同，自然就能找到对用的不同的3吧

{widht=300px}

情况三：对称矩阵可以对角化。

我们知道对于一个方阵，他本质是一个二维表格，矩阵对角化就是对矩阵进行缩放，而如果是对称矩阵，相当于二维表格在$x,y$同比放大或缩小相同的倍数，他保持了图形比例性不变。

情况四：特征值有重根，此时矩阵可能可以对角化也可能不能对角化。

如果矩阵$A$是三个向量$\alpha1,\alpha2,\alpha2$，对角形是$\lambda1,\lambda2,\lambda3$，而特征值是$1,2,2$ 如果映射正好是1对1，此时就可以对角化。

{width=300px}

$\alpha1 \to 1 * \lambda1$ $\alpha2 \to 2 * \lambda2$ $\alpha3 \to 2 * \lambda3$

这种情况就可以对角化。

而如果变成 $\alpha1 \to 1 * \lambda1$ $\alpha2 \to 2 * \lambda3$ $\alpha3 \to 2 * \lambda3$

可以看到，最终只找到了2个向量，无法张成三维空间，自然就无法对角化。

{width=300px}

哪些情况矩阵无法对角化？

情况1：矩阵A本身无法张成三维空间。这又分两种 （1）矩阵A三个向量成比例共线 取一个极端的例子：

这个A的三个分量都是$(1,1,1)$ 是一个向量，他显然无法张成三维空间，自然不能其它他可以张成三维空间。

（2）矩阵A三个向量共面 此时自然也无法张成三维空间。

（3）对于上三角型矩阵，若主对角线上的元素全部一样，该上三角型矩阵不可对角化， 例如设矩阵 $A=\left(\begin{array}{cccc}\lambda_0 & a_{12} & \ldots & a_{1 n} \\ 0 & \lambda_0 & \ldots & a_{2 n} \\ \ldots & \ldots & \ldots & \ldots \\ 0 & 0 & \ldots & \lambda_0\end{array}\right)$ ，若矩阵相似于某个对角矩阵 $B$ ，下面讨论对角矩阵 $B$ 的对角元素到底如何．

首先容易得出 $\operatorname{tr}(A)=n \lambda_0,|A|=\left(\lambda_0\right)^n$ ，由矩阵相似的性质可以得到 $\operatorname{tr}(B)=n \lambda_0$ ， $|B|=\left(\lambda_0\right)^n$ ，而矩阵 $B$ 为对角矩阵，所以 $B=\left(\begin{array}{cccc}\lambda_0 & 0 & \ldots & 0 \\ 0 & \lambda_0 & \ldots & 0 \\ \ldots & \ldots & \ldots & \ldots \\ 0 & 0 & \ldots & \lambda_0\end{array}\right)=\lambda_0 E$ ，而这是不可能的，因为数量矩阵只能与自身相似，下面来说明一下这样的事实：

设 $\lambda_0 E \sim C$ ，即存在一个 $n$ 阶可逆方阵 $P$ ，使得 $P^{-1} \lambda_0 E P=C$ ，于是 $C=\lambda_0 E$ ，证毕。

例如：$\left(\begin{array}{lll}1 & 1 & 2 \\ 0 & 2 & 1 \\ 0 & 0 & 0\end{array}\right)$ 可以与对角阵相似，但 $\left(\begin{array}{lll}1 & 1 & 2 \\ 0 & 1 & 1 \\ 0 & 0 & 1\end{array}\right)$ 不可以与对角阵相似．

另外，当矩阵作用向量时，有可能产生空间亏损，此时就无法对角化。更详细说明参考下一节

经典退化的例子

最典型的不可对角化矩阵是如下的 Jordan Block（若尔当块）：

让我们来分析它：

1. 求特征值： 特征多项式为 $\det(A - \lambda I) = \det\begin{pmatrix} 2-\lambda & 1 \\ 0 & 2-\lambda \end{pmatrix} = (2-\lambda)^2$。 所以，它有一个特征值 $\lambda = 2$，代数重数为 2。

2. 求特征向量（几何重数）： 解方程组 $(A - 2I)\mathbf{v} = \mathbf{0}$：

这个方程等价于 $v_2 = 0$。所以，解向量具有形式 $\mathbf{v} = \begin{pmatrix} k \\ 0 \end{pmatrix} = k \begin{pmatrix} 1 \\ 0 \end{pmatrix}$。

1. 分析重数：

• 代数重数：2

• 几何重数：基础解系只有一个向量 $\begin{pmatrix} 1 \\ 0 \end{pmatrix}$，所以几何重数为 1。

结论：由于几何重数 (1) < 代数重数 (2)，这个矩阵无法找到两个线性无关的特征向量。它所有的特征向量都落在同一条直线 $\text{span}\left\{ \begin{pmatrix} 1 \\ 0 \end{pmatrix} \right\}$ 上。我们无法用特征向量构成一个覆盖整个二维平面的基，因此它不能被对角化。

几何解释：这个矩阵代表的线性变换是一个“剪切”变换，详见剪切变换。它把所有向量都向 $x$-轴方向“推倒”。你可以想象，在整个平面上，只有一个方向（$x$-轴方向）的向量被纯粹地拉伸了。其他方向的向量不仅被拉伸，方向也发生了改变。因此，不存在一个由纯粹伸缩方向（特征方向）构成的坐标系。

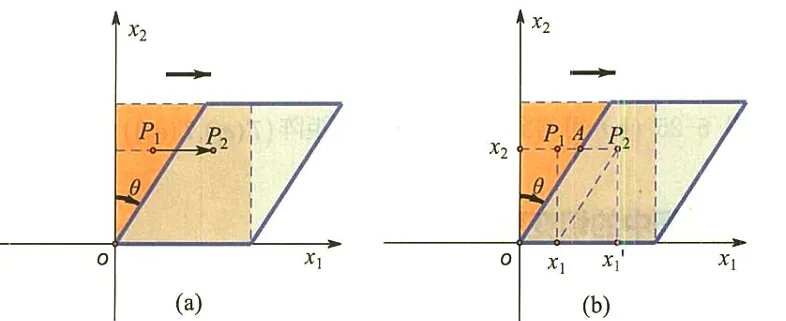
4. 更深层的视角：若尔当标准型 (Jordan Normal Form)

对于那些不能对角化的矩阵，我们也有一个“最接近对角形”的标准形式，称为若尔当标准型。

• 可对角化矩阵的若尔当标准型就是一个纯粹的对角矩阵 $\Lambda$。

• 不可对角化矩阵的若尔当标准型是由 若尔当块 构成的分块对角矩阵。

在我们上面的例子 $A = \begin{pmatrix} 2 & 1 \\ 0 & 2 \end{pmatrix}$ 中，它本身就是一个若尔当块。它已经是最简形式，无法再进一步对角化了。

若尔当块中的非对角线上那个“1”，就是阻碍对角化的“罪魁祸首”，它代表了特征向量短缺的程度，也引入了幂零的成分。

所以，当你问为什么有些矩阵不能对角化时，最核心的回答是：因为它们“缺”特征向量，无法形成一个完整的特征基，从而无法在新的坐标系下表现为纯粹的伸缩变换。 这些矩阵所代表的线性变换，其内在结构比简单的伸缩更为复杂，包含了“剪切”或“旋转”的成分，这些成分无法通过改变坐标系来消除。

总结

所以，当你问为什么有些矩阵不能对角化时，最核心的回答是：因为它们“缺”特征向量，无法形成一个完整的特征基，从而无法在新的坐标系下表现为纯粹的伸缩变换。 这些矩阵所代表的线性变换，其内在结构比简单的伸缩更为复杂，包含了“剪切”或“旋转”的成分，这些成分无法通过改变坐标系来消除。

例题

$n$ 阶矩阵 $A$ 与对角矩阵相似的判定条件

| 条件 |结论 | | -----| -----| ----| | 充分条件 |有n个不同特征值 $A$ 为实对称矩阵 | | 必要条件 | 代数重根的数量等于 r(λE-A) | | 充分必要条件 | $A$ 有 $n$ 个线性无关的特征向量 |

例下列矩阵中不能相似于对角矩阵的是（ ） （A）$\left(\begin{array}{lll}1 & 1 & a \\ 0 & 2 & 2 \\ 0 & 0 & 3\end{array}\right)$ （B）$\left(\begin{array}{lll}1 & 1 & a \\ 1 & 2 & 0 \\ a & 0 & 3\end{array}\right)$ （C）$\left(\begin{array}{lll}1 & 1 & a \\ 0 & 2 & 0 \\ 0 & 0 & 2\end{array}\right)$ （D）$\left(\begin{array}{lll}1 & 1 & a \\ 0 & 2 & 2 \\ 0 & 0 & 2\end{array}\right)$

解： （1）对称矩阵一定可以对角化，所以排除B （2）不同特征值一定可以对角化，所以排除A （对角形的对角线上的值为特征值，1，2，3 互不相同 ） 排除A

现在看C和D

对于C

有2个线性无关的特征向量，可以对角化。

对于D

有1个线性无关的特征向量，可以对角化。