1._方程组解公式汇总

线性代数中的三种变换-对立与统一

图片

图片

图片

图片

图片

图片

图片

图片

注①： 公式汇总主要参考 武忠祥 编制的 线性代数公式 注②： 图片汇总注意参考 西安电子科技大学教授杨威PPT，详见B站 线帒杨

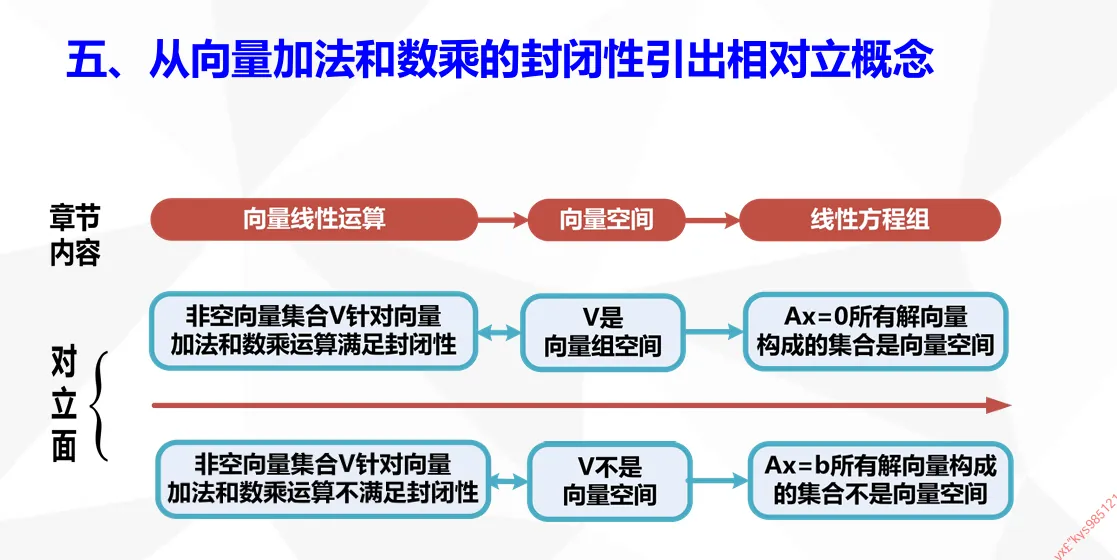
线性方程组解的个数

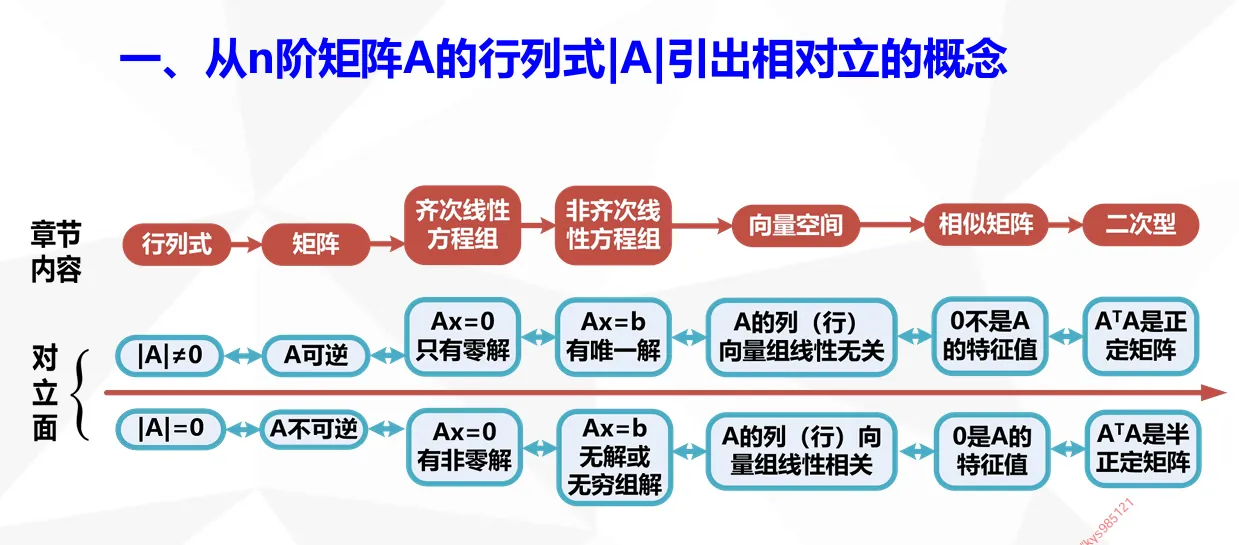
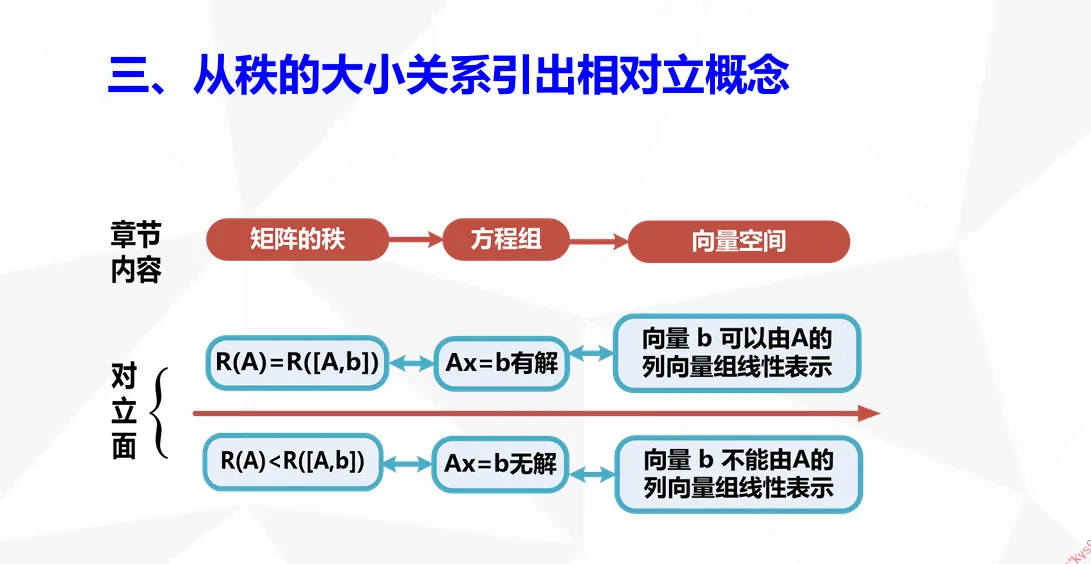
nn 元线性方程组 Ax=b\boldsymbol{A} \boldsymbol{x}=\boldsymbol{b}

①无解 ⇔r(A)<r(A,b)\Leftrightarrow \mathrm{r}(\boldsymbol{A})<\mathrm{r}(\boldsymbol{A}, \boldsymbol{b}). ②有唯一解 ⇔r(A)=r(A,b)=n\Leftrightarrow \mathrm{r}(\boldsymbol{A})=\mathrm{r}(\boldsymbol{A}, \boldsymbol{b})=n. ③有无穷多解 ⇔r(A)=r(A,b)<n\Leftrightarrow \mathrm{r}(\boldsymbol{A})=\mathrm{r}(\boldsymbol{A}, \boldsymbol{b})< n .

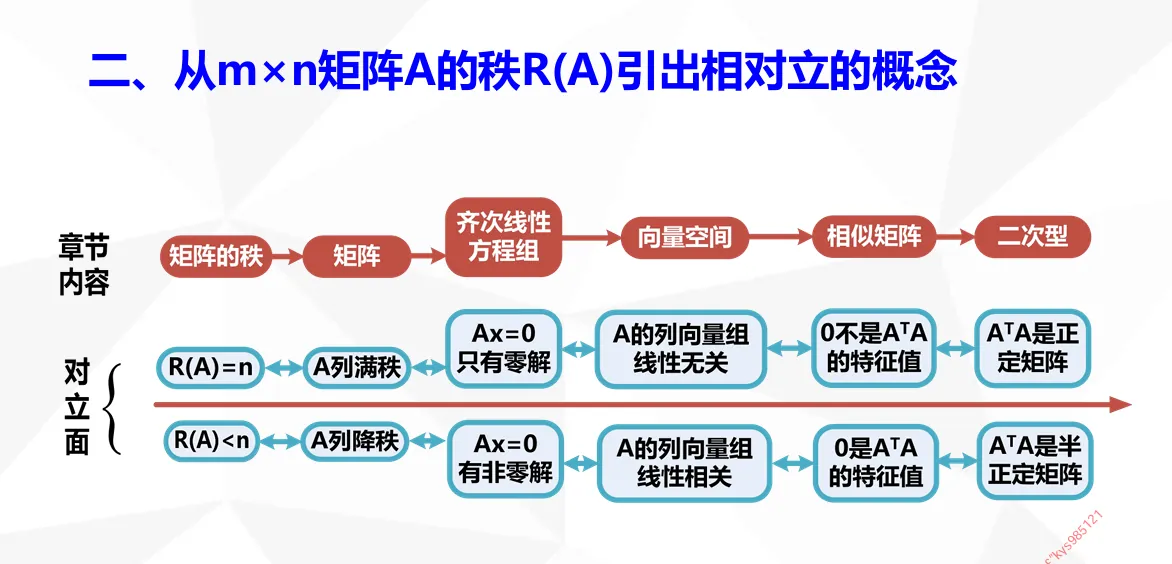
nn 元齐次线性方程组 Ax=0\boldsymbol{A} \boldsymbol{x}=\mathbf{0}

①只有零解 ⇔r(A)=n\Leftrightarrow \mathrm{r}(\boldsymbol{A})=n ②有非零解 ⇔r(A)<n\Leftrightarrow \mathrm{r}(A) < n

线性方程组解的性质

(1)若 ξ1,ξ2\xi_1, \boldsymbol{\xi}_2 是 Ax=0\boldsymbol{A x}=\mathbf{0} 的解, 则 ξ1+ξ2\xi_1+\xi_2 也是 Ax=0\boldsymbol{A x}=\mathbf{0} 的解.

(2)若 ξ\xi 是 Ax=0\boldsymbol{A} \boldsymbol{x}=\mathbf{0} 的解, k∈Rk \in R, 则 kξk \xi 也是 Ax=0\boldsymbol{A x}=\mathbf{0} 的解.

(3)若 η1,η2\boldsymbol{\eta}_1, \boldsymbol{\eta}_2 是 Ax=b\boldsymbol{A} \boldsymbol{x}=\boldsymbol{b} 的解, 则 η1−η2\boldsymbol{\eta}_1-\boldsymbol{\eta}_2 是对应的齐次线性方程组 Ax=0\boldsymbol{A} \boldsymbol{x}=\mathbf{0} 的解.

(4)若 η\boldsymbol{\eta} 是 Ax=b\boldsymbol{A x}=\boldsymbol{b} 的解, ξ\boldsymbol{\xi} 是 Ax=0\boldsymbol{A x}=\mathbf{0} 的解, 则 ξ+η\boldsymbol{\xi}+\boldsymbol{\eta} 是 Ax=b\boldsymbol{A x}=\boldsymbol{b} 的解.

(5)若 η1,η2,⋯ ,ηt\boldsymbol{\eta}_1, \boldsymbol{\eta}_2, \cdots, \boldsymbol{\eta}_t 是 Ax=b\boldsymbol{A} \boldsymbol{x}=\boldsymbol{b} 的解，则 当 k1+k2+⋯+kt=0k_1+k_2+\cdots+k_t=0 时, k1η1+k2η2+⋯+ktηtk_1 \boldsymbol{\eta}_1+k_2 \boldsymbol{\eta}_2+\cdots+k_t \boldsymbol{\eta}_t 是 Ax=0\boldsymbol{A x}=\mathbf{0} 的解. 当 k1+k2+⋯+kt=1k_1+k_2+\cdots+k_t=1 时, k1η1+k2η2+⋯+ktηtk_1 \boldsymbol{\eta}_1+k_2 \boldsymbol{\eta}_2+\cdots+k_t \boldsymbol{\eta}_t 是 Ax=b\boldsymbol{A} \boldsymbol{x}=\boldsymbol{b} 的解.

线性方程组解的结构

(1) 设 r(A)=r,ξ1,ξ2,⋯ ,ξn−r\mathrm{r}(\boldsymbol{A})=r, \boldsymbol{\xi}_1, \boldsymbol{\xi}_2, \cdots, \boldsymbol{\xi}_{n-\mathrm{r}} 是齐次线性方程组 Ax=0\boldsymbol{A} \boldsymbol{x}=\mathbf{0} 的一个基础解系, 则 Ax=0\boldsymbol{A} \boldsymbol{x}=\mathbf{0} 的通解为

x=k1ξ1+k2ξ2+⋯+kn−rξn−r(k1,k2,⋯ ,kn−r 是任意常数 ).\boldsymbol{x}=k_1 \xi_1+k_2 \xi_2+\cdots+k_{n-r} \boldsymbol{\xi}_{n-r}\left(k_1, k_2, \cdots, k_{n-r} \text { 是任意常数 }\right) .

(2) 设 η∗\boldsymbol{\eta}^* 是 Ax=b\boldsymbol{A} \boldsymbol{x}=\boldsymbol{b} 的一个特解， ξ1,ξ2,⋯ ,ξn−r\boldsymbol{\xi}_1, \boldsymbol{\xi}_2, \cdots, \boldsymbol{\xi}_{n-\mathrm{r}} 是对应的齐次线性方程组 Ax=0\boldsymbol{A} \boldsymbol{x}=\mathbf{0} 的一 个基础解系, 则 Ax=b\boldsymbol{A} \boldsymbol{x}=\boldsymbol{b} 的通解为

x=k1ξ1+k2ξ2+⋯+kn−rξn−r+η∗(k1,k2,⋯kn−r 是任意常数 ).\boldsymbol{x}=k_1 \xi_1+k_2 \xi_2+\cdots+k_{n-r} \xi_{n-\mathrm{r}}+\boldsymbol{\eta}^*\left(k_1, k_2, \cdots k_{n-r} \text { 是任意常数 }\right) .

主要考点

齐次线性方程组AX=0AX=0

因为齐次线性方程组一定有零解，所以较少讨论他的情况。主要研究的是非零解。

齐次线性方程组有非零解的充要条件是 ⇔r(A)<n \Leftrightarrow r(A)<n 齐次方程其通解为 r(A)=r,ξ1,ξ2,⋯ ,ξn−r\mathrm{r}(\boldsymbol{A})=r, \boldsymbol{\xi}_1, \boldsymbol{\xi}_2, \cdots, \boldsymbol{\xi}_{n-\mathrm{r}}

非齐次线性方程组AX=bAX=b

非齐次线性方程组有非零解的判断

{r(A)=r([A:b])=n 时, 方程组有唯一解 r(A)=r([A:b])<n 时, 方程组有无穷多解 r(A)≠r([A:b]) 时, 方程组无解 \left\{\begin{array}{l} r(\boldsymbol{A})=r([\boldsymbol{A}: \boldsymbol{b}])=n \text { 时, 方程组有唯一解 } \\ r(\boldsymbol{A})=r([\boldsymbol{A}: \boldsymbol{b}])<n \text { 时, 方程组有无穷多解 } \\ r(\boldsymbol{A}) \neq r([\boldsymbol{A}: \boldsymbol{b}]) \text { 时, 方程组无解 } \end{array}\right.

非齐次线性方程组的通解= 齐次线性方程组的通解 + 特解

点击查看齐次方程的解和非齐次方程的解的求法。

同解方程组 (通常是期末考试大题)

{Ax=0,Bx=0 是同解方程组 ⇔Ax=0 的解满足 Bx=0, 且 Bx=0 的解满足 Ax=0⇔r(A)=r(B), 且 Ax=0 的解满足 Bx=0⇔r(A)=r(B)=r([AB])\left\{\begin{aligned} & \boldsymbol{A x}=\mathbf{0}, \boldsymbol{B x}=\mathbf{0} \text { 是同解方程组 } \\ \Leftrightarrow & \boldsymbol{A x}=\mathbf{0} \text { 的解满足 } \boldsymbol{B x}=\mathbf{0}, \text { 且 } \boldsymbol{B x}=\mathbf{0} \text { 的解满足 } \boldsymbol{A x}=\mathbf{0} \\ \Leftrightarrow & r(\boldsymbol{A})=r(\boldsymbol{B}), \text { 且 } \boldsymbol{A x}=\mathbf{0} \text { 的解满足 } \boldsymbol{B x}=\mathbf{0} \\ \Leftrightarrow & r(\boldsymbol{A})=r(\boldsymbol{B})=r\left(\left[\begin{array}{l} \boldsymbol{A} \\ \boldsymbol{B} \end{array}\right]\right) \end{aligned}\right.

公共解 (通常是考研题)

（1）联立方程 [AB]x=0\left[\begin{array}{l}\boldsymbol{A} \\ \boldsymbol{B}\end{array}\right] x=0 的解 （2）求出 Am×nx=0\boldsymbol{A}_{m \times n} \boldsymbol{x}=\mathbf{0} 的通解 k1ξ1+k2ξ2+⋯+ksξsk_1 \xi_1+k_2 \xi_2+\cdots+k_s \xi_s ，代人 Bm×nx=0\boldsymbol{B}_{m \times n} \boldsymbol{x}= \mathbf{0} ，求出 kik_i 之间的关系，代回 Am×nx=0\boldsymbol{A}_{m \times n} \boldsymbol{x}=\mathbf{0} 的通解 （3）给出 Am×nx=0\boldsymbol{A}_{m \times n} \boldsymbol{x}=\mathbf{0} 的基础解系 ξ1,ξ2,⋯ ,ξs\xi_1, \xi_2, \cdots, \xi_s 与 Bm×nx=0\boldsymbol{B}_{m \times n} \boldsymbol{x}=\mathbf{0}的基础解系 η1,η2,⋯ ,ηt\boldsymbol{\eta}_1, \boldsymbol{\eta}_2, \cdots, \boldsymbol{\eta}_t ，则公共解

γ=k1ξ1+k2ξ2+⋯+ksξs=l1η1+l2η2+⋯+l1η1\gamma=k_1 \xi_1+k_2 \xi_2+\cdots+k_s \xi_s=l_1 \eta_1+l_2 \eta_2+\cdots+l_1 \eta_1
前の章4线性方程组的解
次の章2._方程的的解的判定概述