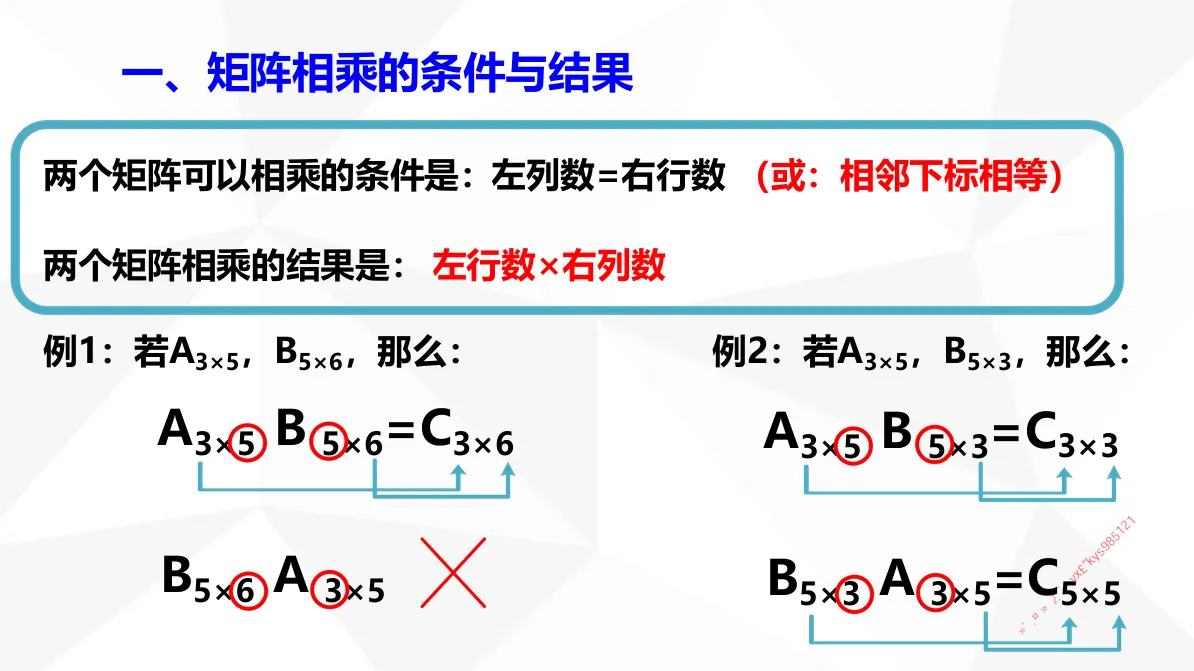
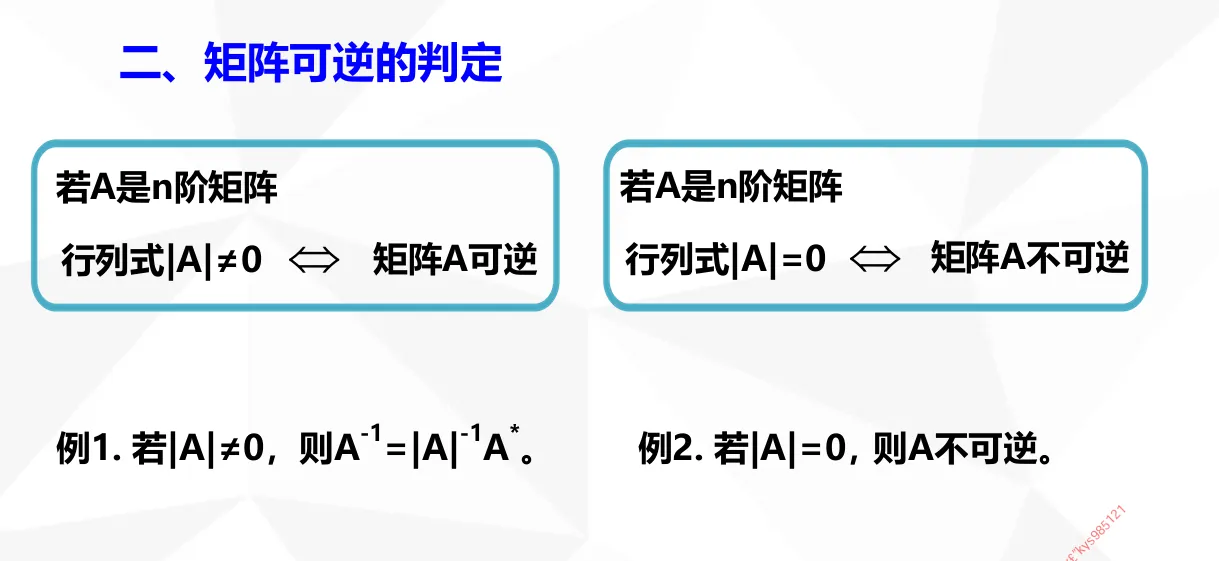
2._方程的的解的判定概述

下面给出本章内容判定方程解的结论，方便日后查找。后续章节将详细要论这些结论。

行列式和方程的解

如果行列式$|A| \ne 0$不等于零，则方程$Ax=0$只有零解。 如果行列式$|A| = 0$等于零，则方程$Ax=0$有非零解。

记忆方法：你不等于零，我等于零。 你等于零，我就不等于零。（总之，我就和你对着干）

如果行列式$|A| \ne 0$不等于零，则方程$Ax=b$ 有唯一解。 如果行列式$|A| = 0$等于零，则方程$Ax=b$ 无解或无穷解。

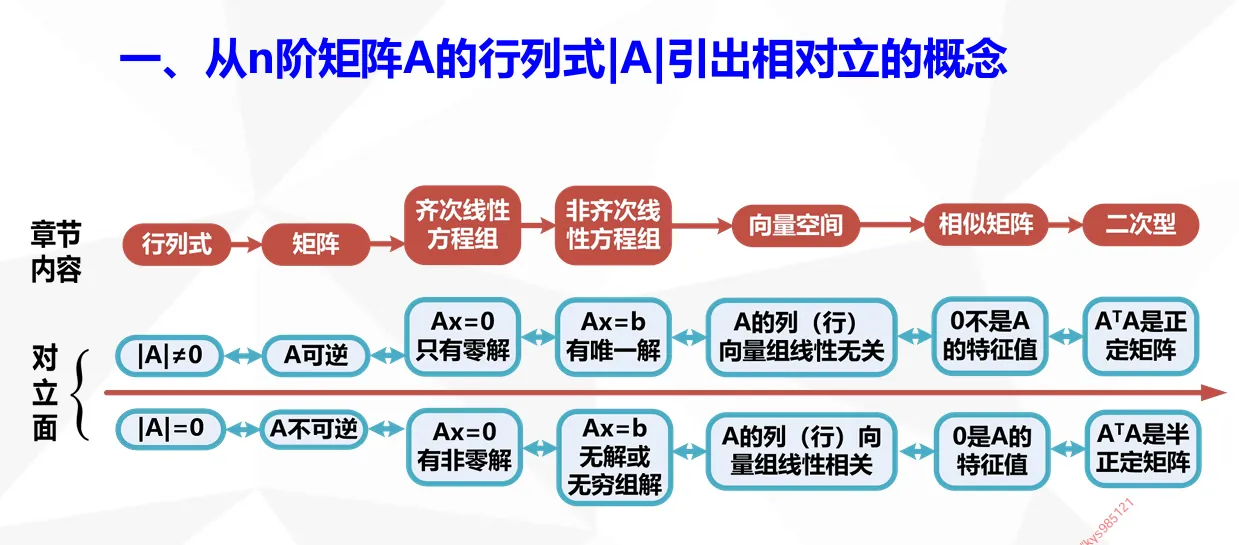
矩阵的秩和方程的解

理解四个默认参数的含义： $n$:方程里未知数的个数 $r$:矩阵的秩，表示方程的个数。 $r_c$:增广矩阵的秩，表示方程的个数。 $n-r$:自由未知数的个数。

记忆方法：秩$r$越大，表示约束条件越强；$n-r$：未被约束的“自由度”。自由度越大，解就越多

{width=500px}

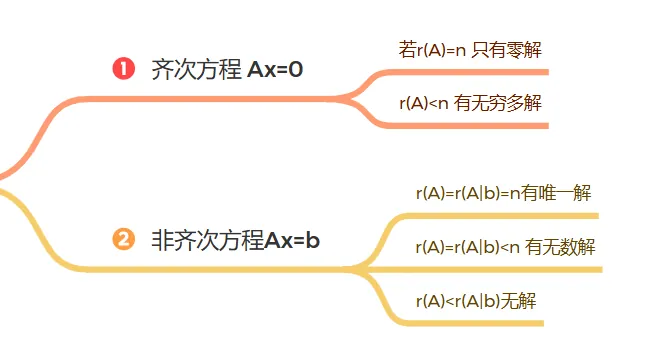{width=500px}

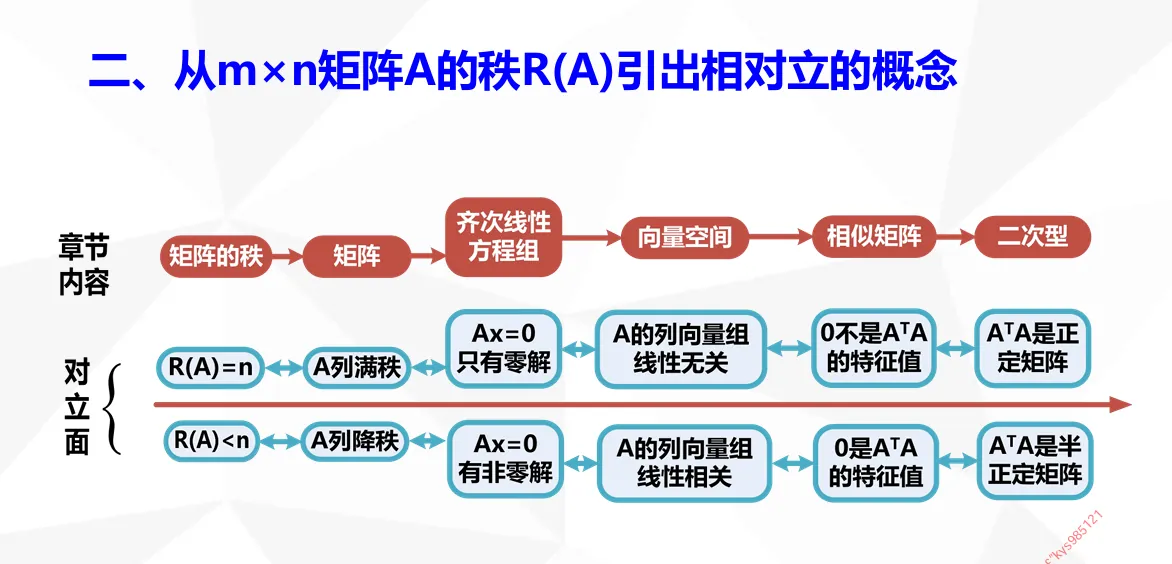
秩的大小与方程解的关系

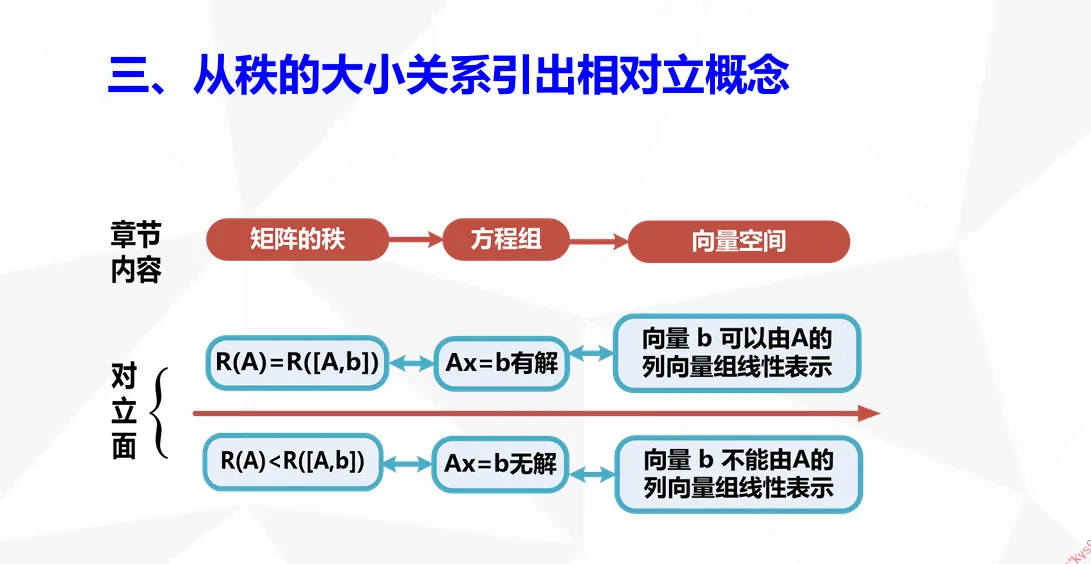
系数矩阵的秩和增广矩阵的秩相等，有解（包括有一个解和无穷多解） 系数矩阵的秩小于增广矩阵的秩，则无解

记忆方法：$r(A) < r(A|b)$：要求太高，能力达不到 -> 无解 $r(A) = r(A|b)$：要求刚刚好，能力刚好 -> 有解 情况①= n：要求非常精确 -> 唯一解 情况②< n：要求比较宽松 -> 无穷多解

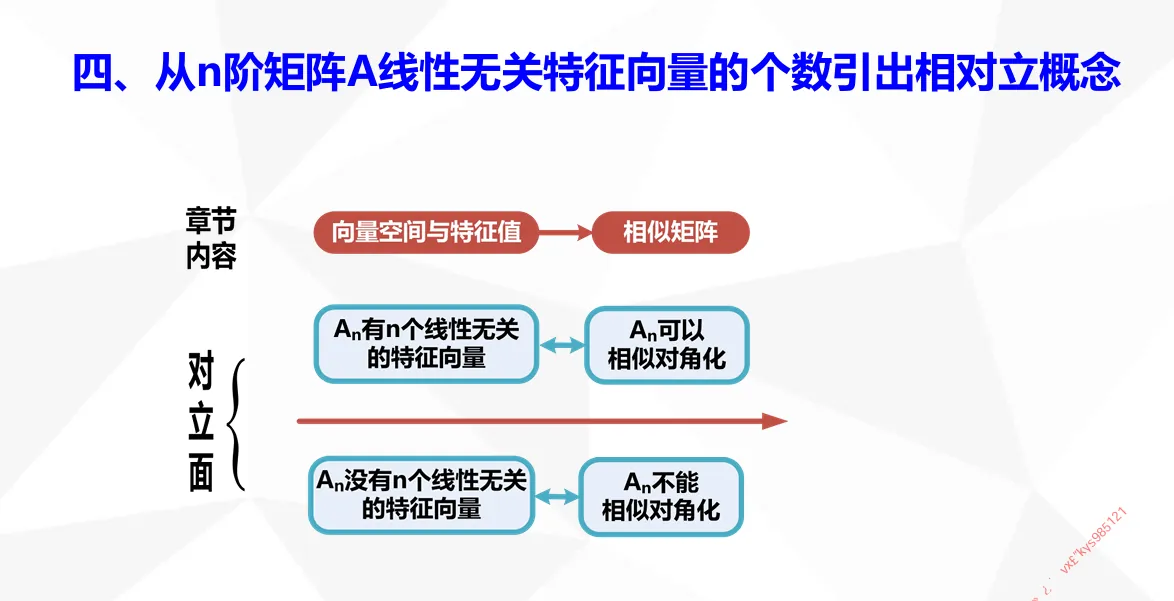
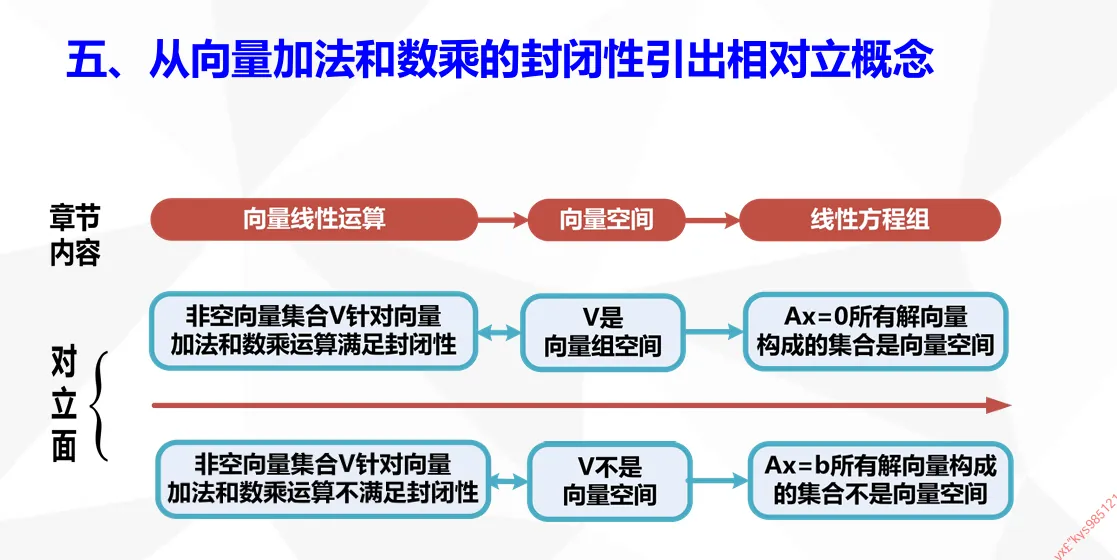
以值判定