6._齐次方程组解的结构_基础解系

齐次方程组的解

齐次方程组一定有零解，所以，他要么有唯一的零解，要么有无穷多解。

① 唯一的零解 从本质上来说，方程组有唯一零件是两个直线斜率不一样，且直线仅在原点相交,对于零解，我们通常不感兴趣，我们更感兴趣的是无穷解。

{x1+x2=02x1+3x2=0⟶{x1=0x2=0\begin{aligned} &\left\{\begin{array} { r } { x _ { 1 } + x _ { 2 } = 0 } \\ { 2 x _ { 1 } + 3 x _ { 2 } = 0 } \end{array} \longrightarrow \left\{\begin{array}{l} x_1=0 \\ x_2=0 \end{array}\right.\right. \end{aligned}

② 无穷多解 从本质上来说，方程组有无穷多解是两个直线重合或平面重合或体积重合等。

{x1+x2=02x1+2x2=0⟶{x1=0x2=0...{x1=1x2=−1\left\{ \begin{array} { r } { x _ { 1 } + x _ { 2 } = 0 } \\ { 2 x _ { 1 } + 2 x _ { 2 } = 0 } \end{array} \longrightarrow \left\{\begin{array} { l } { x _ { 1 } = 0 } \\ { x _ { 2 } = 0 } \end{array}\right. ... \left\{\begin{array}{l} x_1=1 \\ x_2=-1 \end{array}\right. \right.

对于有无穷多解，重点是如何写出他的基础解系。

比如对于上面的方程，可以写成

{x1+x2=02x1+2x2=0⟶x1=kx2=−k\begin{aligned} \left\{\begin{array}{r} x_1+x_2=0 \\ 2 x_1+2 x_2=0 \end{array}\right. & \end{aligned} \longrightarrow \begin{aligned} & x_1=k \\ & x_2=-k \end{aligned}

更进一步的，上面方程的解可以写成向量形式是：

x=[x1x2]=k[1−1]x=\left[\begin{array}{l} x_1 \\ x_2 \end{array}\right]=k\left[\begin{array}{c} 1 \\ -1 \end{array}\right]

此时，虽然这个方程有无穷多解，但是使用上面这个表达式可以表示出这个方程所有的解，我们给这个解一个名称：基础解系

但是，当变量很多时，我们需要一个方法来方便写出他的基础解系，而不能靠猜。

下面通过一个具体的例题介绍齐次线性方程组解的求解套路。只要一道题目会了，整个解法就会了，不过想熟练掌握还是需要大量练习，科数题库提供了海量试题供你训练，点击查看 基础解系训练

齐次线性方程组解基础解系求解套路

例 求齐次线性方程组 {x1+x2+x3−2x5=02x1+2x2+x3+2x4−3x5=0x1+x2+3x3−4x4−4x5=0\left\{\begin{array}{cr}x_1+x_2+x_3 -2 x_5=0 \\ 2 x_1+2 x_2+x_3+2 x_4-3 x_5=0 \\ x_1+x_2+3 x_3-4 x_4-4 x_5=0\end{array}\right. 的基础解系.

解： 第一步：写出系数矩阵。

A=(1110−22212−3113−4−4)\boldsymbol{A}=\left(\begin{array}{ccccc} 1 & 1 & 1 & 0 & -2 \\ 2 & 2 & 1 & 2 & -3 \\ 1 & 1 & 3 & -4 & -4 \end{array}\right)

第二步： 对系数矩阵 A\boldsymbol{A} 实施初等行变换，化为行最简形矩阵 RR : 行最简形矩阵教程

A=(1110−22212−3113−4−4)→(1110−200−121002−4−2)→(1102−1001−2−100000)=R,\boldsymbol{A}=\left(\begin{array}{ccccc} 1 & 1 & 1 & 0 & -2 \\ 2 & 2 & 1 & 2 & -3 \\ 1 & 1 & 3 & -4 & -4 \end{array}\right) \rightarrow\left(\begin{array}{ccccc} 1 & 1 & 1 & 0 & -2 \\ 0 & 0 & -1 & 2 & 1 \\ 0 & 0 & 2 & -4 & -2 \end{array}\right) \rightarrow\left(\begin{array}{ccccc} 1 & 1 & 0 & 2 & -1 \\ 0 & 0 & 1 & -2 & -1 \\ 0 & 0 & 0 & 0 & 0 \end{array}\right)=\boldsymbol{R},

第三步：写出自由未知量。

由于 R(A)=2<5R(\boldsymbol{A})=2<5 ，所以该齐次线性方程组有非零解.

R\boldsymbol{R} 对应的方程组为（这一步考试时可以不写）:

{x1+x2+2x4−x5=0,x3−2x4−x5=0.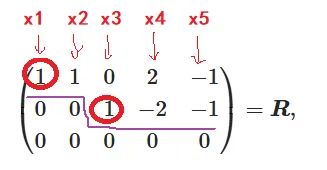\quad\left\{\begin{array}{l}x_1+x_2+2 x_4-x_5=0, \\ x_3-2 x_4-x_5=0 .\end{array}\right.

图片

当我们化为阶梯形最简形后，每行取数字1所在的列为未知量，其它的作为自由未知量。参考上图，行最简形矩阵 R\boldsymbol{R} 的首元在第 1 列和第 3 列，所以使用x1,x3x_1,x_3作为未知量，而x2,x4,x5x_2, x_4, x_5为自由未知量.

并将自由末知量移至等号右端，有

{x1=−x2−2x4+x5,x3=2x4+x5....(2)\left\{\begin{array}{l}x_1=-x_2-2 x_4+x_5, \\ x_3=2 x_4+x_5 .\end{array}\right. ...(2)

第四步：分别取自由未知量(x2,x4,x5)(x_2,x_4,x_5) 的值 (1,0,0) (0,1,0) （0,0,1) 即

分别取 (x2x4x5)=(100),(010),(001)\left(\begin{array}{l}x_2 \\ x_4 \\ x_5\end{array}\right)=\left(\begin{array}{l}1 \\ 0 \\ 0\end{array}\right),\left(\begin{array}{l}0 \\ 1 \\ 0\end{array}\right),\left(\begin{array}{l}0 \\ 0 \\ 1\end{array}\right) \quad

代入(2)方程，具体的为：

① 取 η1=(x2x4x5)=(100)\eta_1= \left(\begin{array}{l}x_2 \\ x_4 \\ x_5\end{array}\right) =\left(\begin{array}{l}1 \\ 0 \\ 0\end{array}\right) 时, (x1x3)=(−10)\left(\begin{array}{l}x_1 \\ x_3\end{array}\right) = \left(\begin{array}{l}-1 \\ 0\end{array}\right)

② 取 η2=(x2x4x5)=(010)\eta_2=\left(\begin{array}{l}x_2 \\ x_4 \\ x_5\end{array}\right) = \left(\begin{array}{l}0\\ 1 \\ 0\end{array}\right) 时, (x1x3)=(−22)\left(\begin{array}{l}x_1 \\ x_3\end{array}\right) = \left(\begin{array}{l} -2 \\ 2\end{array}\right)

③ 取 η3=(x2x4x5)=(001)\eta_3=\left(\begin{array}{l}x_2 \\ x_4 \\ x_5\end{array}\right) = \left(\begin{array}{l}0\\ 0 \\ 1\end{array}\right) 时 ，(x1x3)=(11)\left(\begin{array}{l}x_1 \\ x_3\end{array}\right) = \left(\begin{array}{l} 1 \\ 1\end{array}\right)

第五步 把η1，η2，η3\eta_1，\eta_2，\eta_3 合并，从而基础解系为:

ξ1=(−11000),ξ2=(−20210),ξ3=(10101)\begin{aligned} &\xi_1=\left(\begin{array}{c} -1 \\ 1 \\ 0 \\ 0 \\ 0 \end{array}\right), \quad \xi_2=\left(\begin{array}{c} -2 \\ 0 \\ 2 \\ 1 \\ 0 \end{array}\right), \quad \xi_3=\left(\begin{array}{l} 1 \\ 0 \\ 1 \\ 0 \\ 1 \end{array}\right) \end{aligned}

第六步 写出通解方程 原方程组的通解为

x=k1ξ1+k2ξ2+k3ξ3.\boldsymbol{x}=k_1 \xi_1 +k_2 \xi_2+k_3 \xi_3 .

带入即可最终结果为：

x=k1(−11000)+k2(−20210)+k3(10101).\boldsymbol{x}=k_1 \left(\begin{array}{c} -1 \\ 1 \\ 0 \\ 0 \\ 0 \end{array}\right) +k_2 \left(\begin{array}{c} -2 \\ 0 \\ 2 \\ 1 \\ 0 \end{array}\right) +k_3 \left(\begin{array}{l} 1 \\ 0 \\ 1 \\ 0 \\ 1 \end{array}\right) .

别忘了再加 k1,k2,k3k_1,k_2,k_3 为任意常数。虽然大家都知道他是任意常数，如果不加这句，有些老师还是会扣你1分。

以上就是求解基础解系固定的常用套路，只要这个套路学会了，再碰到方程组的解的问题，应该就很容易解决了

例题

例 解方程

{x1+x2+2x3−7x4−4x5=02x1+5x2+4x3−2x5=0x1+2x2+2x3−2x4−2x5=0x2+2x4+2x5=0\left\{\begin{array}{l} x_1+x_2+2 x_3-7 x_4-4 x_5=0 \\ 2 x_1+5 x_2+4 x_3-2 x_5=0 \\ x_1+2 x_2+2 x_3-2 x_4-2 x_5=0 \\ x_2+2 x_4+2 x_5=0 \end{array}\right.

解法1：写出系数矩阵

[112−7−42540−2122−2−201022]\left[\begin{array}{ccccc} 1 & 1 & 2 & -7 & -4 \\ 2 & 5 & 4 & 0 & -2 \\ 1 & 2 & 2 & -2 & -2 \\ 0 & 1 & 0 & 2 & 2 \end{array}\right]

把他化为阶梯形矩阵

[1020−6010020001000000]\left[\begin{array}{ccccc} 1 & 0 & 2 & 0 & -6 \\ 0 & 1 & 0 & 0 & 2 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{array}\right]

在阶梯形矩阵里，下图画圈的主未知量，而其它的为自由未知量。 图片

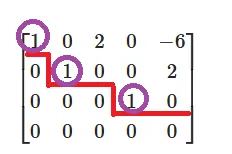
对应方程组为

{x1+2x3−6x5=0x2+2x5=0x4=0\left\{\begin{array}{l} x_1+2 x_3-6 x_5=0 \\ x_2+2 x_5=0 \\ x_4=0 \end{array}\right.

即

{x1=−2x3+6x5x2=−2x5x4=0...(★)\left\{\begin{array}{l} x_1=-2 x_3+6 x_5 \\ x_2=-2 x_5 \\ x_4=0 \end{array}\right. ...(★)

令自由变量 x3=c1,x5=c2(c1,c2∈R)x_3=c_1, x_5=c_2 \quad\left(c_1, c_2 \in R\right)

{x1=−2c1+6c2x2=−2c2x3=c1x4=0x5=c2\left\{\begin{array}{l} x_1=-2 c_1+6 c_2 \\ x_2=-2 c_2 \\ x_3=c_1 \\ x_4=0 \\ x_5=c_2 \end{array}\right.

因此解空间为 (c1,c2c_1,c_2 分别取 (1,0),(0,1)(1,0),(0,1))

(x1x2x3x4x5)=c1(−20100)+c2(6−2001)(c1,c2∈R)\left(\begin{array}{l} x_1 \\ x_2 \\ x_3 \\ x_4 \\ x_5 \end{array}\right)=c_1\left(\begin{array}{c} -2 \\ 0 \\ 1 \\ 0 \\ 0 \end{array}\right)+c_2\left(\begin{array}{c} 6 \\ -2 \\ 0 \\ 0 \\ 1 \end{array}\right) \quad\left(c_1, c_2 \in R\right)

解法2： 根据 (★) 依次令自由变量等于 1 ，其余自由变量等于 0 ，这样得到的一组解向量就是该齐次方程组的基础解系.

这一过程，使用向量进行操作就是分别令自由变量构成的向量等于单位向量的过程。

依次令

(x3x5)=(10),(01)\binom{x_3}{x_5}=\binom{1}{0},\binom{0}{1}

则对应有

(x1x2x4)=(−200),(6−20)\left(\begin{array}{l} x_1 \\ x_2 \\ x_4 \end{array}\right)=\left(\begin{array}{c} -2 \\ 0 \\ 0 \end{array}\right),\left(\begin{array}{c} 6 \\ -2 \\ 0 \end{array}\right)

即得到齐次线性方程组的基础解系

ξ1=(−20100),ξ2=(6−2001)\xi_1=\left(\begin{array}{c} -2 \\ 0 \\ 1 \\ 0 \\ 0 \end{array}\right), \xi_2=\left(\begin{array}{c} 6 \\ -2 \\ 0 \\ 0 \\ 1 \end{array}\right)
x=c1ξ1+c2ξ2(c1,c2∈R)x =c_1 \xi _1+c_2 \xi _2\left(c_1, c_2 \in R\right)

例求齐次线性方程组

{3x1+5x2+6x3−4x4=0,x1+2x2+4x3−3x4=0,4x1+5x2−2x3+3x4=0,3x1+8x2+24x3−19x4=0\left\{\begin{aligned} 3 x_1+5 x_2+6 x_3-4 x_4 & =0, \\ x_1+2 x_2+4 x_3-3 x_4 & =0, \\ 4 x_1+5 x_2-2 x_3+3 x_4 & =0, \\ 3 x_1+8 x_2+24 x_3-19 x_4 & =0 \end{aligned}\right.

的基础解系与通解． 解：首先将系数矩阵化成简化阶梯形矩阵，即

A=(356−4124−345−233824−19)→ 初等行变换 (124−3016−500000000)⟶(10−87016−500000000). A=\left(\begin{array}{rrrr} 3 & 5 & 6 & -4 \\ 1 & 2 & 4 & -3 \\ 4 & 5 & -2 & 3 \\ 3 & 8 & 24 & -19 \end{array}\right) \xrightarrow{\text { 初等行变换 }}\left(\begin{array}{rrrr} 1 & 2 & 4 & -3 \\ 0 & 1 & 6 & -5 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array}\right) \longrightarrow\left(\begin{array}{rrrr} 1 & 0 & -8 & 7 \\ 0 & 1 & 6 & -5 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array}\right) \text {. }

选 x3,x4x_3, x_4 为自由末知量，得基础解系

η1=(8−610),η2=(−7501).\eta _1=\left(\begin{array}{r} 8 \\ -6 \\ 1 \\ 0 \end{array}\right), \quad \eta _2=\left(\begin{array}{r} -7 \\ 5 \\ 0 \\ 1 \end{array}\right) .

于是原方程组的通解为 x=k1η1+k2η2x =k_1 \eta _1+k_2 \eta _2 ，即

x=(x1x2x3x4)=k1(8−610)+k2(−7501),k1,k2 为任意常数. x =\left(\begin{array}{l} x_1 \\ x_2 \\ x_3 \\ x_4 \end{array}\right)=k_1\left(\begin{array}{r} 8 \\ -6 \\ 1 \\ 0 \end{array}\right)+k_2\left(\begin{array}{r} -7 \\ 5 \\ 0 \\ 1 \end{array}\right), k_1, k_2 \text { 为任意常数. }

例 解齐次线性方程组

{−2x1−5x2+8x3−17x5=0,x1+3x2−5x3+x4+5x5=0,3x1+11x2−19x3+7x4+x5=0,x1+7x2−13x3+5x4−3x5=0,\left\{\begin{array}{r} -2 x_1-5 x_2+8 x_3-17 x_5=0, \\ x_1+3 x_2-5 x_3+x_4+5 x_5=0, \\ 3 x_1+11 x_2-19 x_3+7 x_4+x_5=0, \\ x_1+7 x_2-13 x_3+5 x_4-3 x_5=0, \end{array}\right.

且将其通解用基础解系表示。 解 写出系数矩阵 AA ，并作初等行变换化 AA 为行最简形矩阵

A=[−2−580−1713−515311−197117−135−3]→[1010101−2030001−500000]A =\left[\begin{array}{ccccc} -2 & -5 & 8 & 0 & -17 \\ 1 & 3 & -5 & 1 & 5 \\ 3 & 11 & -19 & 7 & 1 \\ 1 & 7 & -13 & 5 & -3 \end{array}\right] \rightarrow\left[\begin{array}{ccccc} 1 & 0 & 1 & 0 & 1 \\ 0 & 1 & -2 & 0 & 3 \\ 0 & 0 & 0 & 1 & -5 \\ 0 & 0 & 0 & 0 & 0 \end{array}\right]

取自由末知量为 x3x_3 和 x5x_5 ，通解为

{x1=−k1−k2,x2=2k1−3k2,x3=k1,x4=5k2,x5=k2,k1,k2 为任意实数. \left\{\begin{array}{l} x_1=-k_1-k_2, \\ x_2=2 k_1-3 k_2, \\ x_3=k_1, \\ x_4=5 k_2, \\ x_5=k_2, \end{array} k_1, k_2\right. \text { 为任意实数. }

写成向量形式为

[x1x2x3x4x5]=k1[−12100]+k2[−1−3051],k1,k2 为任意实数. \left[\begin{array}{l} x_1 \\ x_2 \\ x_3 \\ x_4 \\ x_5 \end{array}\right]=k_1\left[\begin{array}{c} -1 \\ 2 \\ 1 \\ 0 \\ 0 \end{array}\right]+k_2\left[\begin{array}{c} -1 \\ -3 \\ 0 \\ 5 \\ 1 \end{array}\right], k_1, k_2 \text { 为任意实数. }

故基础解系为

X1=(−12100)T,X2=(−1−3051)T,X _1=\left(\begin{array}{lllll} -1 & 2 & 1 & 0 & 0 \end{array}\right)^{T}, \quad X _2=\left(\begin{array}{lllll} -1 & -3 & 0 & 5 & 1 \end{array}\right)^{T},

通解为 k1X1+k2X2k_1 X _1+k_2 X _2 ，其中 k1,k2k_1, k_2 为任意实数．

前の章5._三元齐次线性方程组
次の章7._齐次方程组解的性质
6._齐次方程组解的结构_基础解系 - 线性代数 | OpenTech