9._非齐次线性方程组解的结构_基础解系

非齐次线性方程组的解结构

非齐次方程组解的几何图形是齐次方程组解空间与一个特定常向量 d\boldsymbol{d} 的和,这实际上就是把齐次方程组解空间的几何图形沿着特定向量方向平移了一个距离, 这个距离等于常向量 dd 的长度。

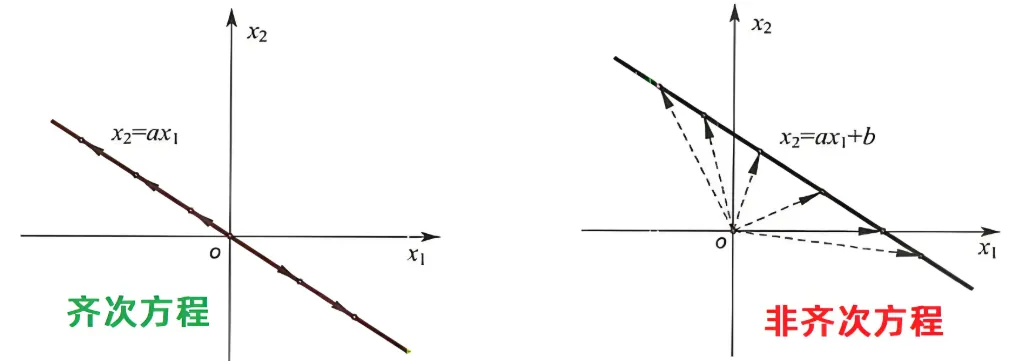
下图显示了x2=ax1x_2=a_x1 和 x2=ax1+bx_2=a_x1+b， 在二维平面上的几何意义。 从图中可以看到，只要我们得到齐次方程的解，再通过平移，即可得到非齐次方程。

图片{width=600px}

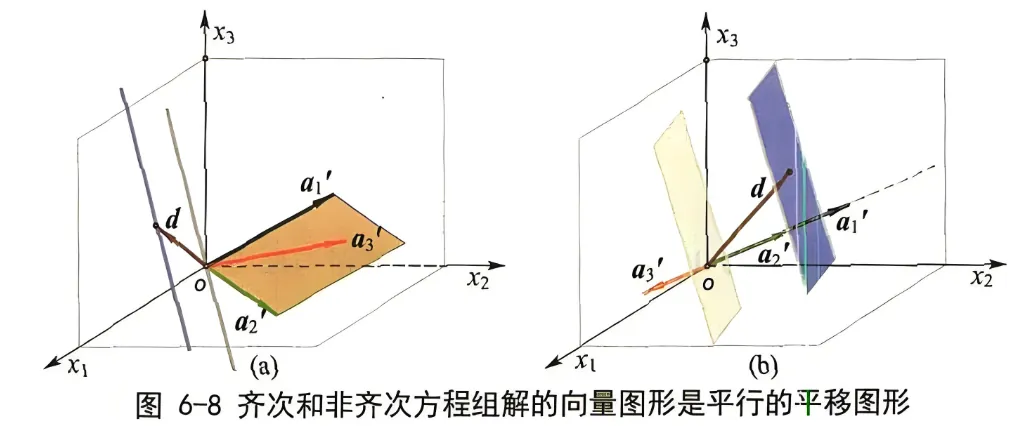
这种思想同样可以应用于三元齐次线性方程组里。如下图，如果解空间是一个直线或者平面, 那么同一个系数矩阵的非齐次线性方程组的解系就是把这根直线或平面平移一个特解向量的距离

图片{width=600px}

结论

所以, 齐次方程组和对应的非齐次方程组的解析几何图形是平行的, 或者说齐次方程组的解的几何图形和对应的非齐次方程组的解的几何图形是平行的。具体来说, 齐次方程组的所谓基础解系 c1ξ1+c2ξ2+⋯+cn−rξn−rc_1 \xi_1+c_2 \xi_2+\cdots+c_{n-r} \xi_{n-r} 的几何图形和非齐次方程组的通解 η+c1ξ1+c2ξ2+⋯+cn−rξn−r\boldsymbol{\eta}+c_1 \xi_1+c_2 \xi_2+\cdots+c_{n-r} \xi_{n-r} 的几何图形是平行的, 基础解系是过原点的超平面, 通解是不过原点 (移开原点) 的平行平面。

值得注意的是, 齐次解的向量图形只要加上任意一个顶点在非齐次图形上的常向量, 就可以得到所有的非齐次解向量, 非齐次解向量的顶点构成了非齐次解的几何图形。

还有一个值得注意的是, 虽然非齐次解向量图形与行向量空间不再正交, 但是非齐次解的几何图形仍然与行空间的几何图形保持垂直的解析性质 (见图 6-8)。

通过上面分析，最终结论就是：

非齐次方程组的通解=对应的齐次方程组的通解+非齐次方程组的一个特解

非齐次线性方程组求解套路

下面通过一个例题介绍非齐次线性方程组基础解系的求法。要参考齐次线性方程组的解系做法，请点击齐次线性方程组解的结构

例 设非齐次线性方程组

{x1+5x2−x3−x4=−1x1−2x2+x3+3x4=33x1+8x2−x3+x4=1x1−9x2+3x3+7x4=7\left\{\begin{array}{c} x_1+5 x_2-x_3-x_4=-1 \\ x_1-2 x_2+x_3+3 x_4=3 \\ 3 x_1+8 x_2-x_3+x_4=1 \\ x_1-9 x_2+3 x_3+7 x_4=7 \end{array}\right.

求其通解。

解：第一步：对增广矩阵化为行最简阶梯形 对所给方程组的增广矩阵 Aˉ\bar{A} 施以初等行变换,化为行简化阶梯形

Aˉ=[15−1−1−11−213338−1111−9377]→[15−1−1−10−72440−72440−14488]→[15−1−1−10−72440000000000]→[103713713701−27−47−470000000000].\begin{aligned} \bar{A} & =\left[\begin{array}{rrrr:r} 1 & 5 & -1 & -1 & -1 \\ 1 & -2 & 1 & 3 & 3 \\ 3 & 8 & -1 & 1 & 1 \\ 1 & -9 & 3 & 7 & 7 \end{array}\right] \rightarrow\left[\begin{array}{rrrr:r} 1 & 5 & -1 & -1 & -1 \\ 0 & -7 & 2 & 4 & 4 \\ 0 & -7 & 2 & 4 & 4 \\ 0 & -14 & 4 & 8 & 8 \end{array}\right] \\ & \rightarrow\left[\begin{array}{rrrr:r} 1 & 5 & -1 & -1 & -1 \\ 0 & -7 & 2 & 4 & 4 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{array}\right] \rightarrow\left[\begin{array}{rrrr:r} 1 & 0 & \frac{3}{7} & \frac{13}{7} & \frac{13}{7} \\ 0 & 1 & -\frac{2}{7} & -\frac{4}{7} & -\frac{4}{7} \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{array}\right] . \end{aligned}

第二步 写出自由未知量，并令自由未知量为0

从最简形选取每行1所在的列作为未知量，其余为自由未知量。参考下图 图片

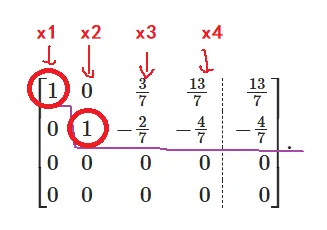
所以，从最简形可以看到，非零行首非零元为x1,x2x_1,x_2, 所以令 x1,x2x_1,x_2 为未知量，而令x3,x4x_3,x_4为自由未知量，由此可得原方程组一般解为

{x1=137−37x3−137x4x2=−47+27x3+47x4...(5)\left\{\begin{array}{l} x_1=\frac{13}{7}-\frac{3}{7} x_3-\frac{13}{7} x_4 \\ x_2=-\frac{4}{7}+\frac{2}{7} x_3+\frac{4}{7} x_4 \end{array}\right. ...(5)

要找到特解，理论上 自由未知量 x3,x4x_3,x_4 取任何值都可以，但是为了方便，我们默认总是取 x3,x4x_3,x_4为0，这样方便计算。

令 x3=x4=0x_3=x_4=0, 得原方程组的一个特解

α0=[137−4700]\alpha_0=\left[\begin{array}{r} \frac{13}{7} \\ -\frac{4}{7} \\ 0 \\ 0 \end{array}\right]

在求特解时，一般令x3=0,x4=0x_3=0,x_4=0 这样最容易计算。 而求通解时，一般令x3=1,x4=0x_3=1,x_4=0 和 x3=0,x4=1x_3=0,x_4=1 请别搞混淆了。

第三步 写出通解方程组基础解系

又因原方程组(5)的导出组的一般解为(也就是去掉常数项的方程)

{x1=−37x3−137x4x2=27x3+47x4\left\{\begin{array}{l} x_1=-\frac{3}{7} x_3-\frac{13}{7} x_4 \\ x_2=\frac{2}{7} x_3+\frac{4}{7} x_4 \end{array}\right.

其中 x3,x4x_3, x_4 为自由未知量. 令自由末知量 x3,x4x_3, x_4 分别取值为

[x3x4]=[10],[01]\left[\begin{array}{l} x_3 \\ x_4 \end{array}\right]=\left[\begin{array}{l} 1 \\ 0 \end{array}\right],\left[\begin{array}{l} 0 \\ 1 \end{array}\right]

可得导出组的一个基础解系为

η1=[−372710],η2=[−1374701]\eta_1=\left[\begin{array}{r} -\frac{3}{7} \\ \frac{2}{7} \\ 1 \\ 0 \end{array}\right], \eta_2=\left[\begin{array}{r} -\frac{13}{7} \\ \frac{4}{7} \\ 0 \\ 1 \end{array}\right]

第四步 解出基础解系 于是原方程组通解为

η=α0+c1η1+c2η2=[137−4700]+c1[−372710]+c2[−1374701],\begin{aligned} \eta & =\alpha_0+c_1 \eta_1+c_2 \eta_2 \\ & =\left[\begin{array}{r} \frac{13}{7} \\ -\frac{4}{7} \\ 0 \\ 0 \end{array}\right]+c_1\left[\begin{array}{r} -\frac{3}{7} \\ \frac{2}{7} \\ 1 \\ 0 \end{array}\right]+c_2\left[\begin{array}{r} -\frac{13}{7} \\ \frac{4}{7} \\ 0 \\ 1 \end{array}\right], \end{aligned}

其中 c1,c2c_1, c_2 为任意常数.

以上就是求解非齐次线性方程组的固定套路。

例题

例 求解下列线性方程组．

{x1+x2+2x3−7x4−4x5=102x1+5x2+4x3−2x5=−2x1+2x2+2x3−2x4−2x5=2x2+2x4+2x5=−2\left\{\begin{array}{l} x_1+x_2+2 x_3-7 x_4-4 x_5=10 \\ 2 x_1+5 x_2+4 x_3-2 x_5=-2 \\ x_1+2 x_2+2 x_3-2 x_4-2 x_5=2 \\ x_2+2 x_4+2 x_5=-2 \end{array}\right.

解：STEP1 使用初等行变换将非齐次线性方程组 Ax=bA x = b 的增广矩阵 B=(A,b)B =( A , b ) 化为行阶梯形矩阵 BrefB_{ref} 。

B=(A,b)∼(112−7−4102540−2−2122−2−2201022−2)∼(112−7−41001022−200010−2000000)=Bref\begin{aligned} B & =( A , b) \\ & \sim \left(\begin{array}{cccccc} 1 & 1 & 2 & -7 & -4 & 10 \\ 2 & 5 & 4 & 0 & -2 & -2 \\ 1 & 2 & 2 & -2 & -2 & 2 \\ 0 & 1 & 0 & 2 & 2 & -2 \end{array}\right) \\ & \sim\left(\begin{array}{cccccc} 1 & 1 & 2 & -7 & -4 & 10 \\ 0 & 1 & 0 & 2 & 2 & -2 \\ 0 & 0 & 0 & 1 & 0 & -2 \\ 0 & 0 & 0 & 0 & 0 & 0 \end{array}\right) \\ & = B _{r e f} \end{aligned}

STEP2 根据行阶梯形矩阵 BrefB _{r e f} 判定非齐次线性方程组解的情况。 如果非齐次线性方程组无解，计算终止；有解，进入下一步．

由 BrefB _{r e f} 可知

R(A)=R(B)=3< 未知数的个数 R( A )=R( B )=3<\text { 未知数的个数 }

方程组有无穷多解．

STEP3 使用初等行变换将行阶梯形矩阵 BrefB _{r e f} 化为行最简形矩阵 BrrefB _{r r e f} ；

Bref =(112−7−41001022−200010−2000000)∼r(1020−6−601002200010−2000000)=Brref \begin{aligned} B _{\text {ref }} & =\left(\begin{array}{cccccc} 1 & 1 & 2 & -7 & -4 & 10 \\ 0 & 1 & 0 & 2 & 2 & -2 \\ 0 & 0 & 0 & 1 & 0 & -2 \\ 0 & 0 & 0 & 0 & 0 & 0 \end{array}\right) \\ & \stackrel{r}{\sim}\left(\begin{array}{cccccc} 1 & 0 & 2 & 0 & -6 & -6 \\ 0 & 1 & 0 & 0 & 2 & 2 \\ 0 & 0 & 0 & 1 & 0 & -2 \\ 0 & 0 & 0 & 0 & 0 & 0 \end{array}\right) \\ & = B _{\text {rref }} \end{aligned}

根据行最简形矩阵 Brref B _{\text {rref }} 确定首变量和自由变量；

首变量为 x1,x2,x4x_1, x_2, x_4 ，自由变量为 x3,x5x_3, x_5 ．

写出行最简形矩阵 BrrefB _{r r e f} 所对应的已知方程组的同解方程组 (⋆)( \star ) ；

{x1+2x3−6x5=−6x2+2x5=2x4=−2...(⋆)\left\{\begin{array}{l} x_1+2 x_3-6 x_5=-6 \\ x_2+2 x_5=2 \\ x_4=-2 \end{array}\right. ...(\star)

将方程组（ ⋆\star ）改写为使用自由变量和常数项表示首变量的形式（ ⋆⋆\star \star ）．

{x1=−2x3+6x5−6x2=−2x5+2x4=−2(⋆⋆)\left\{\begin{array}{l} x_1=-2 x_3+6 x_5-6 \\ x_2=-2 x_5+2 \\ x_4=-2 \end{array}(\star \star)\right.

令自由变量为任意实数，得到方程组的通解．

令

x3=c1,x5=c2(c1,c2∈R){x1=−2c1+6c2−6x2=−2c2+2x3=c1x4=−2x5=c2\begin{aligned} x_3= & c_1, x_5=c_2 \quad\left(c_1, c_2 \in R\right) \\ & \left\{\begin{array}{l} x_1=-2 c_1+6 c_2-6 \\ x_2=-2 c_2+2 \\ x_3=c_1 \\ x_4=-2 \\ x_5=c_2 \end{array}\right. \end{aligned}

亦即

x=(x1x2x3x4x5)=c1(−20100)+c2(6−2001)+(−620−20)c1,c2∈Rx =\left(\begin{array}{l} x_1 \\ x_2 \\ x_3 \\ x_4 \\ x_5 \end{array}\right)=c_1\left(\begin{array}{c} -2 \\ 0 \\ 1 \\ 0 \\ 0 \end{array}\right)+c_2\left(\begin{array}{c} 6 \\ -2 \\ 0 \\ 0 \\ 1 \end{array}\right)+\left(\begin{array}{c} -6 \\ 2 \\ 0 \\ -2 \\ 0 \end{array}\right) \quad c_1, c_2 \in R

例 求解线性方程组

{x1−2x2−x3+2x4=4,2x1−2x2−3x3=2,4x1−2x2−7x3−4x4=−2.\left\{\begin{aligned} x_1-2 x_2-x_3+2 x_4 & =4, \\ 2 x_1-2 x_2-3 x_3 & =2, \\ 4 x_1-2 x_2-7 x_3-4 x_4 & =-2 . \end{aligned}\right.

解 写出增广矩阵，并利用初等行变换进行化简：

A‾=[1−2−1242−2−3024−2−7−4−2]→[1−2−12402−1−4−606−3−12−18]\overline{ A }=\left[\begin{array}{cccc|c} 1 & -2 & -1 & 2 & 4 \\ 2 & -2 & -3 & 0 & 2 \\ 4 & -2 & -7 & -4 & -2 \end{array}\right] \rightarrow\left[\begin{array}{cccc|c} 1 & -2 & -1 & 2 & 4 \\ 0 & 2 & -1 & -4 & -6 \\ 0 & 6 & -3 & -12 & -18 \end{array}\right]
→[1−2−12402−1−4−600000]→[10−2−2−201−12−2−300000]\rightarrow\left[\begin{array}{cccc|c} 1 & -2 & -1 & 2 & 4 \\ 0 & 2 & -1 & -4 & -6 \\ 0 & 0 & 0 & 0 & 0 \end{array}\right] \rightarrow\left[\begin{array}{cccc|c} 1 & 0 & -2 & -2 & -2 \\ 0 & 1 & -\frac{1}{2} & -2 & -3 \\ 0 & 0 & 0 & 0 & 0 \end{array}\right]

原方程组有解。其同解方程组为

{x1−2x3−2x4=−2x2−12x3−2x4=−3\left\{\begin{aligned} x_1 \quad-2 x_3-2 x_4 & =-2 \\ x_2-\frac{1}{2} x_3-2 x_4 & =-3 \end{aligned}\right.

取 x3,x4x_3, x_4 为自由变量，方程组的通解为

[x1x2x3x4]=[2x3+2x4−212x3+2x4−3x3x4]=[−2−300]+k1[21210]+k2[2201],\left[\begin{array}{c} x_1 \\ x_2 \\ x_3 \\ x_4 \end{array}\right]=\left[\begin{array}{c} 2 x_3+2 x_4-2 \\ \frac{1}{2} x_3+2 x_4-3 \\ x_3 \\ x_4 \end{array}\right]=\left[\begin{array}{c} -2 \\ -3 \\ 0 \\ 0 \end{array}\right]+k_1\left[\begin{array}{l} 2 \\ \frac{1}{2} \\ 1 \\ 0 \end{array}\right]+k_2\left[\begin{array}{l} 2 \\ 2 \\ 0 \\ 1 \end{array}\right],

其中 k1,k2k_1, k_2 是任意实数．

例 已知 γ1,γ2,γ3\gamma_1, \gamma_2, \gamma_3 是三元非齐次线性方程组 Ax=βA x=\beta 的解， r(A)=1r( A )=1 ，且

γ1+γ2=(100),γ2+γ3=(110),γ1+γ3=(111)\gamma_1+\gamma_2=\left(\begin{array}{l} 1 \\ 0 \\ 0 \end{array}\right), \gamma_2+\gamma_3=\left(\begin{array}{l} 1 \\ 1 \\ 0 \end{array}\right), \gamma_1+\gamma_3=\left(\begin{array}{l} 1 \\ 1 \\ 1 \end{array}\right)

求方程组 Ax=βA x=\beta 的通解． 解：令

η1=(γ2+γ3)−(γ1+γ2)=(010),η2=(γ1+γ3)−(γ2+γ3)=(001),\begin{aligned} & \eta _1=\left(\gamma_2+\gamma_3\right)-\left(\gamma_1+\gamma_2\right)=\left(\begin{array}{l} 0 \\ 1 \\ 0 \end{array}\right), \\ & \eta _2=\left(\gamma_1+\gamma_3\right)-\left(\gamma_2+\gamma_3\right)=\left(\begin{array}{l} 0 \\ 0 \\ 1 \end{array}\right), \end{aligned}

由非齐次线性方程组解的性质与解的结构可知， η1,η2\eta _1, \eta _2 是对应的齐次线性方程组的基础解系，12(γ1+γ2)=(1200)\frac{1}{2}\left( \gamma _1+ \gamma _2\right)=\left(\begin{array}{c}\frac{1}{2} \\ 0 \\ 0\end{array}\right) 是非齐次线性方程组的一个特解．因而，原方程组的通解为

x=12(γ1+γ2)+k1η1+k2η2=(1200)+k1(010)+k2(001)x =\frac{1}{2}\left( \gamma _1+ \gamma _2\right)+k_1 \eta _1+k_2 \eta _2=\left(\begin{array}{c} \frac{1}{2} \\ 0 \\ 0 \end{array}\right)+k_1\left(\begin{array}{l} 0 \\ 1 \\ 0 \end{array}\right)+k_2\left(\begin{array}{l} 0 \\ 0 \\ 1 \end{array}\right)

其中 k1,k2k_1, k_2 是任意常数．

前の章8._三元非齐次线性方程组
次の章10._非齐次方程解的性质