2._数学空间与欧氏空间

线性空间理论主要研究向量间的线性关系，前面介绍了向量的性质，单我们还关心向量的度量性质：向量的长度、距离和夹角等。我们也可用类比方法把这些几何概念移植到一般的线性空间中来，从而得到一类具有度量性质的线性空间——内积空间．实数域上的内积空间叫作欧几里得（Euclid）空间，简称欧氏空间．本节简要介绍欧氏空间的基本概念和基本性质．

近世代数对数学的整体思考(简版)

参考下图:一个个数字或者物体被称作元素，元素放在一起组成了集合(这个高中就学过)，集合排在一起组成了空间，如果空间满足八大性质(交换律、结合律等)则被定义为线性空间。空间里元素的距离称为度量空间。我们需要一个尺子作为度量的基准，这个尺子被称为范数，含有范数的空间称为线性赋范空间，具备完备后称为巴拿赫空间。详见序言 近世代数对数学的整体思考

图片

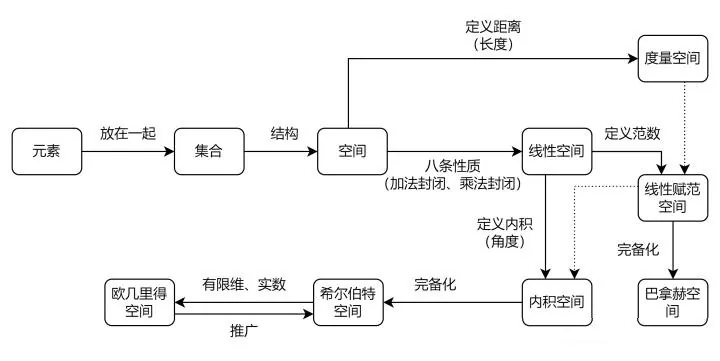
这里要强调一下封闭性，如果集合FF里的数进行加减乘除仍在FF里，则FF称为封闭数域，比如“全体有理数”就是一个封闭数域，因为任何有理数的加减乘除仍在有理数里，但是“全体整数”就不是封闭数域，因为两个数相除有可能是分数。由空间的封闭圈可以引入群的概念。

线性空间的一些关系表 图片

数学空间的思考

数学中的“空间”是一个核心且丰富的概念，它远不止我们日常生活中理解的三维物理空间。数学家通过定义不同的“空间”，来为各种数学对象（如点、函数、序列等）提供一个具有特定结构和规则的“舞台”，以便系统地研究它们的性质。

下面我将从最直观的开始，逐步深入到更抽象的空间，为您梳理一个清晰的脉络。

一、核心思想：从具体到抽象

数学空间的发展史就是一个不断抽象化和一般化的过程。其核心是在集合的基础上，逐步添加“结构”或“规则”。

  1. 集合：最基础，只是一堆元素的汇集，没有其他任何规则。

  2. + 拓扑：添加了“邻近性”或“收敛性”的概念（比如“无限接近”某个点），得到拓扑空间。

  3. + 度量：添加了“距离”的概念，可以精确衡量两点远近，得到度量空间。

  4. + 线性：添加了“加法和数乘”的代数结构，元素之间可以线性组合，得到向量空间（线性空间）。

  5. + 内积：添加了“角度和长度”的概念，可以定义正交性和投影，得到内积空间。

很多常见的空间都是上述结构的组合。下图清晰地展示了这些核心空间之间的层次与演进关系：

图片{width=1000px}

二、详细空间介绍

让我们沿着上图的脉络，详细了解这些重要的空间。

1. 欧氏空间

  • 描述：最直观和熟悉的空间，即我们通常所说的二维平面、三维空间的高维推广。它是有限维的实内积空间。

  • 核心结构：

  1. 向量空间：元素是向量，可以进行加法和数乘（标量乘法）。

  2. 内积：定义了内积（点积）<u, v>，从而可以计算长度（范数 ||u|| = √<u,u>）和夹角（cosθ = <u, v> / (||u|| ||v||)）。

  • 例子：R², R³, Rⁿ（n维实数向量空间）。

2. 酉空间

  • 描述：欧氏空间在复数域上的推广，是有限维的复内积空间。

  • 核心结构：与欧氏空间类似，但所有标量都是复数，并且内积的定义需要满足共轭对称性（<u, v> = conjugate(<v, u>)），以保证向量的长度（范数）是实数。

  • 应用：量子力学的数学基础。量子系统的状态向量就存在于一个酉空间（希尔伯特空间）中。

3. 希尔伯特空间

  • 描述：完备的内积空间。它可以看作是“无限维的欧氏/酉空间”。

  • “完备”意味着空间中的柯西序列都收敛于空间内的一个点（没有“ holes”）。

  • 元素可以是无限维的向量、函数等。

  • 核心结构：内积 + 完备性。

  • 例子：

  • 所有满足 ∫|f(x)|² dx < ∞ 的函数构成的空间（L² 空间）。

  • 所有平方可和的无限序列构成的空间（l² 空间）。

  • 应用：泛函分析、量子力学、傅里叶分析的核心舞台。

4. 赋范空间 与 巴拿赫空间

  • 赋范空间：定义了范数（长度）||·|| 的向量空间。它**不一定有内积（角度）**的概念。所有内积空间都是赋范空间（因为内积可以诱导出范数），但反过来不一定成立。

  • 巴拿赫空间：完备的赋范空间。

  • 例子：

  • 欧氏空间 Rⁿ：既是希尔伯特空间，也是巴拿赫空间。

  • Lᵖ 空间 (p ≠ 2)：定义了范数 ||f||_p = (∫|f(x)|ᵖ dx)^(1/p) 的函数空间，是巴拿赫空间但不是希尔伯特空间（因为其范数不能由内积诱导）。

  • 所有连续函数在上确界范数 ||f||_∞ = sup|f(x)| 下构成的空间。

5. 度量空间

  • 描述：定义了距离函数 d(x, y) 的集合。这是“远近”概念的最一般化。

  • 核心结构：距离（满足正定性、对称性、三角不等式）。

  • 关系：任何赋范空间都可以自然诱导出一个度量空间（定义 d(x, y) = ||x - y||）。但有度量不一定有线性结构（比如一个曲面本身可以作为度量空间）。

  • 例子：

  • 任何赋范空间。

  • 具有通常欧氏距离的 Rⁿ。

  • 一个曲面（如球面）配上测地线距离。

6. 拓扑空间

  • 描述：最一般、最基础的“空间”概念。它只关心“邻近性”和“连续性”，而不再有“距离”这种精确度量。

  • 核心结构：开集（或等价地，闭集、邻域等）。开集族定义了拓扑。

  • 关系：任何度量空间都可以自然诱导出一个拓扑空间（以开球为基）。但存在非常奇怪的拓扑空间无法用任何度量诱导出来（非度量化拓扑空间）。

  • 应用：是现代数学许多分支（如微分几何、代数拓扑）的基础语言。

三、其他重要的空间

除了上述主线，还有许多在特定领域极其重要的空间：

  • 流形：局部类似欧氏空间的拓扑空间。例如，球面、环面在局部看起来都像是一个平面（二维流形）。光滑流形上可以做微积分，这是微分几何的研究对象。

  • 黎曼流形：配备了黎曼度量的微分流形，在每一点都有一个内积，从而可以计算长度、角度、曲率等。它是广义相对论的时空模型。

  • 函数空间：元素是函数的向量空间。例如，所有连续函数 C([a,b])、平方可积函数 L²、光滑函数等。它们是泛函分析和研究微分方程的解空间的核心。

  • 样本空间：概率论中的基础概念，是一个集合，包含所有可能的随机试验结果。

  • 仿射空间：没有“原点”概念的几何空间。只有点、直线和平行等概念，不能像向量空间那样直接做向量的加法。欧氏几何其实是在仿射空间中进行的。

  • 射影空间：由仿射空间添加“无穷远点”而得到，在透视几何、代数几何和计算机图形学中非常重要。

总结来说，数学中的空间是一个层次分明、不断抽象的庞大体系。从具体的欧氏空间和酉空间出发，通过添加或削弱不同的公理（距离、长度、角度、线性结构、完备性、邻近性），数学家们构建出了各种各样的空间，以适应不同数学对象和研究方向的需要。

欧氏空间的定义

定义 设 VV 为实数域 R\mathbb{R} 上的一个线性空间．对 VV 中的任意一对元素 α\boldsymbol{\alpha} 与 β\boldsymbol{\beta} ，都有 R\mathbb{R} 中唯一的一个实数与之对应，将此实数记作 (α,β)(\boldsymbol{\alpha}, \boldsymbol{\beta}) ，若此对应关系满足以下条件： （1）对称性：(α,β)=(β,α),∀α,β∈V(\boldsymbol{\alpha}, \boldsymbol{\beta})=(\boldsymbol{\beta}, \boldsymbol{\alpha}), \forall \boldsymbol{\alpha}, \boldsymbol{\beta} \in V ； （2）线性性：(kα+lβ,γ)=k(α,γ)+l(β,γ),∀k,l∈R(k \boldsymbol{\alpha}+l \boldsymbol{\beta}, \boldsymbol{\gamma})=k(\boldsymbol{\alpha}, \boldsymbol{\gamma})+l(\boldsymbol{\beta}, \boldsymbol{\gamma}), \forall k, l \in \mathbb{R} ， α,β,γ∈V\boldsymbol{\alpha}, \boldsymbol{\beta}, \boldsymbol{\gamma} \in V ； （3）正定性：(α,α)⩾0(\boldsymbol{\alpha}, \boldsymbol{\alpha}) \geqslant 0 且 (α,α)=0(\boldsymbol{\alpha}, \boldsymbol{\alpha})=0 的充分必要条件是 α=0\boldsymbol{\alpha}=\mathbf{0} ，则称 (α,β)(\boldsymbol{\alpha}, \boldsymbol{\beta}) 为向量 α\boldsymbol{\alpha} 与 β\boldsymbol{\beta} 的内积，定义了内积的实线性空间 VV称之为一个欧几里得空间，简称欧氏空间．

长度

设 VV 为欧氏空间，对 VV 中任意向量 α\boldsymbol{\alpha} ，令

∣α∣=(α,α),|\boldsymbol{\alpha}|=\sqrt{(\boldsymbol{\alpha}, \boldsymbol{\alpha})},

称 ∣α∣|\boldsymbol{\alpha}| 为向量 α\boldsymbol{\alpha} 的长度．

若 ∣α∣=1|\boldsymbol{\alpha}|=1 ，则称 α\boldsymbol{\alpha} 为单位向量．

另一方面，若 β\boldsymbol{\beta} 是 VV 中的任一非零向量，令

β0=1∣β∣β,\beta^0=\frac{1}{|\beta|} \beta,

那么 β0\boldsymbol{\beta}^0 是单位向量，构造 β0\boldsymbol{\beta}^0 的方法常称为向量的单位化． 关于欧氏空间的长度，有以下定理．

定理

设 VV 为欧氏空间， α,β∈V,k∈R\boldsymbol{\alpha}, \boldsymbol{\beta} \in V, k \in \mathbb{R} ，则 （1）∣α∣⩾0|\boldsymbol{\alpha}| \geqslant 0 ，且 ∣α∣=0|\boldsymbol{\alpha}|=0 的充分必要条件是 α=0\boldsymbol{\alpha}=\mathbf{0} ； （2）∣kα∣=∣k∣⋅∣α∣,∀k∈K,α∈V|k \boldsymbol{\alpha}|=|k| \cdot|\boldsymbol{\alpha}|, \quad \forall k \in K, \boldsymbol{\alpha} \in V ； （3）［柯西－施瓦茨（Cauchy－Schwarz）不等式］∣(α,β)∣⩽∣α∣⋅∣β∣,∀α,β∈V|(\boldsymbol{\alpha}, \boldsymbol{\beta})| \leqslant |\boldsymbol{\alpha}| \cdot|\boldsymbol{\beta}|, \forall \boldsymbol{\alpha}, \boldsymbol{\beta} \in V ，当且仅当 α\boldsymbol{\alpha} 与 β\boldsymbol{\beta} 线性相关时， ∣(α,β)∣=∣α∣⋅∣β∣|(\boldsymbol{\alpha}, \boldsymbol{\beta})|=|\boldsymbol{\alpha}| \cdot|\boldsymbol{\beta}|.

证明：（1）与（2）显然．今证（3），若 α\boldsymbol{\alpha} 与 β\boldsymbol{\beta} 线性相关，则 α\boldsymbol{\alpha}与 β\boldsymbol{\beta} 共线，不妨设 β=kα\boldsymbol{\beta}=k \boldsymbol{\alpha} ，于是

∣(α,β)∣=∣(α,kα)∣=∣k∣⋅∣(α,α)∣=∣k∣⋅∣α∣2=∣α∣⋅∣β∣....(4.9)|(\boldsymbol{\alpha}, \boldsymbol{\beta})|=|(\boldsymbol{\alpha}, k \boldsymbol{\alpha})|=|k| \cdot|(\boldsymbol{\alpha}, \boldsymbol{\alpha})|=|k| \cdot|\boldsymbol{\alpha}|^2=|\boldsymbol{\alpha}| \cdot|\boldsymbol{\beta}| . ...(4.9)

若 α\boldsymbol{\alpha} 与 β\boldsymbol{\beta} 线性无关，则对任意实数 tt 都有 tα−β≠0t \boldsymbol{\alpha}-\boldsymbol{\beta} \neq \mathbf{0} ，从而

0<(tα−β,tα−β)=t2(α,α)−2t(α,β)+(β,β),...(4.10)0<(t \boldsymbol{\alpha}-\boldsymbol{\beta}, t \boldsymbol{\alpha}-\boldsymbol{\beta})=t^2(\boldsymbol{\alpha}, \boldsymbol{\alpha})-2 t(\boldsymbol{\alpha}, \boldsymbol{\beta})+(\boldsymbol{\beta}, \boldsymbol{\beta}), ...(4.10)

这是关于 tt 的一个二次三项式，由于对任意实数 tt ，式（4．10）都大于零，故其判别式

(2(α,β))2−4(α,α)⋅(β,β)<0,...(4.11)(2(\boldsymbol{\alpha}, \boldsymbol{\beta}))^2-4(\boldsymbol{\alpha}, \boldsymbol{\alpha}) \cdot(\boldsymbol{\beta}, \boldsymbol{\beta})<0, ...(4.11)

即得

∣(α,β)∣<∣α∣⋅∣β∣,\boxed{ |(\boldsymbol{\alpha}, \boldsymbol{\beta})|<|\boldsymbol{\alpha}| \cdot|\boldsymbol{\beta}|, }

从而即得定理．

由柯西－施瓦茨不等式可得到一系列重要不等式．

向量夹角

设 VV 为欧氏空间， α,β\boldsymbol{\alpha}, \boldsymbol{\beta} 为 VV 中的非零向量．令

⟨α,β⟩=arccos⁡(α,β)∣α∣⋅∣β∣,\langle\boldsymbol{\alpha}, \boldsymbol{\beta}\rangle=\arccos \frac{(\boldsymbol{\alpha}, \boldsymbol{\beta})}{|\boldsymbol{\alpha}| \cdot|\boldsymbol{\beta}|},

则称 ⟨α,β⟩\langle\boldsymbol{\alpha}, \boldsymbol{\beta}\rangle 为向量 α\boldsymbol{\alpha} 与 β\boldsymbol{\beta} 的夹角．特别地，当 (α,β)=0(\boldsymbol{\alpha}, \boldsymbol{\beta})=0 时称 α\boldsymbol{\alpha}与 β\boldsymbol{\beta} 正交，记作 α⊥β\boldsymbol{\alpha} \perp \boldsymbol{\beta} ．

零向量 0\mathbf{0} 可看作与 VV 中任意向量都正交．

正交向量组

设 α1,α2,⋯ ,αs\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_s 为欧氏空间 VV 中一组非零向量．若对任意 1⩽i,j⩽s1 \leqslant i, j \leqslant s ，当 i≠ji \neq j 时都有 αi⊥αj\boldsymbol{\alpha}_i \perp \boldsymbol{\alpha}_j ，则称向量组 α1,α2,⋯ ,αs\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_s为一个正交向量组．

例设 α1,α2\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2 是 Rn\mathbb{R}^n 中的非零向量，

β=α2−(α2,α1)(α1,α1)α1,\boldsymbol{\beta}=\boldsymbol{\alpha}_2-\frac{\left(\boldsymbol{\alpha}_2, \boldsymbol{\alpha}_1\right)}{\left(\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_1\right)} \boldsymbol{\alpha}_1,

证明：向量 α1\boldsymbol{\alpha}_1 和 β\boldsymbol{\beta} 正交． 证明：因为

(β,α1)=(α2−(α2,α1)(α1,α1)α1,α1)=(α2,α1)−(α2,α1)(α1,α1)(α1,α1)=0,\begin{aligned} \left(\boldsymbol{\beta}, \boldsymbol{\alpha}_1\right) & =\left(\boldsymbol{\alpha}_2-\frac{\left(\boldsymbol{\alpha}_2, \boldsymbol{\alpha}_1\right)}{\left(\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_1\right)} \boldsymbol{\alpha}_1, \boldsymbol{\alpha}_1\right) \\ & =\left(\boldsymbol{\alpha}_2, \boldsymbol{\alpha}_1\right)-\frac{\left(\boldsymbol{\alpha}_2, \boldsymbol{\alpha}_1\right)}{\left(\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_1\right)}\left(\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_1\right) \\ & =0, \end{aligned}

所以 α1\boldsymbol{\alpha}_1 与 β\boldsymbol{\beta} 正交．

距离

设 VV 为欧氏空间，对 α,β∈V\boldsymbol{\alpha}, \boldsymbol{\beta} \in V ，令

d(α,β)=∣α−β∣,d(\boldsymbol{\alpha}, \boldsymbol{\beta})=|\boldsymbol{\alpha}-\boldsymbol{\beta}|,

称 d(α,β)d(\boldsymbol{\alpha}, \boldsymbol{\beta}) 为向量 α\boldsymbol{\alpha} 与 β\boldsymbol{\beta} 的距离，即向量 α\boldsymbol{\alpha} 与 β\boldsymbol{\beta} 的距离等于向量 α−β\boldsymbol{\alpha}-\boldsymbol{\beta} 的长度．

前の章1._本章公式汇总
次の章3._向量的内积_长度
2._数学空间与欧氏空间 - 线性代数 | OpenTech