3._向量的内积_长度

向量的内积

在向量空间 里介绍了向量的加法和数乘等基本概念。而未顾及几何上的特性，例如长度和角度等概念．内积的概念就蕴含了这些几何层面的想法，它是我们本章研究的主题．

每种内积都可诱导出一种范数（你可以把范数看成长度）．范数满足一些重要的性质，例如毕达哥拉斯定理、三角不等式、平行四边形等式和柯西-施瓦兹不等式．在讨论内积空间时，我们将欧几里得几何中的垂直向量这一概念，重命名为正交向量．我们将看到，规范正交基在内积空间中非常有用．格拉姆-施密特过程可构造出这样的基．本章结尾处，我们将综合运用上述工具来解决最小化问题．

向量的内积的定义

设有 nn 维向量 x=(x1x2⋮xn),y=(y1y2⋮yn),\boldsymbol{x}=\left(\begin{array}{l}x_1 \\ x_2 \\ \vdots \\ x_n\end{array}\right), \boldsymbol{y}=\left(\begin{array}{l}y_1 \\ y_2 \\ \vdots \\ y_n\end{array}\right), \quad 令 [x,y]=xTy=x1y1+x2y2+⋯+xnyn[\boldsymbol{x}, \boldsymbol{y}]=\boldsymbol{x}^{\mathrm{T}} \boldsymbol{y}=x_1 y_1+x_2 y_2+\cdots+x_n y_n, 称 [x,y][\boldsymbol{x}, \boldsymbol{y}] 为向量 x\boldsymbol{x} 与 y\boldsymbol{y} 的内积.

注：向量内积就是对应坐标相乘后，再相加。另外，向量内积可以记做 (x,y)(\boldsymbol{x},\boldsymbol{y}) 或 [x,y][\boldsymbol{x},\boldsymbol{y}]， 而向量夹角记作 <x,y><\boldsymbol{x},\boldsymbol{y}> ，不同教程，记法略有差别 ,不同教程记法乱七八糟，我们也没办法，有时候都分不清到底是矩阵，是行列式，是绝对值，还是内积。

内积的性质 (其中 x,y\boldsymbol{x}, \boldsymbol{y} 与 z\boldsymbol{z} 都是 nn 维列向量， λ\lambda 为实数):

(i) [x,y]=[y,x][x, y]=[y, x]; (ii) [λx,y]=λ[x,y]=[x,λy][\lambda x, y]=\lambda[x, y]=[x, \lambda y]; (iii) [x+y,z]=[x,z]+[y,z][x+y, z]=[x, z]+[y, z]; (iv) [x,x]≥0[x, x] \geq 0 ，当且仅当 x=0\boldsymbol{x}=\mathbf{0} 时， [x,x]=0[\boldsymbol{x}, \boldsymbol{x}]=0. 利用这些性质，还可以证明著名的柯西-施瓦茨 不等式

[x,y]2≤[x,x][y,y].[x, y]^2 \leq[x, x][y, y] .

向量内积的几何意义

两个向量x,y\boldsymbol{x},\boldsymbol{y} 如果把他们的值看成空间里的坐标，则向量内积的定义就是他们对应坐标值相乘，或许我们为什么要问一下：为什么要这么定义他的内积呢？向量的内积本质上表示的是一个向量在另外一个向量上的投影。

我们以二维为例，通常认为，向量内积表示的一个向量在另外一个向量上的投影 ， 详见高中向量内积 这样，两个向量的乘法就变成：(这里|a|表示向量a的模长，|b|表示向量b的模长)

a⋅b=∣a∣∣b∣cosθ...①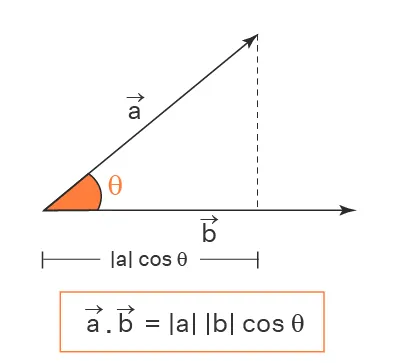\boxed{ a \cdot b =|a| |b| cos \theta ...① }

img-text

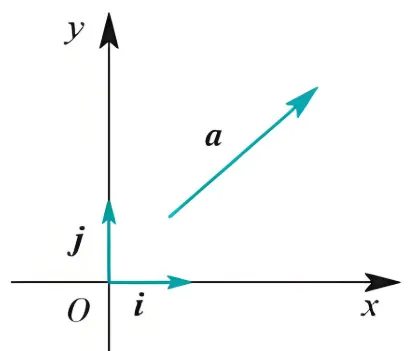
另一方面，假设每个向量用坐标轴表示

图片{width=300px}

给定两个坐标表示的向量 a⃗=(x1,y1)\vec{a}=\left(x_1, y_1\right) 与 b⃗=(x2,y2)\vec{b}=\left(x_2, y_2\right) ，它们的内积是

a⃗⋅b⃗=(x1i⃗+y1j⃗)⋅(x2i⃗+y2j⃗)=(x1x2)i⃗2+(x1y2+x2y1)i⃗⋅j⃗+y1y2j⃗2\begin{aligned} \vec{a} \cdot \vec{b} & =\left(x_1 \vec{i}+y_1 \vec{j}\right) \cdot\left(x_2 \vec{i}+y_2 \vec{j}\right) \\ & =\left(x_1 x_2\right) \vec{i}^2+\left(x_1 y_2+x_2 y_1\right) \vec{i} \cdot \vec{j}+y_1 y_2 \vec{j}^2 \end{aligned}

因为 i⃗、j⃗\vec{i} 、 \vec{j} 是互相垂直的单位向量，所以 i⃗2=1,i⃗⋅j⃗=0\vec{i}^2=1, \vec{i} \cdot \vec{j}=0 ， j⃗2=1\vec{j}^2=1 ，于是

a⃗⋅b⃗=x1x2+y1y2...②\boxed{ \vec{a} \cdot \vec{b}=x_1 x_2+y_1 y_2 ...② }

这就是说，两个向量的数量积等于它们对应坐标的乘积的和．

这样，我们看到两个向量的内积：

本质上是一个向量在另外一个向量上的投影，而他的计算方式可以直接用对应坐标值相乘后再相加。

把这个思想推广到nn维，就是上面的定义。

例

x=(−123),y=(103)\boldsymbol{x}=\left(\begin{array}{l}-1 \\ 2 \\ 3\end{array}\right), \boldsymbol{y}=\left(\begin{array}{l} 1 \\ 0 \\ 3 \end{array}\right)

根据定义，容易得到 [x,y]=−1∗1+2∗0+3∗3=8[x,y]=-1*1+2*0+3*3=8

向量的长度

设有 nn 维向量 x=(x1x2⋮xn)\boldsymbol{x}=\left(\begin{array}{l}x_1 \\ x_2 \\ \vdots \\ x_n\end{array}\right), ∥x∥=[x,x]=x12+x22+⋯+xn2\|\boldsymbol{x}\|=\sqrt{[\boldsymbol{x}, \boldsymbol{x}]}=\sqrt{x_1^2+x_2^2+\cdots+x_n^2}, 称 ∥x∥\|\boldsymbol{x}\| 为向量 x\boldsymbol{x} 的长度（或范数）.

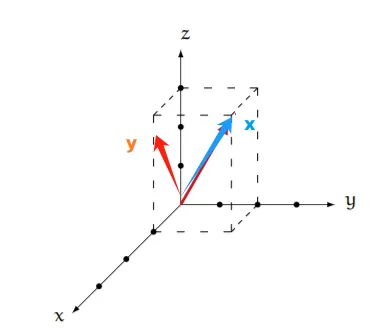
例 已知向量 x=(−123)\boldsymbol{x}=\left(\begin{array}{l}-1 \\ 2 \\ 3\end{array}\right) 求其长度。 解：如下图，根据空间坐标系知道u(−1,2,3)u(-1,2,3)， 根据勾股定理可以得到 ∣∣x∣∣=(−1)2+22+32=14||x||=\sqrt{(-1)^2+2^2+3^2}=\sqrt{14}

图片

向量的长度具有下述性质： (i) 非负性 当 x≠0x \neq 0 时， ∥x∥>0\|x\|>0 ；当 x=0x=0 时， ∥x∥=0\|x\|=0; (ii) 齐次性 ∥λx∣=∣λ∣⋅∥x∥\|\lambda x|=| \lambda \mid \cdot\| x \|; (iii) 三角不等式 ∥x+y∥≤∥x∥+∥y∥\|x+y\| \leq\|x\|+\|y\|. 证明: (i)与(ii)是显然的，下面证明(iii). 因为 ∥x+y∥2=[x+y,x+y]=[x,x]+2[x,y]+[y,y]\|x+y\|^2=[x+y, x+y]=[x, x]+2[x, y]+[y, y], 由施瓦茨不等式，有 [x,y]≤[x,x][y,y][x, y] \leq \sqrt{[x, x][y, y]}, 从而 ∥x+y∥2≤[x,x]+2[x,x][y,y]+[y,y]=∥x∥2+2∥x∥y∥+∥y∥2=(∥x∥+∥y∥2\quad\|\boldsymbol{x}+\boldsymbol{y}\|^2 \leq[\boldsymbol{x}, \boldsymbol{x}]+2 \sqrt{[\boldsymbol{x}, \boldsymbol{x}][\boldsymbol{y}, \boldsymbol{y}]}+[\boldsymbol{y}, \boldsymbol{y}]=\|\boldsymbol{x}\|^2+2\|\boldsymbol{x}\| \boldsymbol{y}\|+\| \boldsymbol{y} \|^2=\left(\|\boldsymbol{x}\|+\|\boldsymbol{y}\|^2\right., 即 ∥x+y∥≤∥x∥+∥y∥\|\boldsymbol{x}+\boldsymbol{y}\| \leq\|\boldsymbol{x}\|+\|\boldsymbol{y}\|.

向量的单位化

当 ∥x∥=1\|x\|=1 时，称 x\boldsymbol{x} 为单位向量. 如果 α≠0\boldsymbol{\alpha} \neq \mathbf{0} ，取 β=α∥α∥\beta=\frac{\alpha}{\|\alpha\|} ，则 β\beta 是一个单位向量. 由向量 α\alpha 得到单位向量 β\beta 的过程称为把向量 α\alpha 单位化.

例已知向量 x=(−123)\boldsymbol{x}=\left(\begin{array}{l}-1 \\ 2 \\ 3\end{array}\right) ，求其单位化。 解：由上面例题知道xx的长度为14\sqrt{14}， 所以，单位化后，向量为 β=(−114214314)\boldsymbol{\beta}=\left(\begin{array}{l} \frac{-1}{\sqrt{14}} \\ \frac{2}{\sqrt{14}} \\ \frac{3}{\sqrt{14}} \end{array}\right)

向量的夹角

由上面①②定义可以，①等于②，因此

cosθ=x1x2+y1y2cos \theta = x_1 x_2+y_1 y_2

所以，

cosθ=x1x2+y1y2∣a∣∣b∣cos \theta = \dfrac{ x_1 x_2+y_1 y_2 }{ |a| |b| }

当 x≠0,y≠0x \neq 0, y \neq 0 时，

θ=arccos⁡[x,y]∥x∥y∥\theta=\arccos \frac{[\boldsymbol{x}, \boldsymbol{y}]}{\|\boldsymbol{x}\| \boldsymbol{y} \|}

称为 nn 维向量x\boldsymbol{x} 与 y\boldsymbol{y} 的夹角

当 [x,y]=0[x, y]=0 时，称向量 xx 与 yy 正交.

显然，若 x=0\boldsymbol{x}=\boldsymbol{0} ，则 x\boldsymbol{x} 与任何向量都正交. 例 已知向量

x=(−123),y=(103)\boldsymbol{x}=\left(\begin{array}{l}-1 \\ 2 \\ 3\end{array}\right), \boldsymbol{y}=\left(\begin{array}{l} 1 \\ 0 \\ 3 \end{array}\right)

，求其夹角 解： 图片 ∣∣x∣∣||x||=(−1)2+22+32=14\sqrt{(-1)^2+2^2+3^2}=\sqrt{14} ∣∣y∣∣||y||=(1)2+02+32=10\sqrt{(1)^2+0^2+3^2}=\sqrt{10} [[x,y]=−1∗1+2∗0+3∗3=8[[x,y]=-1*1+2*0+3*3=8

所以夹角 θ=arccos⁡814∗10=arccos⁡235 \theta=\arccos \frac{8}{14*10}=\arccos \frac{2}{35}

例 已知 a=(3,−1),b=(1,−2)\boldsymbol{a}=(3,-1), \boldsymbol{b}=(1,-2), 求 a⋅b,∣a∣,∣b∣,⟨a,b⟩\boldsymbol{a} \cdot \boldsymbol{b},|\boldsymbol{a}|,|\boldsymbol{b}|,\langle\boldsymbol{a}, \boldsymbol{b}\rangle. 解 由题意可知

a⋅b=(3,−1)⋅(1,−2)=3×1+(−1)×(−2)=5,∣a∣=a⋅a=32+(−1)2=10,∣b∣=b⋅b=12+(−2)2=5.\begin{aligned} & \boldsymbol{a} \cdot \boldsymbol{b}=(3,-1) \cdot(1,-2)=3 \times 1+(-1) \times(-2)=5, \\ & |\boldsymbol{a}|=\sqrt{\boldsymbol{a} \cdot \boldsymbol{a}}=\sqrt{3^2+(-1)^2}=\sqrt{10}, \\ & |\boldsymbol{b}|=\sqrt{\boldsymbol{b} \cdot \boldsymbol{b}}=\sqrt{1^2+(-2)^2}=\sqrt{5} . \end{aligned}

又因为

cos⁡⟨a,b⟩=a⋅b∣a∣∣b∣=510×5=22\cos \langle\boldsymbol{a}, \boldsymbol{b}\rangle=\frac{\boldsymbol{a} \cdot \boldsymbol{b}}{|\boldsymbol{a}||\boldsymbol{b}|}=\frac{5}{\sqrt{10} \times \sqrt{5}}=\frac{\sqrt{2}}{2}

所以 两个向量的夹角为 ⟨a,b⟩=π4\langle a, b\rangle= \frac{\pi}{4}

方向角与方向角余弦

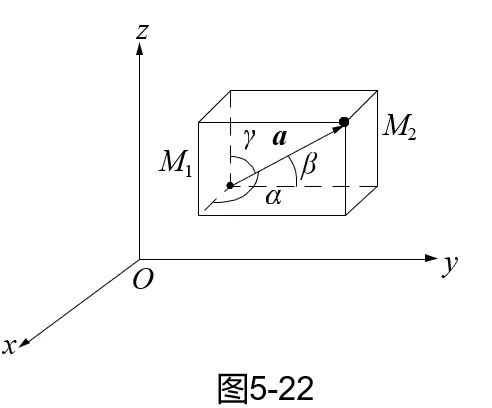
设 a\boldsymbol{a} 为任意一个向量，又设 α、β、γ\alpha 、 \beta 、 \gamma 为与三坐标轴正向之间的夹角 (0≤α,β,γ<π)(0 \leq \alpha, \beta, \gamma<\pi) ，如图 5-22 所示， α，β，γ\alpha ， \beta ， \gamma 分别为向量 a\boldsymbol{a} 的方向角. 由于向量坐标就是向量在坐标轴上的投影，故有

ax=∣a∣cos⁡α,ay=∣a∣cos⁡β，az=∣a∣cos⁡γ,a_x=|\boldsymbol{a}| \cos \alpha, \quad a_y=|\boldsymbol{a}| \cos \beta ， \quad a_z=|\boldsymbol{a}| \cos \gamma,

其中 cos⁡α、cos⁡β、cos⁡γ\cos \alpha 、 \cos \beta 、 \cos \gamma 称为向量 a\boldsymbol{a} 的方向余弦，通常用它表示向量的方向. 图片

由模的定义，可知向量 aa 的模为

∣a∣=(x2−x1)2+(y2−y1)2+(z2−z1)2=ax2+ay2+az2.|\boldsymbol{a}|=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2+\left(z_2-z_1\right)^2}=\sqrt{a_x^2+a_y^2+a_z^2} .

或 cos⁡α=axax2+ay2+az2...①,cos⁡β=ayax2+ay2+az2...②,cos⁡γ=azax2+ay2+az2...③\cos \alpha=\frac{a_x}{\sqrt{a_x^2+a_y^2+a_z^2}} ...①, \cos \beta=\frac{a_y}{\sqrt{a_x^2+a_y^2+a_z^2}}...②, \cos \gamma=\frac{a_z}{\sqrt{a_x^2+a_y^2+a_z^2}}...③,

①②③平方相加可得

cos⁡2α+cos⁡2β+cos⁡2γ=1，\boxed{ \cos ^2 \alpha+\cos ^2 \beta+\cos ^2 \gamma=1 ， }

即任一向量的方向余弦的平方和为 1 .

ea=a∣a∣=1∣a∣(ax,ay,az)=1ax2+ay2+az2(ax,ay,az)=(cos⁡α,cos⁡β,cos⁡γ).\boldsymbol{e}_a=\frac{\boldsymbol{a}}{|\boldsymbol{a}|}=\frac{1}{|\boldsymbol{a}|}\left(a_x, a_y, a_z\right)=\frac{1}{\sqrt{a_x^2+a_y^2+a_z^2}}\left(a_x, a_y, a_z\right)=(\cos \alpha, \cos \beta, \cos \gamma) .

要查看高中版请点击 空间向量方向角

例 设两已知点 M1(2,2,2)M_1(2,2, \sqrt{2}) 和 M2(1,3,0)M_2(1,3,0) ，分别写出向量 M1M2→、M2M1→\overrightarrow{M_1 M_2} 、 \overrightarrow{M_2 M_1} 的 坐标表达式和向表达式，计算它们的模、方向余弦、方向角、单位向量. 解 向量 M1M2→=(1−2,3−2,0−2)=(−1,1,−2)=−i+j−2k\overrightarrow{M_1 M_2}=(1-2,3-2,0-\sqrt{2})=(-1,1,-\sqrt{2})=-\boldsymbol{i}+\boldsymbol{j}-\sqrt{2} \boldsymbol{k} ，

M2M1→=−M1M2→=−(−1,1,−2)=(1,−1,2)=i−j+2k\overrightarrow{M_2 M_1}=-\overrightarrow{M_1 M_2}=-(-1,1,-\sqrt{2})=(1,-1, \sqrt{2})=\boldsymbol{i}-\boldsymbol{j}+\sqrt{2} \boldsymbol{k}

模 ∣M1M2→∣=∣M2M1→∣=(−1)2+12+(−2)2=2\left|\overrightarrow{M_1 M_2}\right|=\left|\overrightarrow{M_2 M_1}\right|=\sqrt{(-1)^2+1^2+(-\sqrt{2})^2}=2 ， M1M2→\overrightarrow{M_1 M_2} 的方向余弦为

cos⁡α1=−12,cos⁡β1=12,cos⁡γ1=−22\cos \alpha_1=-\frac{1}{2}, \quad \cos \beta_1=\frac{1}{2}, \quad \cos \gamma_1=-\frac{\sqrt{2}}{2}

对应的方向角为

α1=23π，β1=13π，γ1=34π；\alpha_1=\frac{2}{3} \pi ， \quad \beta_1=\frac{1}{3} \pi ， \gamma_1=\frac{3}{4} \pi ；

同理可得 M2M1→\overrightarrow{M_2 M_1} 的方向余弦为

cos⁡α2=12,cos⁡β2=−12,cos⁡γ2=22 ； \cos \alpha_2=\frac{1}{2}, \quad \cos \beta_2=-\frac{1}{2}, \quad \cos \gamma_2=\frac{\sqrt{2}}{2} \text { ； }

对应的方向角为

α2=13π，β2=23π，γ2=14π ； \alpha_2=\frac{1}{3} \pi ， \quad \beta_2=\frac{2}{3} \pi ， \gamma_2=\frac{1}{4} \pi \text { ； }
M1M2→=(1−2,3−2,0−2)=(−1,1,−2)∣M1M2→∣=(−1)2+12+(−2)2=4=2 ， 故 \begin{aligned} & \overrightarrow{M_1 M_2}=(1-2,3-2,0-\sqrt{2})=(-1,1,-\sqrt{2}) \\ & \left|\overrightarrow{M_1 M_2}\right|=\sqrt{(-1)^2+1^2+(-\sqrt{2})^2}=\sqrt{4}=2 \text { ， 故 } \end{aligned}

与 M1M2→\overrightarrow{M_1 M_2} 同向的单位向量为 eM1M2=(−12,12,−22)\boldsymbol{e}_{M_1 M_2}=\left(-\frac{1}{2}, \frac{1}{2},-\frac{\sqrt{2}}{2}\right), 与 M⃗2M1\vec{M}_2 M_1 同向的单位向量为 eM2M1=(12,−12,22)\boldsymbol{e}_{M_2 M_1}=\left(\frac{1}{2},-\frac{1}{2}, \frac{\sqrt{2}}{2}\right).

前の章2._数学空间与欧氏空间
次の章4._向量的外积
3._向量的内积_长度 - 线性代数 | OpenTech