向量减法
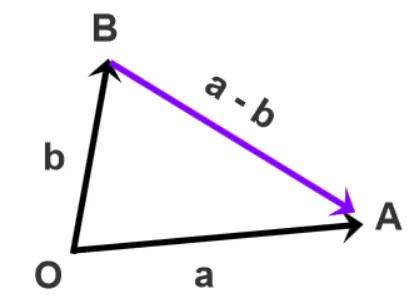
在理解施密特正交化之前,还是回顾一下向量减法。在高中介绍过向量的三角形法则, a−b=a+(−b), 表示如下,也就是向量减法里,向量的起点是B,终点是A, 即由B指向A, 详见 向量加减
 {width=200px}
记住这个结论,稍后将会用到。
{width=200px}
记住这个结论,稍后将会用到。
重要 在学习本文前务必理解了本章前面已经介绍的向量投影
施密特正交化简单解释
假设有两个线性无关的向量 a 和 b, 现在标准正交化这两个向量,让它们变成互相垂直的 q1 和 q2 。 所谓向量正交化就是找到一组垂直的向量 q1 和 q2,使得他们可以很容易的表示出a和b.
在理解正交化之前,我们举一个小例子:假设你是老师,要寻找班级里身高最高的学生,你会怎么做?你会让学生排成一排,然后从第一个学生开始,你默认他是班级里最高的,然后用第二个学生和第一个学生比较,如果第二个比第一个高,则交换他们的位置,否则,保持位置不变。 然后用第三个人还和“第一个”人比较,如果第三个人比第一个人高,则交换他们的位置,否则,保持不变,以此类推,最终,“第一个”人就是班级里最高的。施密特正交化的思想和此类似,给你一组向量,要找到一组互相垂直的向量,那我随便选一个作为基准,后续向量和他垂直即可。
现在有两个向量a,b,首先保持 a 不变让向量 A=a ,接下来要寻找到另一个向量 B ,使得 A⊥B (参考下图) 。假设B已经找到,容易看到p 是 b 在 a 上的投影, 根据上面介绍的向量的三角形减法法则,B 就相当于b−p
接下来的工作是看看B怎么用a,b来表示。
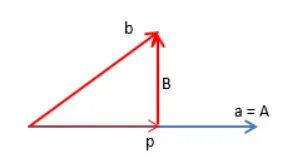
p 相当于 a 放缩了 x 倍,在一维空间内, x 是一个标量,可以表示为 (参考内积):
x=aTaaTbp=xa=aTaaTbxa∴B=b−p=b−aTaaTbxa 这相当于 B 是 b 减去 b 在 a 上的投影.
最后将 A 变成指向 A 方向的单位向量, B 变成指向 B 方向的单位向量:
q1=∥A∥A,q2=∥B∥B 这就是格拉姆-施密特正交化方法。
简单举例
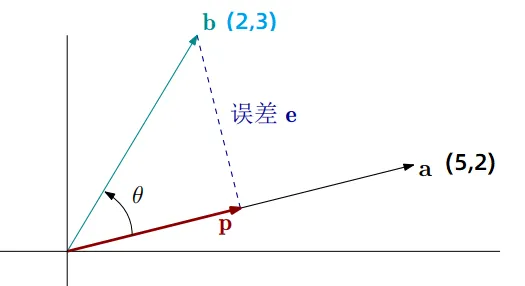
假设有两个向量: a=[52] 和 b=[23]
 {width=350px}
{width=350px}
仿照上面的步骤,看看怎么把他们正交化,我们必须时刻记着我们的目的是什么:找两个向量A,B,他们模长为1,且互相垂直。
所以,对于A直接使用a即可,即A=[52]
可以看到,对于A还是非常好找的,直接令A=a即可。
接下来找B,我们先计算一下 x=aTaaTb
因为两个向量内积,为两个向量坐标分量直接乘积,所以,
aTb=[5,2]∗[23]=16 aTa=[5,2]∗[52]=29 所以x=2916
所以 p=xa=2916(5,2)=(2980,2932)
因此B=b−p=[23]−[29802932]=[29−222955]
这样,我们就找到了一组互相垂直的向量A,B,即
A=[52] B=[29−222955] 单位化
上面找到的A,B是互相垂直的向量,但是我们还要向量的模长为1,所以需要把A,B单位化(单位化见此处)。
∣∣A∣∣=52+22=29
q1=[295292] ∣∣B∣∣=291129 ,所以
q2=291[−25] 这样 q1,q2 就是我们找到的正交向量组。
施密特正交化定义
设 α1,α2,⋯,αr 是向量空间 V 的一个基,从基 α1,α,⋯,αr 出发,找一组两两正交的单位向量, ξ1,ξ2,⋯,ξr, 使 ξ1,ξ2,⋯,ξr 与 α1,α2,⋯,αr 等价, 这个过程称为把基 α1,α2,⋯,αr 规范正交化.
具体步骤如下:
第一步,将基 α1,α2,⋯,αr 正交化 (施密特 (Schmidt) 正交化过程) .
β1=α1,β2=α2−[β1,β1][α2,β1]β1,β3=α3−[β1,β1][α3,β1]β1−[β2,β2][α3,β2]β2, 第二步,将 β1,β2,⋯,βr 单位化,得到 ξ1=∥β1∥1β1,ξ2=∥β2∥1β2,⋯,ξr=∥βr∥1βr
于是, ξ1,ξ2,⋯,ξ2 就是 V 的一个规范正交基.
上面计算里,[β1,α2] 表示 向量β1,α2的内积(见下面例题)[β1,β1] 表示 β1和自己的内积,即模长的平方。
记忆方法
施密特对角化看起来很复杂,但是有规律可循,假设给你四个向量α1,α2,α3,α4 要用施密特正交化找到四个向量 β1,β2,β3,β4 可以参考下面视频:(视频来B站自宋浩《线性代数》教材)
例 设 α1=11−1,α2=041,α3=−211 是 R3 的一个基,求一个与 α1,α2,α3 等价的规范正交基.
解 取
β1=α1=11−1,β2=α2−[β1,β1][β1,α2]β1=041−3311−1=−132,β3=α3−[β1,β1][β1,α3]β1−[β2,β2][β2,α3]β2=−211−3211−1−147−132=−6561−32, 再将 β1,β2,β3 单位化,得到 ξ1=∥β1∥1β1=3111−1,ξ2=∥β2∥1β2=141−132,ξ3=∥β3∥1β3=421−51−4, ξ1,ξ2,ξ3 即为所求.
在上面计算里,[β1,α2]=1∗0+1∗4+(−1)∗1=3 (即坐标对应乘积之和)
[β1,β1]=12+12+12=3 (即坐标平方之和)
上面是教材上常给的定义,但是很少进行解释。下面对上面进行几何解释。
如何理解施密特(Schmidt)正交化
为什么要使用施密特正交化法
在一个平面,或者三维空间中,任意一点都可以被坐标系表示出来。而我们更喜欢的是单位直角坐标系,因为在一个单位直角坐标系中,任意一个向量的坐标分量,通过简单的投影就可以搞定。
虽然我们喜欢用笛卡尔坐标系,但是其实任何模长为1切互相垂直的向量都可以坐标系。
因此,如何找到欧式空间的一个“直角坐标系”,变得非常重要。施密特正交化法就告诉我们了一种把“任意坐标系”变为“直角坐标系”的方法。
利用这个投影公式,我们便可以轻松理解施密特正交化法。如果您还未理解向量投影,请点击向量投影此处
我们首先需要理解一个向量 α2 在另外一个向量 α1 的投影公式。只要利用正交的定义,就很容易知道 α2 在 α1 的投影向量为
(α1,α1)(α2,α1)α1 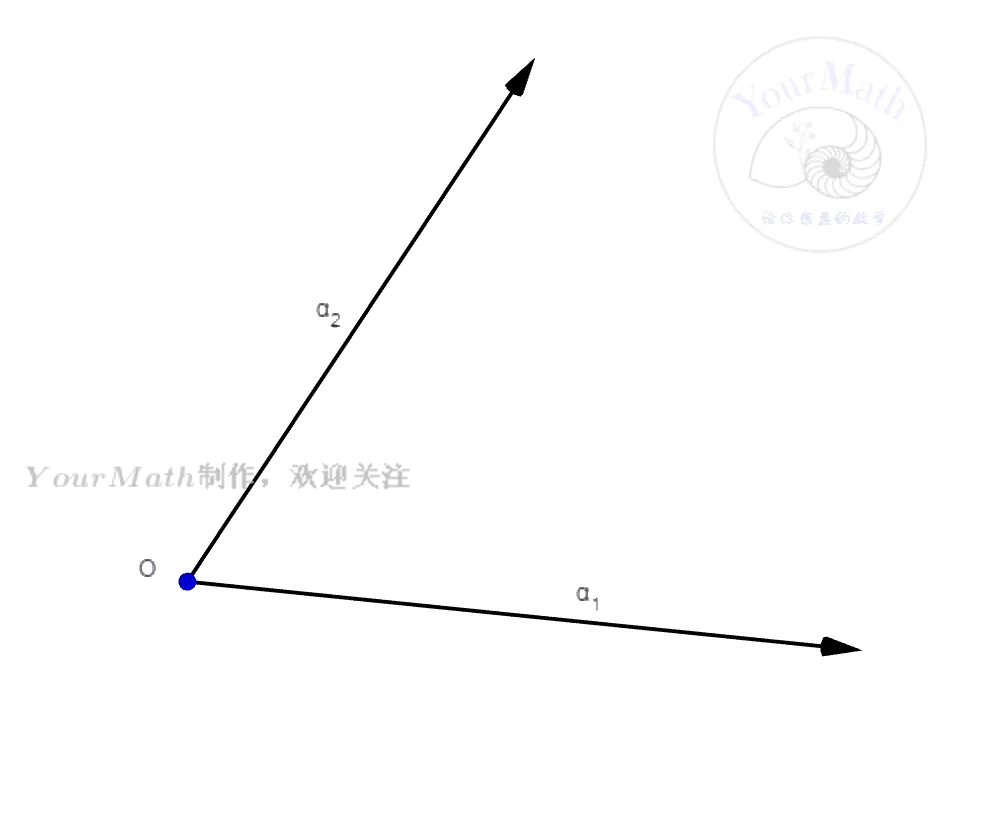 {width=450px}
{width=450px}
二维空间施密特正交化
平面上任意两个不共线的向量都可以构成平面的一个坐标系(也就是一组基),我们可以利用这两个向量之间的投影得到两个正交的向量:
Step1: 令 β1=α1
Step2: 做向量 α2 在向量 β1=α1 的投影,并与 α2 做差得到
β2=α2−(β1,β1)(β1,α2)β1 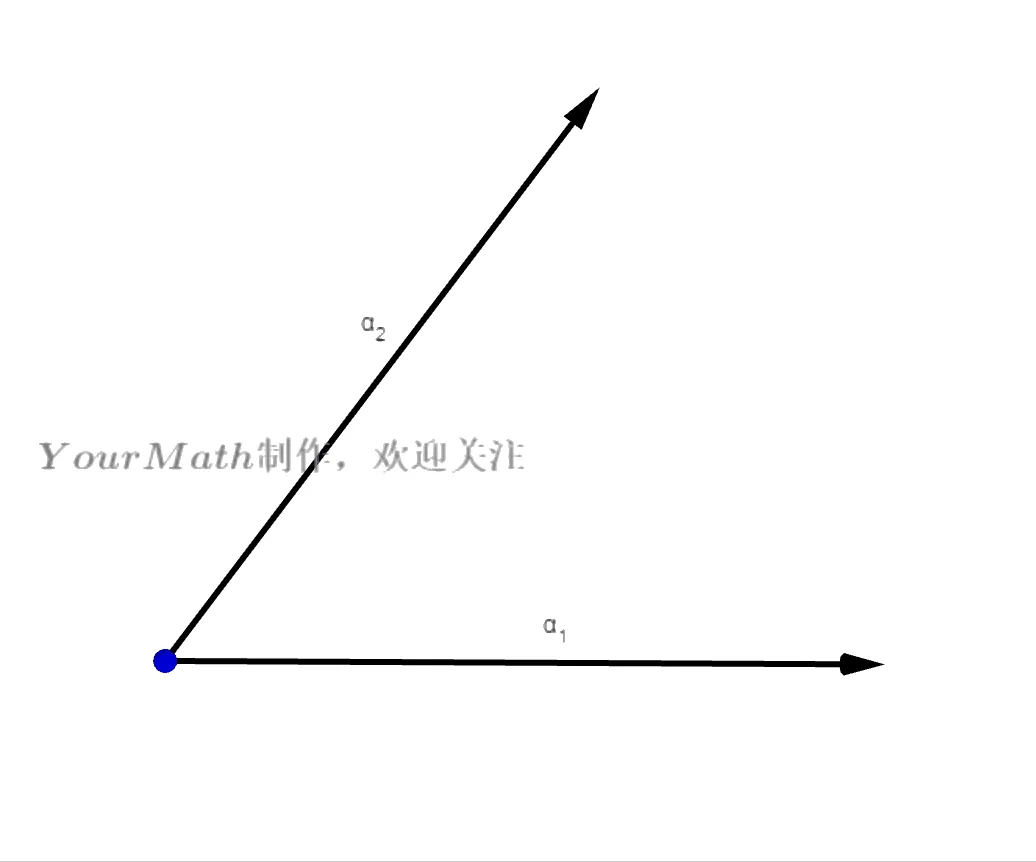
三维空间施密特正交化
对于一个三维欧空间来说, 我们看看如何利用施密特正交化法将这一组基正交化。
Step1: 令 β1=α1
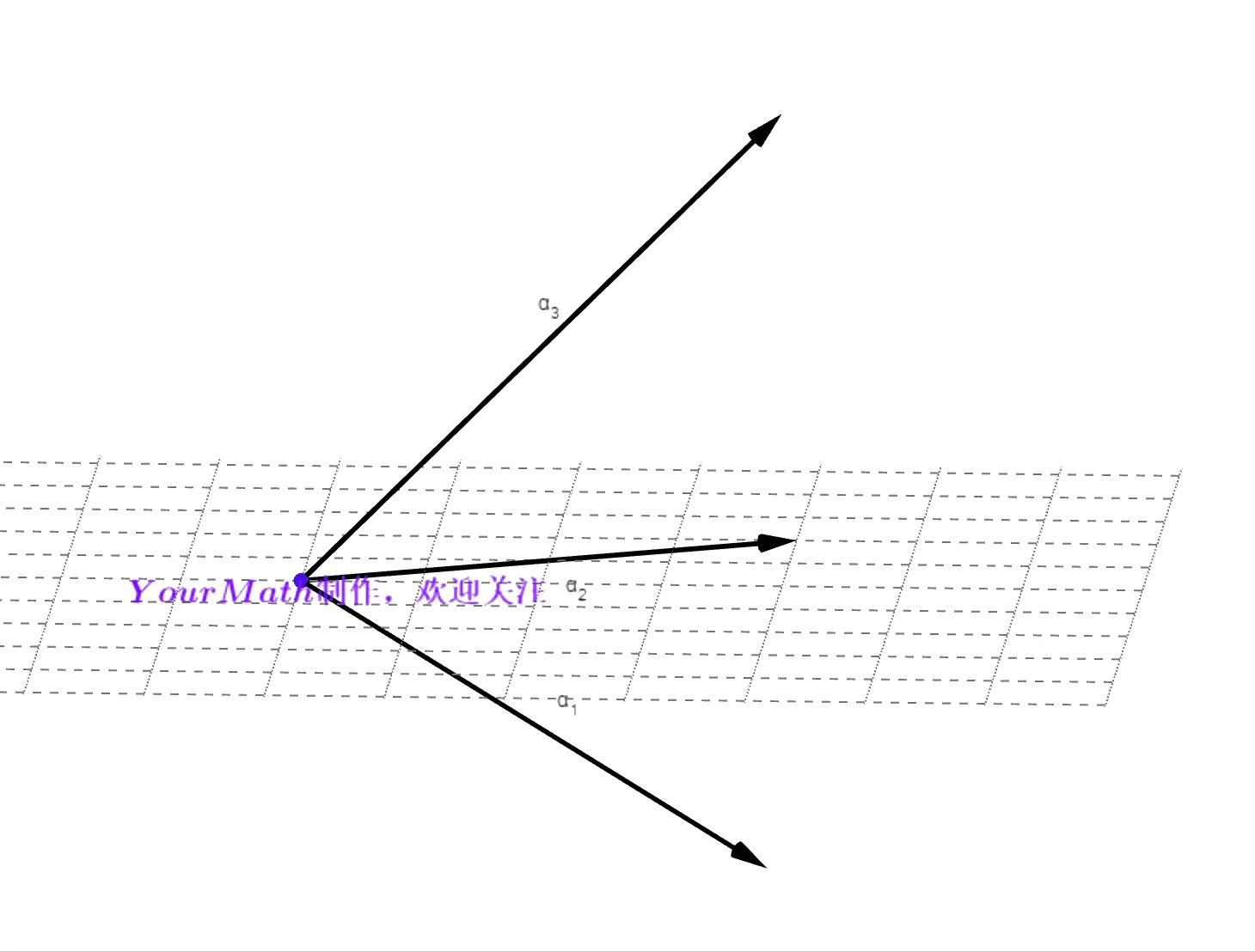
Step2:做向量α2 在向量 β1=α1 的投影,并与 α2 做差得到
β2=α2−(β1,β1)(α2,β1)β1:
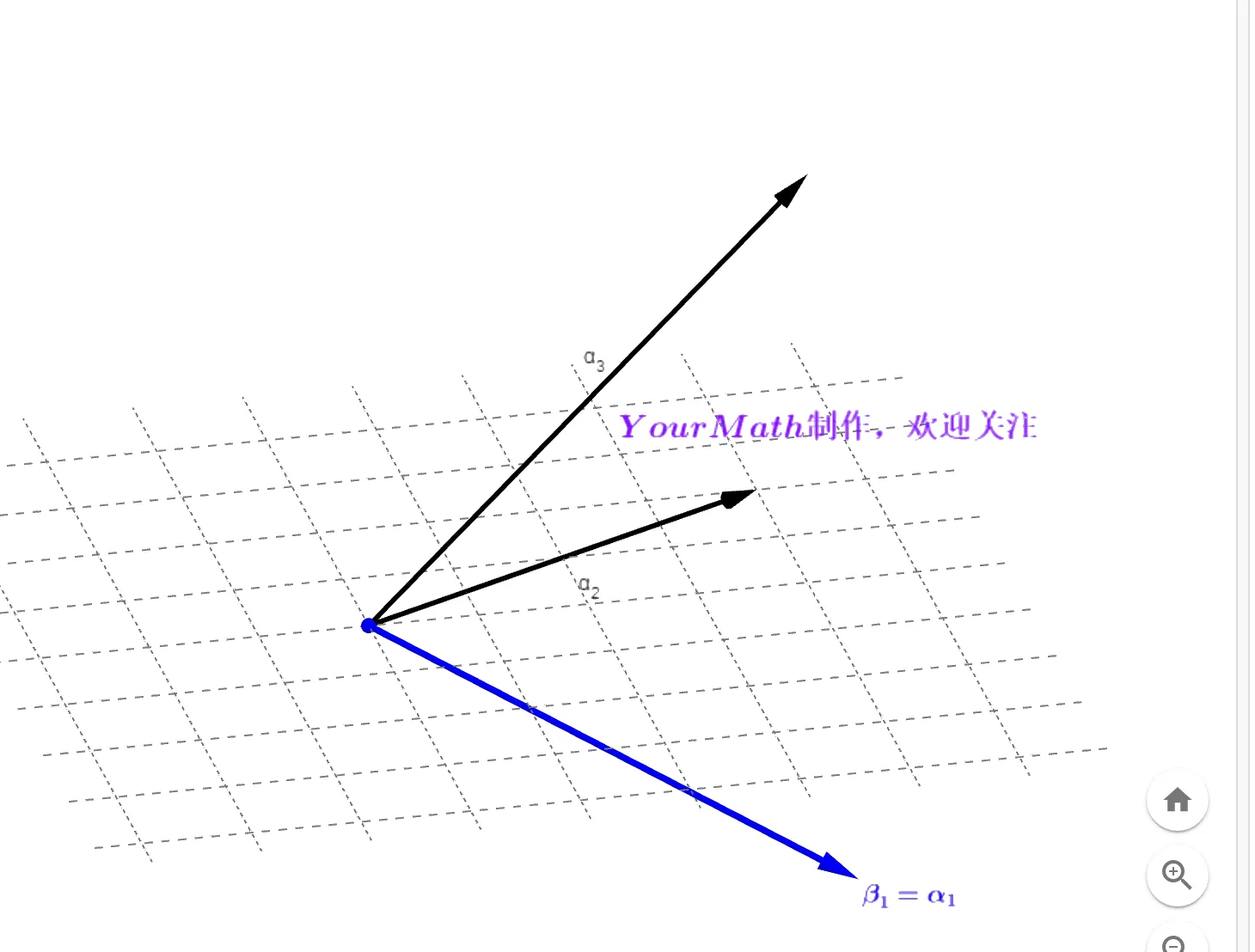
Step3: 分别做向量 α3 在向量 β1,β2 的投影 (β1,β1)(β1,α3)β1,(β2,β2)(β2,α3)β2 ,利用 α3 减去两个投影的和得到
β3=α3−(β1,β1)(β1,α3)β1−(β2,β2)(β2,α3)β2 请仔细观察下图理解。
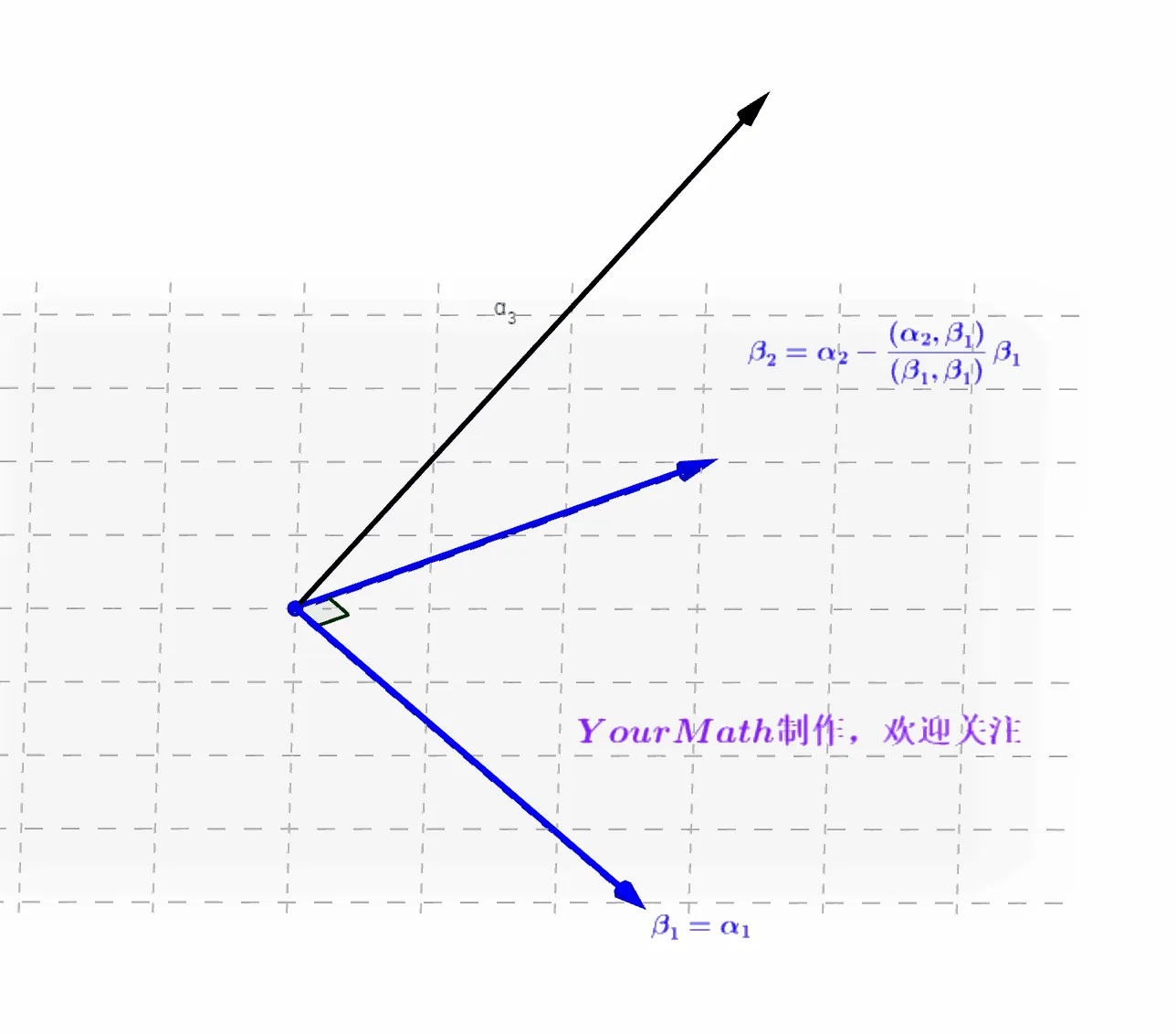
对于n维空间,和2维,3维类似。
下一节将给出具体例题,看过例题后,再来回顾本文介绍的内容。
 {width=200px}
记住这个结论,稍后将会用到。
{width=200px}
记住这个结论,稍后将会用到。
 {width=350px}
{width=350px} {width=450px}
{width=450px}


