8._向量正交

向量正交

向量正交是指：若两个同维向量 $\vec{u}, \vec{v}$ 的点乘（也叫：数量积）为 0 ，则两个向量正交（也叫：垂直），

上面做法用口诀记忆就是：两个向量内积为零则正交，反之，如果正交则内积为零。

理解：向量正交

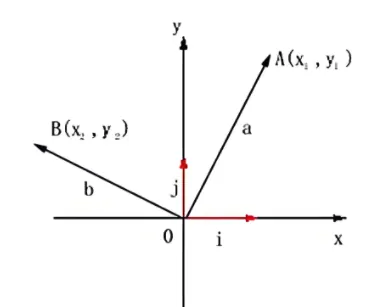
在二维平面里，我们有平面笛卡尔直角坐标系$i=(1,0), j=(0,1)$（也就是传统的x轴与y轴），很明显他们是正交的 {width=300px}

但是他们并不是唯一的，比如$a=(1,1)$ 和 $b=(1,-1)$也正交。

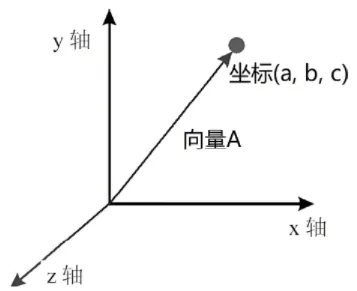
在三维空间里，也有空间笛卡尔坐标系$i=(1,0,0), j=(0,1,0),k=(0,0,1)$, （也就是传统的x轴，y轴与z轴） {width=300px}

例 验证向量 $u = (1, 2, 3)$ 和 $v = (7, 2, -11/3)$ 也是正交的。

解：计算点积

因为点积为 0，所以向量u 和 v 在三维空间中正交(互相垂直)。

现在的问题来了：给一组向量，如何快速找到一组相互垂直的坐标系（基），这就是接下来我们要研究的问题, 为此先给出正交向量组的概念。

正交向量组

定义 由一组两两正交的非零向量组成的向量组，称为正交向量组.

判定 若 $\alpha \beta =0$ 则称$\alpha$和$\beta$正交。

例

解：要判断$a,b,c$是正交向量组，就是要判断$ab=0,ac=0,bc=0$.

计算 $a \ b= 1*0+0*2+0*0=0$ 所以 $a,b$垂直，同样$b,c$,$a,c$ 都互相垂直。所以$a,b,c$构成一个正交向量组。

例 不难证明，下面四个向量也构造一个正交向量组。

从上面计算可以看出，两个向量正交，则对应坐标点相加为零。反正，如果对应坐标点相加为零，则两个向量正交，这是一个非常有用的结论。

定理1

若 $n$ 维向量组 $\alpha_1, \alpha_2, \cdots, \alpha_n$ 是一个正交向量组，则 $\alpha_1, \alpha_2, \cdots, \alpha_m$ 线性无关.

证明： 设有常数 $\lambda_1, \lambda_2, \cdots, \lambda_m$ ，使

以 $\boldsymbol{\alpha}_i^{\mathrm{T}}(i=1,2, \cdots, m)$ 左乘上式两端，当 $j \neq i$ 时， $\alpha_i^{\top} \boldsymbol{\alpha}_j=0$ ，从而有 $\lambda_i \boldsymbol{\alpha}_i^{\mathrm{T}} \boldsymbol{\alpha}_i=0(i=1,2, \cdots, m)$, 因 $\boldsymbol{\alpha}_i \neq \mathbf{0}(i=1,2, \cdots, m)$ ，故 $\alpha_i^{\mathrm{T}} \boldsymbol{\alpha}_i \neq 0$ ， 于是必有 $\lambda_i=0(i=1,2, \cdots, m)$ ，所以向量组 $\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_m$ 线性无关.

例 已知 3 维空间中的两个向量 $\alpha _1=\left(\begin{array}{c}1 \\ -1 \\ -1\end{array}\right), \alpha _2=\left(\begin{array}{c}1 \\ 2 \\ -1\end{array}\right)$ 正交，试求一个非零向量 $\alpha _3$ ，使 $\alpha _1, \alpha _2, \alpha _3$两两正交.

解：方法一：记

$\alpha _3$ 应满足齐次线性方程组 $A x = 0$ ，即 $\left(\begin{array}{ccc}1 & -1 & -1 \\ 1 & 2 & -1\end{array}\right)\left(\begin{array}{l}x_1 \\ x_2 \\ x_3\end{array}\right)=\binom{0}{0} ...(1)$, 对系数矩阵 $A$ 实施初等行变换，有 $A =\left(\begin{array}{ccc}1 & -1 & -1 \\ 1 & 2 & -1\end{array}\right) \rightarrow\left(\begin{array}{ccc}1 & -1 & -1 \\ 0 & 3 & 0\end{array}\right) \rightarrow\left(\begin{array}{ccc}1 & 0 & -1 \\ 0 & 1 & 0\end{array}\right)$,

得

从而有基础解系

取 $\alpha _3=\left(\begin{array}{l}1 \\ 0 \\ 1\end{array}\right)$ ，则 $\alpha _3$ 为所求.

解法2：既然互相垂直，自然 $\alpha_1 \alpha_3=0$ 和 $\alpha_2 \alpha_3=0$ 这样就可以得到两个方程组，即

解这个方程组即可，不过如果你仔细观察，上面这个方程写成矩阵的形式就是方法一的（1）式，所以两个过程本质是一样的，具体略。

规范正交基

设 $n$ 维向量组 $\xi_1, \xi_2, \cdots, \xi_r$ 是向量空间 $V\left(V \subseteq \mathbf{R}^n\right)$ 的一个基，如果 $\xi_1, \xi_2, \cdots, \xi_r$ 两两正交， 且都是单位向量， 则称 $\xi_1, \xi_2, \cdots, \xi_r$ 是 $v$ 的一个规范正交基. 例如， $n$ 维单位坐标向量 $e_1, e_2, \cdots, e_n$ 就是 $\mathbf{R}^n$ 的一个规范正交基. 向量组

就是 $\mathbf{R}^3$ 的一个规范正交基. 若 $\xi_1, \xi_2, \cdots, \xi_r$ 是 $V$ 的一个规范正交基， 那么 $V$ 中任一向量 $\beta$ 都能由 $\xi_1, \xi_2, \cdots, \xi_r$ 线性表示， 设表示式为

用 $\xi_i^{\mathrm{T}}(i=1, \cdots, r)$ 左乘上式，有 $\xi_i^{\mathrm{T}} \boldsymbol{\beta}=\lambda_i \xi_i^{\mathrm{T}} \xi_i=\lambda_i(i=1, \cdots, r)$, 即 $\lambda_i=\xi_i^{\mathrm{T}} \boldsymbol{\beta}=\left[\xi_i, \boldsymbol{\beta}\right](i=1, \cdots, r)$.

延伸阅读向量的正交

在二维平面上，有二维笛卡尔坐标系，即$e_1=(1,0),e_2={0,1}$ ，这两个向量互相垂直的充要条件是内积为零，即$e_1 \cdot e_2=1*0+0*1=0$ ，其推导可以参考向量正交

这个结论可以推广到三维、四维、一直到$n$维，以三维为例 $e_1=(1,0,0), e_2=(0,1,0), e_3=(0,0,1)$ 计算他们的内积 可以发现 $e_1 \cdot e_2=0,e_1 \cdot e_3=0, e_2 \cdot e_3=0$ ，所以 $e_1,e_2,e_3$ 互相垂直，我们把两两互相垂直的向量称为正交向量。

对于四维及其以上维度，已经无法画图，但是上面的结论是一样的。

向量的正交给我们计算向量带来了方便，因为任何一个向量和正交向量做内积，就表示这个向量在该坐标轴上的投影（或者说分量。）

{WIDTH=350PX}

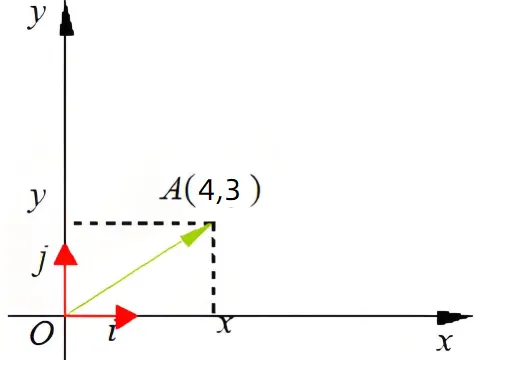
参考上图，比如有一个向量$\boldsymbol{a}=[4,3]$,我们要计算他在$\boldsymbol{e_1}$轴上的投影，可以计算 $a \cdot e_1=[4,3] \cdot [1,0]=4*1+3*0=4$ ，即向量在$x$轴分量为4.

同理， $a \cdot e_2=[4,3] \cdot [0,1]=4*0+3*1=3$ ，即向量在$y$轴分量为3.

这样，就把向量$[4,3]$ 分解为了2个向量：水平方向的$[4,0]$ 和 垂直方向上的 $[0,3]$，当处理向量时，直接使用分量进行处理。

因此，如果计算向量 $a+b$ 只要把他们的分量投影到对应的坐标轴上，然后对应的分量相加，即可得到向量的结果，这种分解的思想，相当于把向量运算转换为了分量上的代数式的加减，非常方便。

三角函数正交系

数学家们从向量的正交分解获得启发，提出了三角函数的正交性。 给你一个集合

我们称呼这个集合为三角函数系。 这里的$1$可以认为是$cos 0x$，而$0$是$sin0x$直接忽略没有再写。

在这个三角函数系里，任何两个函数沿着 $[-\pi, \pi]$ 积分（正好是一个周期），都可以得到他们的积分值为零。即

(1) $\int_{-\pi}^\pi \cos n x d x=0 , (n=1,2,3 \cdots)$

(2) $\int_{-\pi}^\pi \sin n x d x=0, (n=1,2,3, \cdots)$

(3) $\int_{-\pi}^\pi \sin k x \cdot \cos n x d x=0, (n, k=1,2,3 \cdots)$

(4) $\int$ $\int_{-\pi}^\pi \cos k x \cdot \cos n x, (n, k=1,2,3 \cdots, n \neq k)$

(5) $\int_{-\pi}^\pi \sin k x \cdot \sin n x d x=0, (n, k=1,2,3 \cdots, n \neq k)$

正如我们说两个向量点积为零则互相垂直一样，我们把两个三角函数在$[-\pi, \pi]$ 积分为零，称呼这2个三角函数正交。

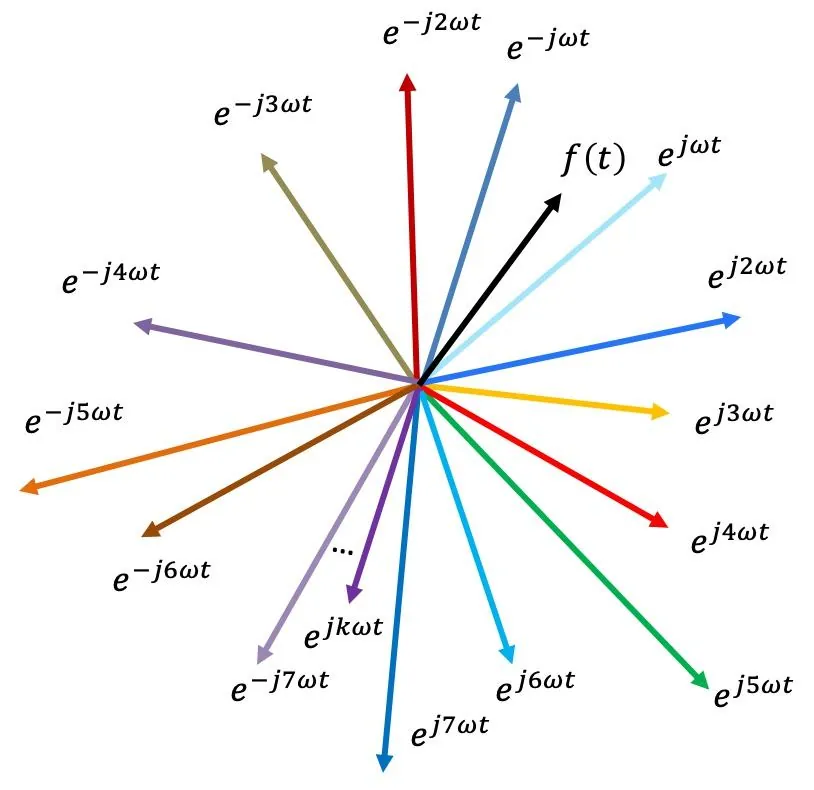
如果我们画出他的图形来，可以类似如下，注意：任何两个“函数”都互相垂直的(下图这里使用了复数表示)。

{width=500px}

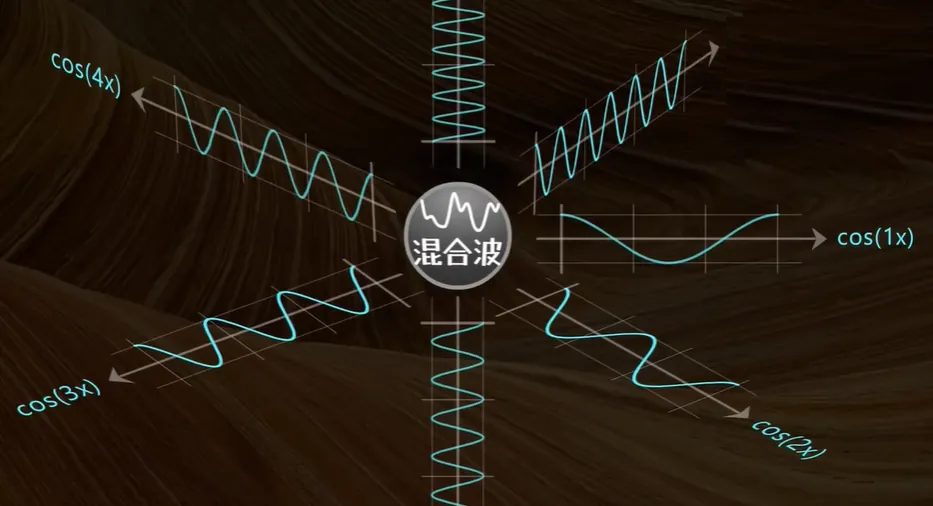
如果把上面图，进一步可视化，如下：会得到波的分解。

任何一个波，都可以分解到 三角函数正交系 上

{WIDTH=600PX}

但是光知道波的分解还不够，还需要知道波在该分量上的大小。再次回到向量，一个向量想知道他在每个基上的分量，只要用该向量和基单位做点积即可。同样的，

给你一个波只要和三角函数正交积做积分，就可以求得该分量的大小(振幅)。

这有什么用？ 想象你听了一段音乐，他的效果如下

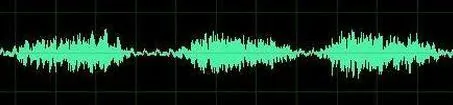
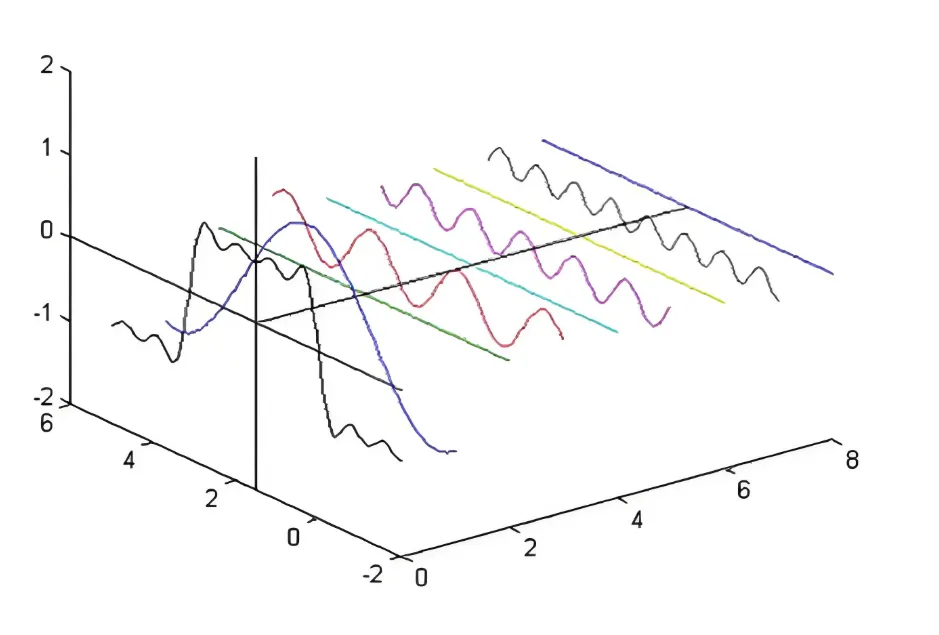
我们使用三角函数系和这段波“正交”（其实说过滤似乎更好），就可以得到各个不同频率三角函数的分量，这个通俗的理解是有一堆粮食，含有芝麻，大米，黄豆，西瓜等。我们拿一个筛子，从小到大，先使用芝麻的筛子，筛下来的都是芝麻，在使用大米筛子得到了大米，在用黄豆筛子得到了黄豆，最后是西瓜筛子，得到了西瓜。 比如原始声音函数$f(x)$ 就可以写成

这就是复数里的傅里叶变换。 {WIDTH=400PX}